Оглавление:


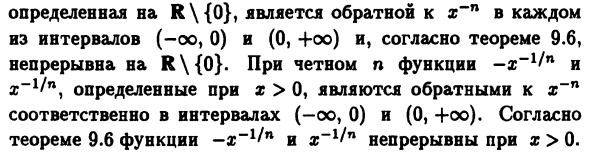

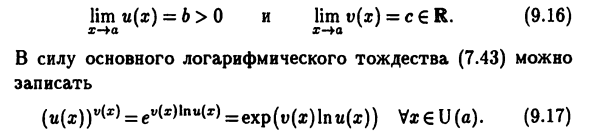

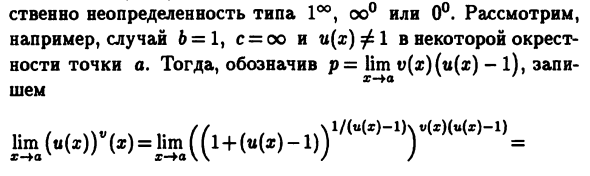
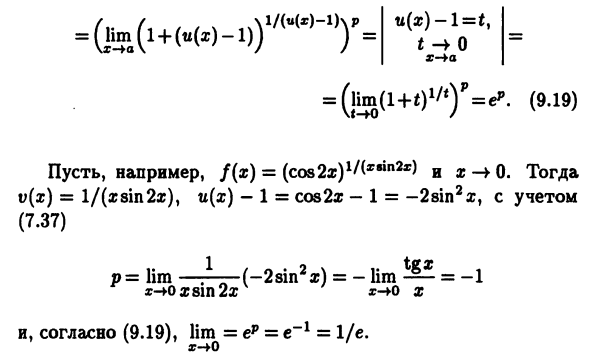

Непрерывность основных элементарных функций
- Примеры 9.1 и 9.2 устанавливают преемственность во всем Постоянная функция f (x) = c = число констант строки R Линейная функция x, тригонометрическая функция sin и: Экспоненциальная функция * функция. Как уже упоминалось в 9.2, из (7.25) Полиномы непрерывны всюду на R, а дробные рациональные числа Согласно (7.26) функция непрерывна во всех отношениях, кроме R. Те, чей знаменатель равен нулю. Пример 9.3 Непрерывность функции cos i везде установлена в R, а tanz Набор множеств {z∈R: xΦkn + nt / 2, k∈Z} и ctgx {x∈R: x for, k € Z}.
Теорема 9.6 означает непрерывность отрезка (0, + оо) Эти функции Противоположно друг другу, оно увеличивается, когда a> 1, и уменьшается, когда 0 0 и Строго монотонные функции -xlln и x1 / 71 Обратно на каждом из интервалов, показанных для функции xn Четное число n € N функции от x до n непрерывны в R \ {0}, x- »0 — бесконечно большая (bp) функция (в этом случае x = 0 По определению, функции являются вторым типом точки останова). Как и раньше, для нечетного n функция i «1/71, Каждый, определенный R \ {0}, является обратным к x ~ n.
Строго обратная логарифмическая функция logax Монотонный и непрерывный с экспоненциальной функцией R Диапазон значений (0, + оо). Людмила Фирмаль
Из интервалов (-oo, 0) и (0, + oo) согласно теореме 9.6 Непрерывно с R \ {0}. Для четного n функции от -x до 11n и x-1 / n, определенный для x> 0, является обратной величиной x ~ n. Через интервалы (-oo, 0) и (0, + oo) соответственно. По словам Согласно теореме 9.6 функции -x «» 1 / * и от x до 11n непрерывны с x> 0. Для рациональных чисел q = k / n € Q fc € Z, n € N (ib и n Неприводимо), функция xy непрерывна на месте Определение любым обобщением свойств (9.8) Степень функции xlnn или i «1/11. Обратные тригонометрические функции arcsinx и arccosx (См. Рисунки 3.19 и 3.20), согласно теореме 9.6, Сегмент [-1, 1], потому что функция фиксирует a. И еще: строго Монотонный и непрерывный на отрезке [-l- / 2, n / 2] соответственно А [0, tg] и их значения полностью заполняют интервал [-1, 1]. Функции arctgx и arcctgx (см. Рисунки 3.21 и 3.22),
еорема 9.6 утверждает, что функции tgx и ctgx строго Монотонный и непрерывный для x 6 (-mr / 2, mr / 2) И x € (0, l-), и их значения полностью заполняют целое число Direct R Поэтому все основные базовые функции Непрерывная функция класса, где бы она ни была определена Вы можете получить элемент, используя конечное число Основная элементарная алгебра Функции и их суперпозиция. Из свойств (9.7) — (9.9) Арифметические операции с использованием непрерывных функций и теорема 9.1 Непрерывность суперпозиции непрерывных функций Основная функция будет непрерывной в этом регионе Определение.
- Простейший пример базовой функции Полиномиальные и дробные рациональные функции. Пример 9.7. Рассмотрим функцию (ti (a :)) v. Где и (х) и v (x) — функция, определенная около U (a) Некоторые указывают на добавочный номер 6 R, а теперь Сосед u (x)> 0. Предположим, что существует Конечный предел lim u = 6> 0 и lim φ) = cK. (9,16) х- + а в х-ю С основным логарифмическим тождеством (7.43) вы можете: Запишите (I * ()) w (x) = ev lnttM = exp (φ) 1pi ()) V * € U (a). (9,17)Учитывая непрерывность логарифмической функции, (9.12) и (9.8), lim In и (x) = In (lim u (x)) = In 6, x- \ a v ‘\ x- * a v V lim v (x) \ nu (x) = lim v (x) • lim \ nu (x) = cln6. Следовательно, из-за непрерывности индекса (9.17) = 6 секунд (9,18)
Понятно, что u (x) и v (x) непрерывны в точках a и u (x)> > 0, функция (u (x)) v (x \ называется Экспоненциальный и непрерывный в каждой такой точке. Вы можете установить экспоненциальный лимит Не только условие (9.16). Когда вы можете найти lim v (x) \ nu (x) -d (конечный или бесконечный) известен. в Из последних d желаемый предел четко обозначен. если Если d = -co или d = + oo, целевой предел соответственно Ох или + оо. Возможно с заданными пределами b = lim u (x) и c = lim v (x) х- * а х- \ а Продукт v (x) \ nu (x) x- * a имеет тип 0 • oo неопределенность.
Само определение предела d является lim v (x) \ nu (x). х-ва Людмила Фирмаль
Легко установить этот исключительный случай Поддерживаются следующие комбинации b и c. 1) 6 = 1, с = оо. 2) 6 = + 00, s = 0; 3) 6 = c = 0. В этих случаях Формула (u (x)) v ^ x ‘при x-> a есть Поэтому такие неопределенности, как I00, co0, 0 °. рассматривать Например, случай 6 = 1, с = оо и и (х) ф \ Рядом. Далее p = lim v (x) (u (x) -l) Шем (U (x)) 1 ‘(a 🙂 = lim ((l + (tt (*) — l)) yK)’ т = u (x) -l = t, t- * O X- ¥ n = ep (9,19) Например, предположим, что f (x) = (ccn) 1 ^ * 8 «12 *) и a: -> 0. ) = 1 / (x8sh2ag), «(x) -1 = cos2a: -1 = -2sin2ar, принимая во внимание (7,37) p = lim ——-— (-2sin2a 🙂 = -lim — = — = -1 r> 0 X 81P 2x ar- + O X И согласно (9.19) lim = ep = e «1 = 1 / e.
Смотрите также:
| Односторонняя непрерывность. Точки разрыва | О вычислении нуля функции, непрерывной на отрезке |
| Свойства функций, непрерывных в промежутке | Сравнение бесконечно малых функций |
