Оглавление:

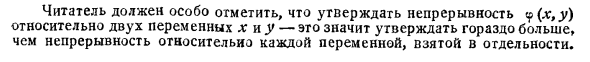




Непрерывные функции от нескольких переменных
- Непрерывная функция нескольких переменных. Понятие непрерывности и разрыва можно распространить на функции нескольких независимых переменных (см. Главу II, стр. 31). Однако применение этих функций связано с проблемами, которые намного сложнее, чем те, которые обсуждались в этой главе. Я не могу подробно остановиться на этих вопросах здесь, но я приведу здесь хорошее определение, потому что в будущем нам нужно знать, что означает непрерывная функция двух переменных. Это прямое обобщение формата последнего определения, описанного в разделе 99. Функция
i и y — * — m) Определение выглядит простым, но оно содержит фразы, которые еще не были уточнены в точном значении, и для того, чтобы прояснить его, нам нужно неравенство, подобное тому, которое содержится в основном утверждении. В сумме, произведении и общем случае легко доказать, что связь между непрерывными функциями двух переменных сама по себе непрерывна. Полиномы двух переменных непрерывны для всех значений этих переменных. Нормальные функции x и y, встречающиеся в анализе, также обычно непрерывны.
То есть все значения x и y являются непрерывными, кроме тех, которые связаны определенным отношением. Людмила Фирмаль
Читатель должен подчеркнуть, что они претендуют на непрерывность (x, y) по отношению к двум переменным x и y.Если (x, y) является непрерывным по отношению к x и y, ясно, что если y (или x) назначено фиксированное значение, оно является непрерывным по отношению к x (или y). Однако обратное никогда не бывает правдой. Например, / ч Если x или y равен нулю и x или y равен нулю,
> = 0. Значение x-0, y = 0 равно нулю, но x и строка y = ах, тогда 2а 2 Вы можете указать любое значение от -1 до 1. 109. Неявная функция. Ch II уже сталкивался с понятием неявных функций.
Следовательно, х н у y6-xy — y-x = 0, (1) у есть л: «Неявная функция *». Однако не ясно, что уравнение типа (1) фактически определяет функцию y из x или некоторую такую функцию. С ch II мы были рады видеть это как само собой разумеющееся. Теперь вы можете рассмотреть, было ли это предположение обоснованным. Следующие термины могут быть полезны в будущем: Предположим, вы можете построить квадрат вокруг точки (g, b), которая удовлетворяет определенным условиям, как в §108. Такой квадрат называется окрестностью (i, b), а указанное условие называется выполнением окрестности (a, b) или окрестности (a, b). Это позволяет легко найти квадрат, и это условие выполняется. Очевидно, что подобный термин может использоваться для функции одной переменной, если только квадраты заменяются линейным интервалом.
| Системы интервалов на прямой. Теорема Гейне — Бореля | Обратные функции |
| Колебание непрерывной функции | Производные или дифференциальные коэффициенты |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Теорема. Вели 1 ° f (x, y) является непрерывной функцией x и y в окрестности (a, e). T f (a, b) = 0, 3 ° f (x, y) для всех значений x в окрестности a является строго возрастающей функцией y (см. 95). Далее, (1) существует уникальная функция y = b (x). Подставляя в уравнение f (x, y) -0, то же самое верно для всех значений x в окрестности a. P.) o (.v) непрерывен для всех значений 0tq) x ecmH0cmu a. Квадраты на рисунке 1 32 представляют «соседей» (а, б). Условия 1 ° и 3 ° выполняются, и P является точкой (a, b). Как показано на рисунке, когда вы получаете точки 0 и β, f (x, y) является положительным для Q и отрицательным для R. Это так, и f (x.y) непрерывна в Q и β, поэтому мы можем нарисовать линии QQ ‘и RR’ параллельно OX. R’Q параллелен OY, а f (x, y) положительна и отрицательна в каждой точке QQ
RR ‘по всем параметрам. Эта конфигурация обеспечивает единственную точку, где f (x, y) = 0 на каждой ординате между RQ и R’Q. Также ясно, что такая конфигурация может быть выполнена на левой стороне RQ. y-u (lg). Осталось доказать, что φ (π) непрерывно. Это проще всего сделать, используя понятие верхнего и нижнего предела y (x) для a (см. §96). x- * a, где X и A — нижний и верхний пределы <p (x) для x — a соответственно.
В частности, поскольку f (x, y) положительно (отрицательно в R), оно исчезает только один раз в точке P ‘с R’Q \ на 3 ° и §101. Людмила Фирмаль
Очевидно, что точки (b, X) и (a, A) находятся на QR. Кроме того, вы можете найти последовательность значений x (*) -X как x — a, работающих значений этой последовательности, и Поскольку f {x, o (x)} = 0 и f {x, y) являются непрерывными функциями от x и y, f (a, X) = 0. Следовательно, X = b. Аналогично, A = b. Таким образом, <p (xr) ограничено b для x-a и непрерывно для x = a для (x). Очевидно, таким же образом мы можем показать непрерывность φ (π) для любого значения x вблизи a. Конечно, при условии 3 ° слово «увеличение» может быть заменено словом «уменьшение».
В качестве примера рассмотрим выражение (1), которое устанавливает q = 0 и £ = 0. Условия 1 ° и 2 ° явно выполняются. также • / (X, y) -фикс, Y) = (y- / Y (Y1 + Y * Y + N + YUn + Y * -X-; 1) Если x, y и y достаточно малы, они имеют противоположный знак — y. Следовательно, условие 3 ° («уменьшение», а не «увеличение») также выполняется. Если существует только одна непрерывная функция y, она полностью удовлетворяет уравнению (1) и 0, если * = 0. Тот же результат относится к уравнению у2-ху-у-х = 0. В этом случае функция у 0-0 ‘ р ‘ Кб) р R R ‘ Та же фигура. 32
Здесь подразумевается положительное значение маршрута. Второе значение маршрута с противоположным знаком не удовлетворяет условию равенства 0 при η = 0. В доказательстве есть один момент, на который следует обратить внимание. Гипотеза теоремы — это (a, b) окрестность i, то есть конкретный квадрат a-e r ^: x ^ a-e-, b-e e — {- e. Утверждение сделано «около x = a», то есть через равные промежутки времени a-e, ^ x ^ a — {- ej. Доказательство не указывает на то, что утверждение соответствует объекту e. Нет места. «
