Оглавление:
Неравенства и системы линейных неравенств с двумя переменными
Прямая на плоскости
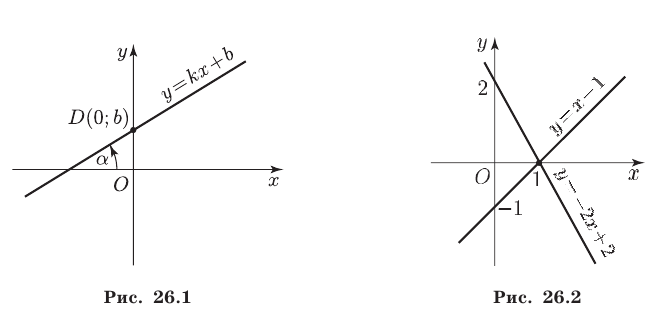
Пусть на плоскости задана прямоугольная система координат 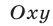 . Тогда уравнение
. Тогда уравнение
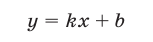
определяет прямую  (рис. 26.1), пересекающую ось
(рис. 26.1), пересекающую ось 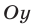 в точке
в точке 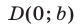 и образующую угол
и образующую угол 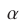 с положительным направлением оси
с положительным направлением оси 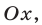 где
где 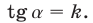 Число
Число 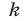 называют угловым коэффициен-том прямой
называют угловым коэффициен-том прямой 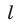 .
.
Если 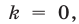 то прямая
то прямая 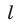 параллельна оси
параллельна оси 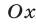 ; если
; если 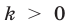 , то прямая
, то прямая 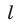 образует с осью
образует с осью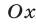 острый угол, а функция
острый угол, а функция 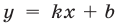 является возрастающей; если
является возрастающей; если 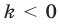 , то прямая
, то прямая 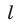 образует с осью
образует с осью 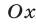 тупой угол, а функция
тупой угол, а функция 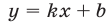 является убывающей.
является убывающей.
Для построения прямой 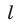 , заданной уравнением (1), достаточно найти две точки этой прямой. В качестве таких точек можно взять точки пересечения прямой
, заданной уравнением (1), достаточно найти две точки этой прямой. В качестве таких точек можно взять точки пересечения прямой 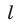 с осями координат.
с осями координат.
На рис. 26.2 изображены прямые, заданные уравнениями 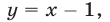
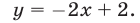
Рассмотрим уравнение
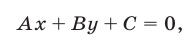
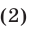
где хотя бы одно из чисел 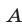 ,
,  не равно нулю. Если
не равно нулю. Если  , то уравнение (2) можно записать в виде
, то уравнение (2) можно записать в виде
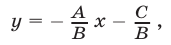
т. е. в виде (1), где 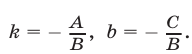
Следовательно, если 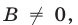 то уравнение (2) представляет собой уравнение прямой.
то уравнение (2) представляет собой уравнение прямой.
Если 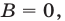 то уравнение (2) можно записать в виде
то уравнение (2) можно записать в виде
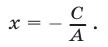
Это уравнение прямой, параллельной оси 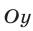 .
.
Таким образом, если 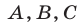 — заданные числа такие, что
— заданные числа такие, что 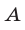 и
и  одновременно не равны нулю, то уравнение (2) является уравнением некоторой прямой.
одновременно не равны нулю, то уравнение (2) является уравнением некоторой прямой.
В случае, когда 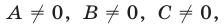 уравнение (2) можно записать так:
уравнение (2) можно записать так:
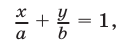
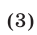
где 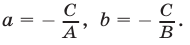
Уравнение (3) называется уравнением прямой в отрезках. Эта прямая пересекает ось 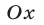 в точке
в точке 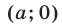 и ось
и ось 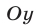 в точке
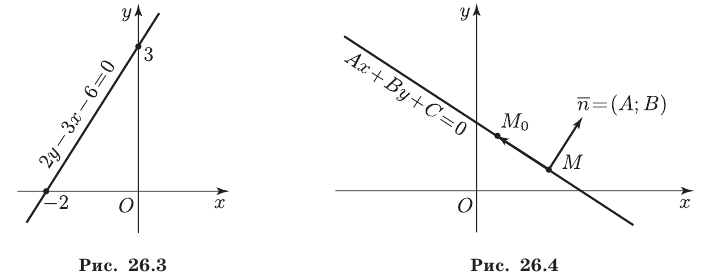
в точке 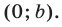 Например, уравнение
Например, уравнение
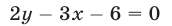
можно записать в виде 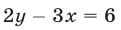 или в виде (3), т. е.
или в виде (3), т. е.
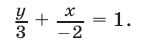
Эта прямая (рис. 26.3) проходит через точки 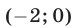 и
и 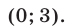 Если прямая
Если прямая  , заданная уравнением (2), проходит через точку
, заданная уравнением (2), проходит через точку 
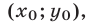 то
то
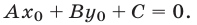
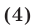
Вычитая из равенства (2) равенство (4), получаем
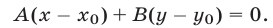
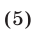
Левую часть равенства (5) можно рассматривать как скалярное произведение векторов 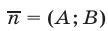 и
и 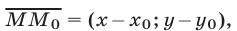 где
где 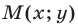 — произвольная точка прямой
— произвольная точка прямой 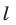 . Из (5) следует, что вектор
. Из (5) следует, что вектор 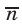 перпендикулярен прямой
перпендикулярен прямой 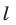 (рис. 26.4).
(рис. 26.4).
Угол между прямыми
Пусть прямые 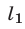 и
и 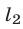 заданы соответственно уравнениями
заданы соответственно уравнениями
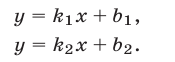
Если 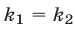 , то прямые
, то прямые 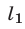 и
и 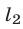 параллельны.
параллельны.
Пусть 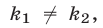 тогда прямые
тогда прямые 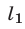 и
и 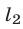 пересекаются в точке
пересекаются в точке 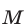 , координаты которой удовлетворяют системе (1), (2). Пересекающиеся прямые
, координаты которой удовлетворяют системе (1), (2). Пересекающиеся прямые 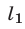 и
и 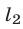 образуют две пары равных углов. Углом
образуют две пары равных углов. Углом 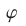 между прямыми
между прямыми 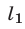 и
и 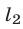 называют наименьший из этих углов. Если
называют наименьший из этих углов. Если 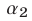 и
и 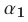 — углы, образуемые прямыми
— углы, образуемые прямыми 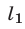 и
и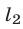 с осью
с осью 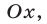 то
то 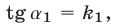
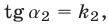 и поэтому
и поэтому
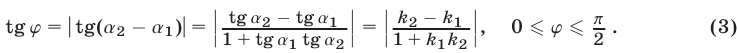
Если прямые 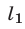 и
и 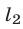 перпендикулярны и
перпендикулярны и 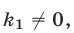 то
то 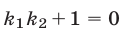 или
или
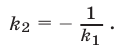
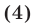
Если 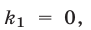 то
то 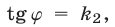 а прямой, которая перпендикулярна прямой
а прямой, которая перпендикулярна прямой 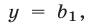 является любая прямая вида
является любая прямая вида 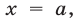 т. е. прямая, параллельная оси
т. е. прямая, параллельная оси 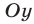 .
.
Пример №313.
Найти угол 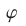 между прямыми
между прямыми 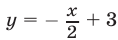 и
и 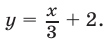
Решение:
По формуле (3), где 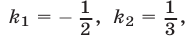 находим
находим
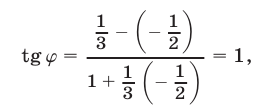
откуда 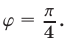
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
