Оглавление:








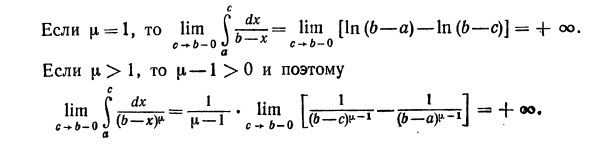




Несобственные интегралы
- Уникальный интеграл /. Интеграция с бесконечными границами Определение интегрирования, данное в § 2, было дано в предположении, что область интегрирования является конечным отрезком [a, b]. Предполагая, что область интегрирования бесконечна, например, в интервале [a, -foo), нормальное определение интегрирования не принимается даже для непрерывной функции f (x). В этом случае, если вы разделите интервал [a, -foo) на конечное число частей, одна из этих частей станет бесконечной, поэтому интегральная сумма не может быть объяснена.
Но прежде чем перейти к определению, рассмотрим пример. Функция = = непрерывна на бесконечном интервале [1, −∞). Таким образом, есть интеграл в сегменте [1, b] t, где 6> 1 J ** 1 b 9 1 b-> oo имеет предел, равный 1. Этот предел Вызывается неправильная интеграция функции ~ и показывает +00 JDX Вот так и ? , Im „t (l-iUl. Чтобы подвести итог этого примера, рассмотрим функцию y = f (x), которая непрерывна на бесконечных интервалах. б Существует интеграл J f (x) dx отрезка [a, b].
Здесь мы обобщаем понятие определенной интеграции в область бесконечной интеграции. Людмила Фирмаль
б , Интеграл <f (x;) dx идет до конечного предела но Неограниченное увеличение b, этот предел называется неправильным интегрированием с бесконечной верхней границей функции f (x) + » Обозначается символом J f (x) dx. но Вот так +00 i> $ f (x) dx = lim) f (x) dx. б- * + оо В этом случае несоответствующий интеграл J f (x) dx но Существует или сходится. Если указанный предел не существует (особенно если он бесконечен), они говорят, что интеграл не существует или расходится. Несоответствующие интегралы с бесконечной нижней границей определяются аналогично: б б $ f (x) dx = lim \ f (x) dx. + 00 (84) (83) а- * ■ -и
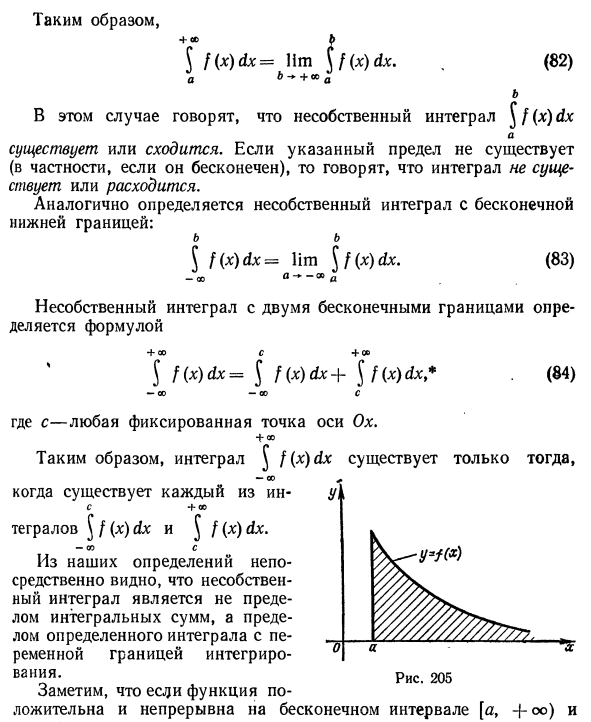
Неправильная интеграция с двумя бесконечными границами определяется по формуле + 00 J f (x) dx = J f (x) dx + \ f (x) dx: с — любая фиксированная точка на оси быка. + со Следовательно, интеграл J f (x) dx существует только в том случае, если -00 ^ соответственный + 00 тегралы [f (x) dx и Jf (x) dx. — и Наше определение прямо указывает на то, что неподходящий интеграл — это не предел интегральной суммы, а предел конкретного интеграла с переменными границами. Ваню. США 205 Эта функция является положительной, непрерывной в течение бесконечного интервала [a, -foo),
| Задачи, приводящие к определенному интегралу | Приближенные методы вычисления определенных интегралов |
| Кривизна плоской кривой | Функции нескольких переменных |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- \ f (x) dx можно интерпретировать как плоский, если он присутствует но Бесконечный изгиб трапеции, окруженный изгибами y-1 (x), бесконечный интервал оси Ox [a, -J-oo) и прямой x * = a (рис. 205). б Это интегрирование разрывной функции и обозначается символом J f (x) dx. но Вот так B s \ f (x) dx => lim [f (x) dx. И с-6-й б В этом случае несоответствующий интеграл J f (x) dx равен но Сосуществовать или сходиться. Если указанный предел не существует, говорят, что интеграл не существует или расходится.
. Подынтегральное выражение разрывно в точке η = 6. и Рассмотрим интеграл \ \ b-xy. Где г <с < но (Для ФΦ1, P dx = I 1 г 1 G 1___I I J (b-xY c-1 ‘a-I l (b-cY ~ * но и JDX = —In (6-x) I = In (b-I) -In (b-c). Если ja <1, то -1 <0, поэтому и Когда µ = 1, lim liin [In (6-a) -In (6-c) j = H-oo. c- * b-0 J ° до X c- * b-0 a Если m> 1, то m — 1> 0, поэтому и
Точно так же, если j (x) является разрывным, когда x приближается к точке a справа, б б \ f (x) dx = lim [f (x) dx, где ea 0, где интеграл сходится но Решения Людмила Фирмаль
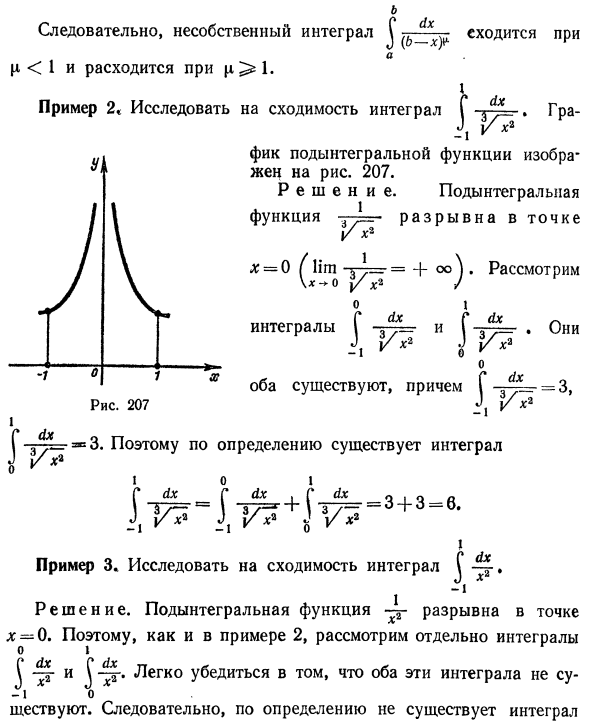
JDX f_hu сходится в но [l <1 и расходящийся Я L jjm Изучите сходимость примера 2, интеграла I. Gra- Коррекция подынтегральной функции показана на рисунке. 207. Решения. интеграл Прерывистый в функции 3 * Для них * = 0 ^ lim + oo j. обзор 0 я интеграл Г и Г • He * 1 В * \ В * о (* Dx Оба существуют, я 3 = 3 Y * 2 s = «3. Следовательно, по определению, В Я Y * J, V * \ V * \ JDX -1 Решения. Подынтегральное выражение разрывно в точке ^ -0. Поэтому рассмотрим интегралы по отдельности, как в примере 2. О себе (И оба эти интеграла -1 о Март. К счастью, по определению, нет никакого интегрального Использовать дх \ — * Если вы действовали формально, 1 JDX Бы получить -1 1 Очевидно, неверный результат \ — £ = — = — 2. Этот результат о х х | -1 -1 Для интеграции положительных функций на сегменты
Использовать дх \ — * Если вы действовали формально, 1 JDX Бы получить -1 1 Очевидно, неверный результат \ — £ = — = — 2. Этот результат о х х | -1 -1 Для интеграции положительных функций на сегменты [–1, 1] не может быть отрицательным. Наша ошибка произошла из-за того, что мы незаконно применили уравнение Ньютона-Лейбница, оцененное в предположении непрерывности подынтегрального выражения над сегментом интегрирования. В нашем случае
Функция имеет бесконечный разрыв в точке x = 0. 3. Признаки несоответствующей интеграции конвергенции В некоторых случаях нет необходимости вычислять неподходящий интеграл, но достаточно знать, сходится ли он или расходится. В таких случаях часто бывает полезно сравнить этот неподходящий интеграл с другим неподходящим интегралом с известной сходимостью или расхождением. Дает теорему, которая устанавливает признак сходимости или расхождения на основе неуместных интеграционных сравнений без доказательств.
Теорема 1. В интервале [a функции f (x) и φ (x) Является непрерывным и удовлетворяет неравенству 0 <φ (x). Далее: но а) Если интеграл ^ f (x) dx сходится, интеграл также сходится но I f (x) dx; но + со б) Если интеграл J f (x) dx расходится, то интеграл J / (x) dx но Это также филиалы. Изучить K интеграл сходимости в Решения. Integrand ^ .——— Сравнить sphunk -m = r. Очевидно, интервал 1 ^ x <- | -oo
^ Vx * chl / * ‘ Но поскольку a = y> 1, ^ -7 сходится (см. Подраздел 1, пример 1). левый \ Однако согласно теореме 1 этот интеграл (* dx. ,] Vx * + \ + 00 Пример 2 « Исследование сходимости интеграла J ln dx Решения. Для интервала 2 1, потому что в x сумма x2 + 1 больше основания натурального логарифма е. Так на этом интервале M * W-1) 1 x ^ T ‘ + CO IDX ■ j расходится (см. Пример 1 в разделе 1). так 2 И этот интеграл также расходится. Теорема 2. Функции f (x) и <p (x) в интервале [a, b) непрерывны, удовлетворяют неравенству 0 <cp (g 🙂 <f (x) и разрыву в точке x = b
Предположим, что есть. Далее: б а) Если интеграл J f (x) dx сходится, интеграл также будет сходиться но В $ <p (x) dx; но В б) интеграл J (p (x) dx расходится, интеграл J / (x) dx Тем не менее, Это также филиалы. 1 Пример 3. Хотите исследовать сходимость одного G 3 A? , __.-. J i / l-x * О В Решения. Подынтегральное выражение непрерывно в интервале [0, 1) и имеет бесконечный разрыв при x = 1. Будете ли вы Сравните функцию с функцией 1 1 час Он непрерывен на отрезке [0, 1) и имеет бесконечный разрыв в точке x — 1. Во-первых, если 0 <Γ; e <1, выполняется неравенство x * ^ x, поэтому неравенство 1-x. Но | / l-1-xi, таким образом, 3 J- <3. так у * у 1 —X Следовательно, подынтегральное выражение 3 1 в интервале [0, 1) в порядке. 1-х *
Меньше, чем функция 1 1 Поскольку интеграл Γ ^ _- сходится (см. Раздел 2, пример 1) Я 1 Теорема также сходится согласно теореме 2. Джей Фур Пример: опрос, где значение K a> 0 сходится + C0 Для dx интеграл является J-p-. б Dx Решения. Рассмотреть возможность интеграции 1 * Для α ^ 1 = б Если а = 1, = = В б. Если a> 1, то a — 1> 0, поэтому lim (6l_e) = lim 0 От B + до b- * + CO ™ б Так что в этом случае, lim lim -j-! — (61_e— 1) = b- + <»v x b + cn 1 a б Если <1, lim | = lim-> = + oo, и + «J x +» 1 ~ a б Dx a = 1 lim \ — = lim lnfr = -foo является общим. b- + + X) для X b + CO 1 + 00 Dx Так что если a> 1, \ сходится, если a <l, L Задыхаясь; + 00 Dx Пример 2. Исследование сходимости интеграла J ТТ ** »4 -00 Решения. Из уравнения (84), которое устанавливает с = 0, + 00 0 + 00 C dx _ G dx. Использовать дх ; l + x®J 1 — \ — x2 t «j tt ^» ‘ и ко-о-о
J, jjj £ -r = Ish lim arctgx | ° = lim (arctgO-arctga) = о-HH- + 00 Точно так же, | х л но И ™ г 14-xg a — «-» прибл. 1 г л a — * — s. 00 1 + х * 2 е так — и То есть интеграл сходится. + 00 б Пример 3, J sin xdx — -cosb Ах ах Существует ограничение b- * + oo, но оно ограничено диапазоном 0-2. Показано, что большинство основных свойств конкретного интеграла сохраняются для сходящегося интеграла с бесконечными пределами. В частности, допустимы выражения подстановки переменных.
Во многих случаях успешное изменение переменной сводит неподходящий интеграл с бесконечными пределами к конкретному интегралу. + 00 Пример 4. Рассчитать интеграл ^^. о Решения. Если x = tan z, L-dz 1 _ 1 4 топор ~ cos2 г * (1 -M2) a ~ (сек2 г) ~ C0S Кроме того, если r изменяется от 0, x изменяется от 0 до -f 00. Таким образом, L l f ^ -f ^ -j1 *? ** — * — + «J
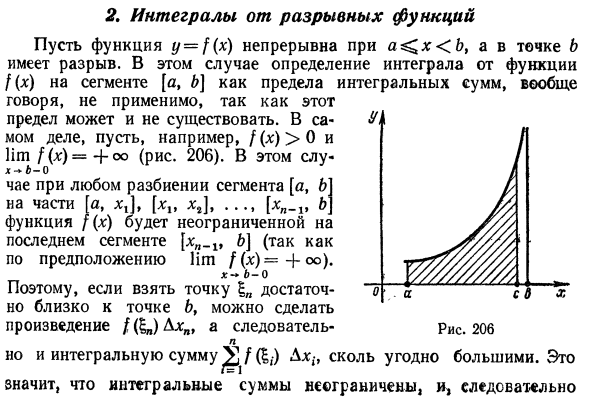
Интегрирование разрывных функций Предположим, что функция y = f (x) непрерывна для a ^ x 0 и lim f (x) = + oo (рис. 206). В этом случае Кроме того, для разбиения на сегменты [i, b parts [a, *,], [xlf xt], …, [xn.lt b ] функция j (x) является последним сегментом [x „ _lt b] (потому что по предположению lim f (x) -f оо). х-б-0 Следовательно, если точка xn достаточно близка к точке 6, произведение f (tn) A: n может быть создано, N Интегральная сумма / / (6, -) может быть произвольно увеличена. Это означает, что сумма интегралов не ограничена, и поэтому Рис. 206
Нет никаких ограничений на обнуление шага раздела. В этом случае, однако, понятие интеграции может быть обобщено, несмотря на то, что предыдущее определение интеграции не является приемлемым. Прежде чем приступить к определению Пример. Рассмотрим функцию y = — {=. Цель этой функции 1 * Бесконечность как х -1 слева. Следовательно, сегмент [0, 1] не может составлять целую сумму. Однако на отрезке [0, c] (0 2. с 1-0
Это ограничение называется прерывистой неправильной интеграцией Я -В функциональном сегменте [0, 1]. И Дж * Вот так Hnn-> r = lim 2 (l-V до c) = 2. J V \ —X C-1-O ^ j —X C-1 -0 ‘ Чтобы подвести итог этого примера, рассмотрим функцию y = f (x). Это прерывисто в точке b отрезка [a, b] и непрерывно в отрезке [a, c]. с — произвольная точка в интервале (а, б) (см. рис. 206)) и определенный интеграл J f (x) dx, когда c— + b слева но До окончательного предела, предел eptet называется неуместным
