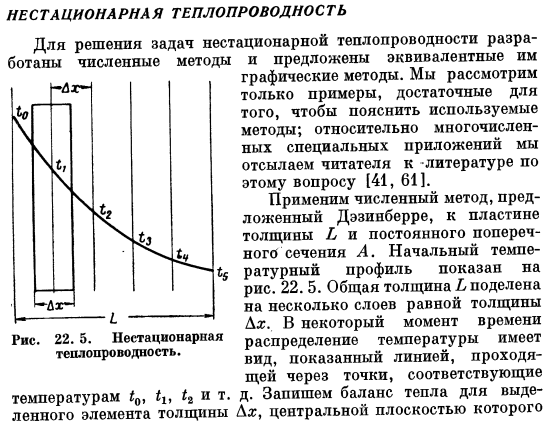


- Для решения задачи нестационарной теплопроводности, методы и соответствующие им предложения. Графический способ. Рассмотрим только те примеры, которые достаточны для объяснения методов для получения большого количества специальных приложений обратитесь к читателю с литературой по этому вопросу. Примените численный метод, предложенный Desipberra, к пластинам толщины b и некоторого поперечного сечения A. начальный температурный профиль показан на рисунке 5. 22. 5. Общая толщина b делится на несколько слоев одинаковой толщины J.
В некоторой точке распределение температуры показано линией, проходящей через соответствующую точку, например, температура * 0. Толщина LX элемента, центральная грань которого является плоскостью 2.Возьмите температурный градиент слева от элемента, в виде—1, °L * температурный градиент справа «Так, чтобы тепловой поток наружу был ка Скорость накопления энергии выбранного элемента, представленная конечной разностью, равна a & x $Ср -, где — Повышение температуры элементов в ДТ. Из этих 3 терминов можно создать формулу энергосбережения ка(Р0 ^ / х)_ ка(*!- ») Я ДХ ДХ ДХ ’ Свари его. X Dt ЛРН *(ЛК) » (22.14) Кроме того, J и Dt могут быть выбраны произвольно.
Обычно пространственные приращения выбираются таким образом, чтобы число приращений было целым числом. В случае ДТ сохраняется свобода выбора. Если сумма^ d ^обозначается символом M, то формула(22. Четырнадцать) Я вижу это. * о + * 1(ЛГ-2) — Н2 1 ———- л ——- (22.15)) Инкрементный Dm определяется выбором модуля M. Если M выбрано равным 2, то формула(22. 15) — это 1 [=. В этом деле、 СД =Ве.»АА:) 2 (22.16) Если требуется более высокая точность, выбирается большое значение модуля M, но выбор M = 2 имеет то преимущество, что вычисление сводится к получению среднего арифметического. Графическое решение задачи, в которой используется M = 2, известно как метод Шмидта.
Составляется график начального распределения температуры, и на переменном этапе расчета соединяются точки, разделенные двумя базовыми слоями. Пример 22 показывает, как вычислять как графическими, так и численными методами. Пример 22.3 Используя Луч, уже описанный в Примере 21, мы покажем вам, как делать графики и числа.2.Резиновый лист толщиной 12,7 мм первоначально был 22°C, но нагревается с обеих сторон из-за повышения температуры до и после . Тема поддерживается этим значением.
- Температуропроводность. Предполагается, что листы разделены на 2 слоя толщиной 12 мм соответственно, и если выбрано M = 2, то приращение времени равно Lm — * eCp = * 2L2’1 ^ 211 = 0.00858 h = 0> 515 минут 2 X 2-2, 6-S. Если решение принимается до тех пор, пока LlRp $не будет известно, сколько времени потребуется для достижения 143,3°C в средней линии, число будет 18,7 / 0,515 = 36,3 (как показано в Примере). 21.2, равный 18 7 минутам).Потому что это так много шагов, вы не можете привести решение до тех пор. Однако из того же примера видно, что средняя температура через 5 минут (9,7 шага) составляет 102,8 с. Это и есть цель. После этого производится проверка этого значения.
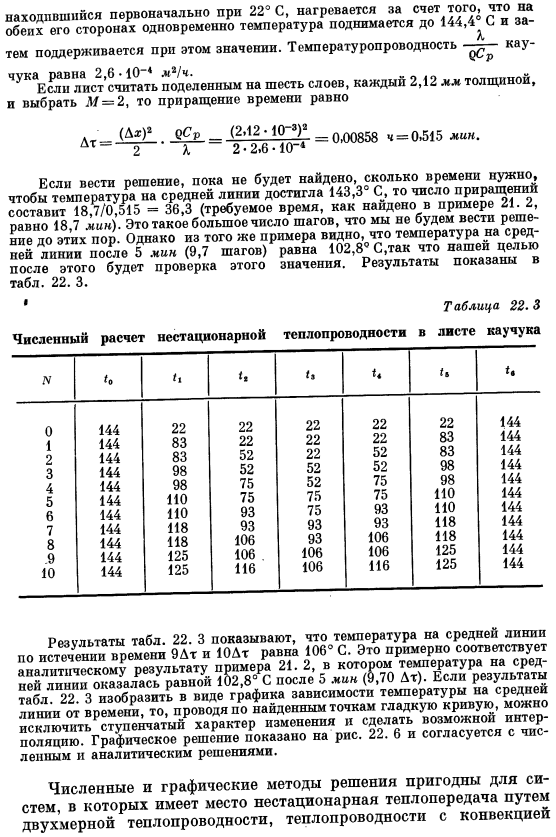
Результаты приведены в таблице. 22.3. Таблица 22. 3. Численный расчет нестационарной теплопроводности резинового листа N * 0 1 0 1 2 3 4 5 6 7 8.9 10 144 144 144 144 144 144 144 144 144 144 144 144 144 83 83 83 83 98 98 110 110 118 118 125 125 22 22 52 52 75 75 93 93 106 106 116 22 22 22 52 52 75 75 93 93 106 106 22 22 52 52 75 75 93 93 106 106 116 22 22 83 83 98 98 110 110 118 118 125 125 144 144 144 144 144 144 144 144 144 144 144 144 Вкладка Трансальп рублей’ltats. 22. 3 указывает, что средняя температура линии после часов 9Dt и UDt составляет 106°C. Это пример 21. Почти соответствует результатам анализа 2.
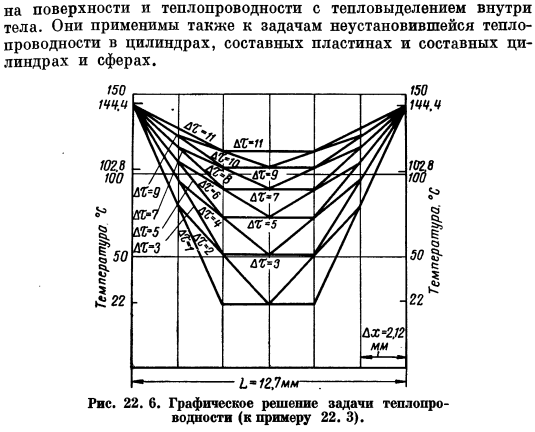
Если результаты, приведенные в таблице 22 3, построены в зависимости от температуры и времени ниши, то по найденным точкам можно построить плавную кривую, исключающую поэтапный характер изменений и позволяющую проводить полис. Графические решения проиллюстрированы на рисунке. 22. 6 и лен и согласился с решением анализа.
Численное и графическое решение подходит для систем С 2-мерной теплопроводностью, теплопроводностью с конвекцией на поверхности и нестационарной теплопередачей с тепловыделением на поверхности. body. It смогите также быть приложено к переходным проблемам термальной проводимости цилиндров, составных плит, составных цилиндров, и сфер. Рисунок 22.
Смотрите также:
| Численные, графические и аналоговые методы в исследовании теплопроводности | Аналоговые методы |
| Стационарная теплопроводность | Конвективная теплоотдача при поперечном обтекании цилиндра |
