Оглавление:







Нестационарный теплообмен в твердых телах
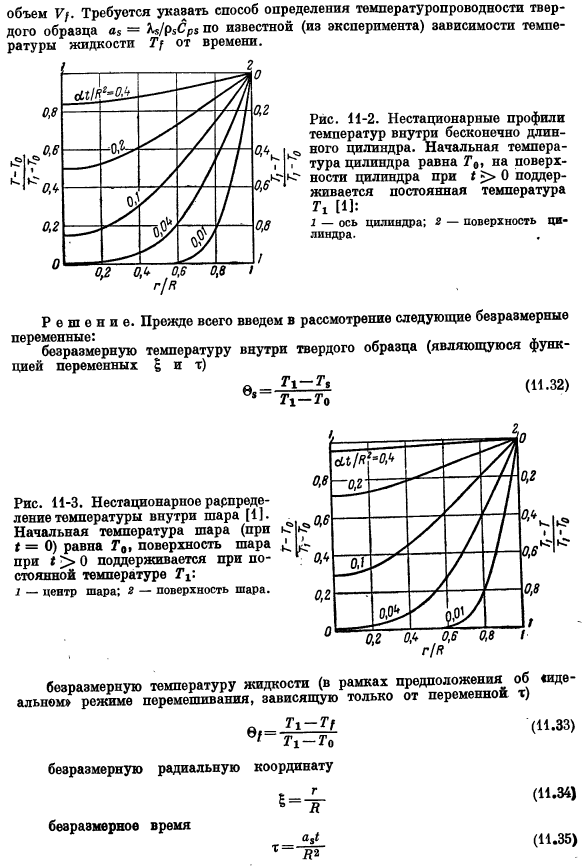
- Для теплопередачи в твердых телах уравнение сохранения энергии (10.19), в котором подставляется закон теплопроводности Фурье, имеет вид (в-Зир> (11.1). Если теплопроводность не зависит от температуры, но одинакова во всех точках пространства, то формулу (11.1) можно описать в более простой форме. Здесь значение A = MPr называется коэффициентом теплопроводности твердого тела. Уравнение (11.2) является одним из 1 наиболее изученных уравнений в теоретической физике. Знаменитая книга Карслоу и Ягера [1] целиком посвящена изложению путей разрешения этой связи.
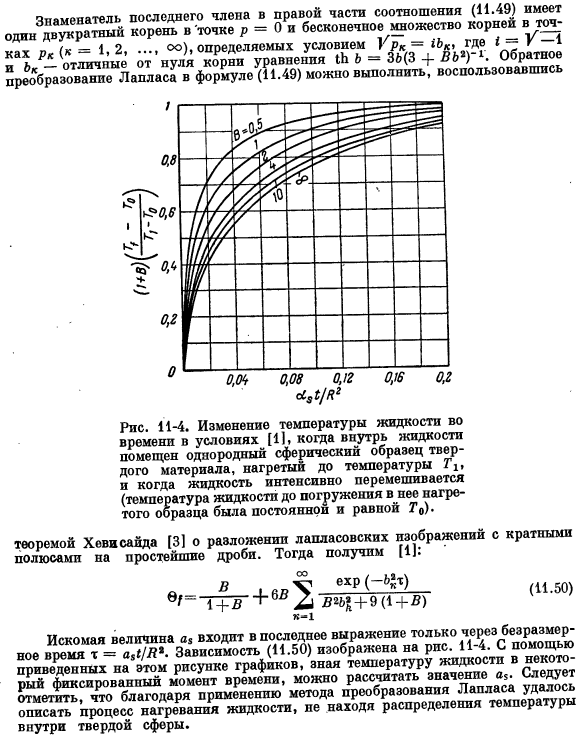
Книга должна быть хорошо известна всем инженерам и ученым, работающим в области прикладной физики, но в ней дается табличное решение для самых разнообразных начальных и граничных условий. Среди них есть выражение распределения температур многих систем, которое часто встречается на практике. В этом разделе описаны 2 простейшие задачи нестационарного теплообмена. Целью данного исследования является ознакомление читателя с различными задачами, связанными с расчетом переходного режима теплообмена. Полученные ниже 2 простейших решения уравнения (11.2) (примеры 11-1 и 11-2) основаны на использовании метода самоподобия переменных и метода разделения переменных.
Для вычисления Локальных коэффициентов восстановления использовалось уравнение (10-13), в которое подставлялись измеренные температуры поверхности, скорость и статическая температура потока. Людмила Фирмаль
Эти методы уже используются при анализе аналогичных гидродинамических задач (см. раздел 4.1).Пример 11-3 предназначен для иллюстрации очень эффективного метода преобразования Лапласа для решения многих задач. Нестационарные задачи. Читатели, которые хотят знать более сложные вопросы теплопередачи, могут легко найти их в книге выше[1]. Пример 11-1.Нагрев полумассы материала коттеджа, которая занимает легкое место, был температурой Т». при y = 0 это было похоже на прыжок по заданной поверхности. Решение.
В Безразмерная температура Формат размер Уже перед аргументами» Из формул (11.8) и (11.9), V>⁶t-температура T отличается от начальной температуры-менее чем на 1% от разности T₀ 差 (TJ-если требуется найти распределение температуры слоя с конечной толщиной, то 6 g мало по сравнению с толщиной слоя、 * Аналогичные проблемы в случае [2]. Таким образом, глубина проникновения теплового фронта изменяется во времени пропорционально t ’1′, а поверхностный тепловой поток y = 0 равен Пример 11-2 нагревательная плита.
- Сплошной слой Безразмерная температура Материал, занимающий поверхность y = + btem-Etegaer3a^ ryIG», T (11.11). Безразмерное время (11.12) (11.13) Такой выбор безразмерных переменных позволяет очень легко представить исходные дифференциальные уравнения и соответствующие им граничные условия ДВ дге ДТ 2 6 = 1 при m = 0 H =1, Если±6 = 0 (11.14) (11.15)) (11.16) (11.17) Присвоить продукту равенство (11.17) fg. As итог 1 dg_1 Да / Г Д-Р Ф Ди)3 согласно опрелю, левая часть последнего уравнения зависит только от m, а правая-от условий. (11.18) (11.24) АУ = 4pSlekhr (11.26) Где Dₙ= БТР» + а — ₍»>с.
Коэффициент Dₙ можно определить из начального условия (11.15).Согласно этому условию, отношения Умножьте часть соотношения (11.27) на cos (((m+*/))], а затем интегрируйте его из q = −1 в noover/) в диапазоне q = +1. (11.28)) Расчет показывает, что в правой части уравнения (11.28) имеется 1 член: m = n.
Цилиндр был сделан из резины, для того чтобы ликвидировать температурное выравнивание путем теплопроводности в твердом материале. Людмила Фирмаль
B для вычисления коэффициента Dₘ’- Она будет равна нулю, за исключением того, что результатом будет следующая формула: 4〜(m + 4〜)^ +43ⁱⁿ [(W T) 2LP] г (т т) i l Если мы знаем коэффициент Dₘ, мы можем переписать решение (11.26) в следующем окончательном виде. *- Г ^ Г Безразмерное время (11.34)) (11.35 утра)) (11.32)-(11.35) вышеуказанная задача формулируется следующим образом Твердый раствор образца а. я(11.36)56; 3/50、\(11.40) l » F’srl6-aFJ 5t W-55 D_1 для M = 0 0,= 0(11.37) для M = 0 0 / = 1(Н-41) Если J = i es = 0. (11.38) Если 5 = 0 0, тоCps-безразмерная величина. В / Я Против — Твердая фаза и твердая фаза. Давайте воссоздадим его.
Все (11.36) и условия гранита (11.40)(11.37)、(11.38)、(11.39) Преобразование Лапласа*: да; Твердый образец— (11.42)-、3/50、\(11.45) — ’»(АР)、-、 5 = 1, Если 0J = 0 /(11.43) Если 5 (11.44) Общая форма решения уравнения (11.42) имеет вид с,= г-ш(/ 75)+ — й-ч (/ПБ) (11.46) Согласно граничному условию (11.44), постоянная D должна быть равна нулю. Объедините выражение (11.46) и выражение (11.45), чтобы получить: е / = с — J — + — ^ — (ш / Ф-РПЧ / Ф) (11.47) Константу С можно вычислить, подставив формулы (11.46) и (11.47) в граничные условия (11.43).
Смотрите также:
