Объем тела вращения
Пусть функция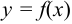 
непрерывна и дифференцируема на 
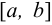и пусть в системе координат на плоскости дан график этой функции, по которому соответствует криволинейная трапеция 
.
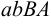Телом вращения будем называть тело, которое образуется при вращении этой криволинейной трапеции вокруг оси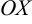 
.
Разобьем отрезок 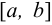точками деления 
, 
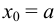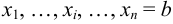на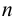 
частей. Если через эти точки провести плоскости, перпендикулярные оси 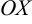, то тело вращения разобьется на 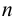малых тел вращения.
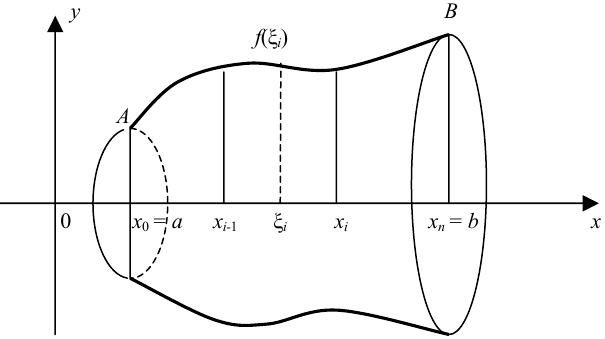
Возьмем точку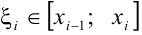 
и построим цилиндр радиуса 
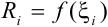с высотой 
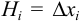. Тогда объем малого тела вращения 
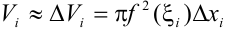. В качестве объема тела вращения естественно считать предел суммы всех элементарных объемов 
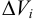, которые заменяют объемы малых тел вращения 
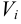по всем точкам деления при условии, что 
:
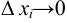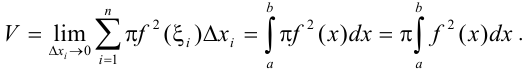
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
