Оглавление:
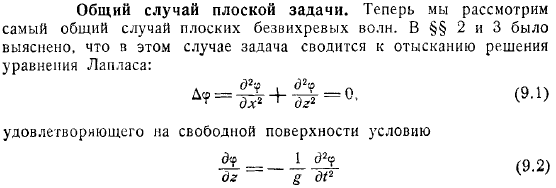

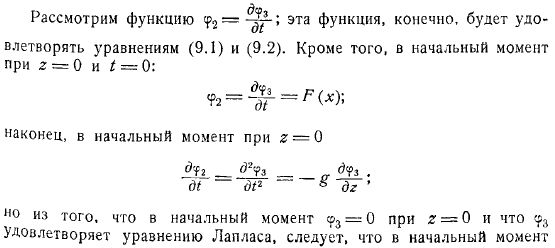



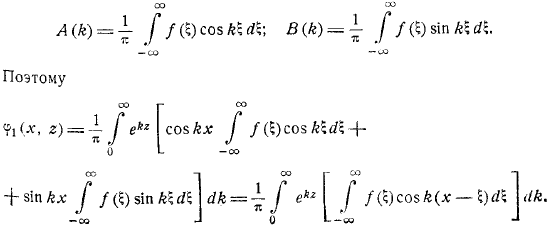
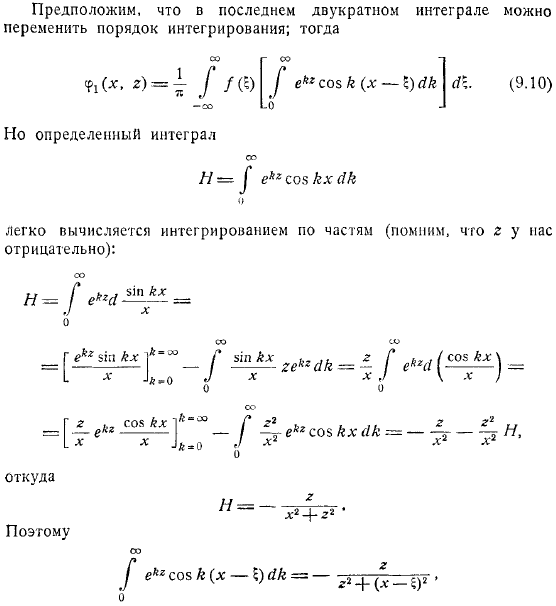


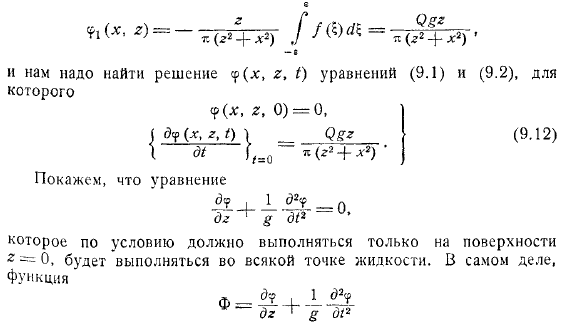

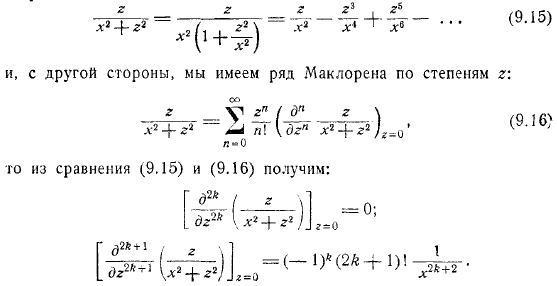
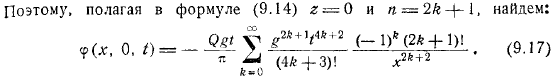

Общий случай плоской задачи
Теперь рассмотрим наиболее распространенный случай невращающейся плоскости. Оказывается, в этом случае задача сводится к нахождению решения уравнения Лапласа. Соблюдайте условия гидромеханики на свободной поверхности и начальные условия.
Кроме того, они имеют следующие физические значения:если существует уравнение для свободной поверхности. Запускает начальное распределение скорости. Из-за линейности уравнения сумма решений этих уравнений также является решением.
- Найти функцию групповой скорости и начальное условие. В этом случае достаточно ограничиться. Факт, выяснить можно. Найти решение системы уравнений, удовлетворяющее начальным условиям.
- Конечно, принимая во внимание функцию этой функции, мы заполняем. Кроме того, в первый момент.
Наконец, учитывая, что в первый момент, в первый момент его, удовлетворяют уравнению Лапласа, следует в первый момент равный нулю. Людмила Фирмаль
Поэтому в первый момент, и поэтому. Поэтому функция является необходимым решением. Итак, находим решение уравнения по начальным условиям.
Указывает начальное значение и тогда, согласно вышесказанному, первыми причинами состояния являются. А теперь выясни. Очевидно удовлетворен Уравнение Лапласа. Однако мы неоднократно использовали следующие решения уравнения Лапласа. Где были какие-то константы.
- Вы можете переписать этот интеграл в другую форму, вычисляя Косинус разности и вводя нотацию. Вот, какая-то константа. Линейности уравнения Лапласа позволяет сформировать более общее решение уравнения Лапласа.
- Для того чтобы сформировать наиболее распространенное решение уравнения Лапласа, необходимо принять всевозможные дополнительные величины.
Это совершенно необязательно. Но тогда сумма становится профиль волны неким интегралом. Сумма может рассматриваться как приближение этого. To показать, что найденное решение является наиболее распространенным, нам нужно доказать, что мы можем выбрать такую функцию после подстановки граничного условия в функцию, которая удовлетворяет его.
Следовательно, определяющий интеграл Людмила Фирмаль
To решите это уравнение, используя интегральное выражение Фурье, которое справедливо при определенных условиях вы можете переписать его так. Если вы сравните последнее выражение, вы увидите, что его нужно принять в последних подынтегральных выражениях мы предполагаем, что порядок интегралов может быть изменен.
Тем не менее, определенные интегралы легко вычисляется интегрированием по частям (помните, что путь отрицательный. Так где же? Эта формула определяет решение уравнения Лапласа для области, которая будет являться конкретной функцией .
Далее обратимся к решению гидродинамической задачи. Рассмотрим частный случай следующих начальных условий: за исключением небольшого участка оси, охватывающего начало координат, сделайте его равным нулю везде, а в этом участке (пусть он имеет координату в конце). И предположим, что функция очень большая, а интеграл хранит конечное значение.
Найдите значение количества. Из уравнения мы получаем следующую физическую интерпретацию условия: в первый момент поверхность жидкости везде горизонтальна, за исключением области вблизи оси, и здесь в первый момент возникает сильно приподнятая поверхность жидкости, а объем приподнятой жидкости становится равным (плоскость, единица движения, если толщина жидкости перпендикулярна направлению оси). Необходимо определить дальнейшее движение жидкости.
Число считается равным. Функция будет бесконечно большой. Конечно, это физически невозможно. Тем не менее, расчет значительно. Необходимо тщательно применять формулу при интерпретации полученных результатов, имея в виду те упрощения, которые были сделаны.
При допущениях выражение принимает вид. И тогда вам нужно найти решение уравнения. Уравнение в зависимости от условий, поверхность должна быть заполнена только и в любой точке. Факт, функция конечно, это решение уравнения Лапласа .
С другой стороны, если функция равна нулю, следовательно, функция равна. Здесь вы найдете расширенные функции в ряд Маклорена власти. Но мы легко можем сделать вывод, используя формулу, это выглядит так: следовательно, искомое решение.
Узнайте, что изменится. И, с другой стороны, у нас есть ряд полномочий маклорина. Тогда вы получите от сравнения. Итак, предполагая по формуле, это выглядит так.
