Оглавление:










Окрестности в метрическом пространстве
- Концепция соседа в любой метрике Пространство является обобщением аналогичной концепции Точка числовой линии. е положительное число Число (e> 0) и a является некоторой метрической точкой (A∈M) пространства M). Определение 5.2. многие U (a, e) = {x e M: p (a, x) 0), Называется замкнутой сферой с радиусом r с центром в <* • Наконец, точка на расстоянии r от точки a, Сформируйте сферу с радиусом r в центре как p (a, a 🙂 = r О баллах. Итак, электронная окрестность в метрическом пространстве Вокруг этой точки есть открытый шар с радиусом е. в В частности, e-окрестность εR для метрики вида (5.2) и (5.3) находятся в числовой строке Интервал по центру с длиной 2е. на плоскости электронного соседства
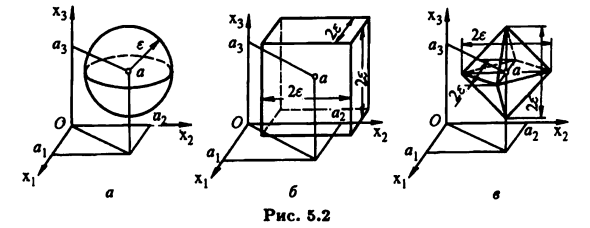
Точка a∈R2 для метрики (5.2) является окружностью (открытой, Центр радиуса е) В этот момент (рисунок 5.1, а) и случай (5.3) -квадрат (нет В трех измерениях Космическая метрика соседа a 6 R3 метрика (5.2) шар (Без граничной сферы) с радиусом е в этой точке (Рис. 5.2, а) и метрика (5.3) соответственно кубы с ребрами 2e (рисунок 5.2.6) и октаэдра с диагональю 2e (рисунок 5.2, c), таким образом Термин «открытый шар» не нужно понимать буквально. Теперь U (a, £ 1) и U (a, £ 2) являются одной электронной окрестностью Та же точка а в метрическом пространстве Число должно быть {{i}, £ 2} = минимум £ 1 U (a, £ i) может быть включено в U (a, € 2) U (a, £ 1) flU (a, £ 2) = U (a, £ 1) = U (a, min {£ b £ 2}), (5.4)
Границы профиля) соответственно боковой (рис. 5.1.6) и Диагональ (рисунок 5.1, в) равна 2е. Людмила Фирмаль
Т.е. любые два пересечения — это одно и то же соседство Дело в том, что около £ для этой точки. Теорема 5.1 (Свойство отделимости). Любые два Разные точки метрики х б Пространство настоящего соседа \ J (x, e) и U (y, £) Пустое пересечение. 4 Согласно определению 5.1 аксиома а) Если χφ /> (x, y)> 0, положим f ° (x, y) = 3 £. тогда U (i, e) U U (y, e) = 0. На самом деле это пересечение Содержит несколько точек r и из аксиомы c) Для определений 5.1 и 5.2 электронной окрестности: = p (x, y) <p (x, z) + p (z, y) <£ + £ = 2 £, Это невозможно ► Особенностью отделимости, принятой в качестве аксиомы, является Класс пространства под названием Хаусдорф по имени Немецкий математик Ф. Хаусдорф (1868-1942).
Определение 5.3. Набор U C M называется Открыто, если включено с каждой точкой Некоторые £ — соседи этого пункта. Термины «открытый разрыв» и «открытый мяч» уже Используется раньше. Докажите, что это было оправдано Следующая теорема. Теорема 5.2. Раскрытый шар U = {x € M: p (a, x) <r} Радиуса r с центром в точке a метрического пространства M Есть открытая толпа. <Xo e U и p (a, xo) = r0 <r. Непрерывность U («o» £) для точки x0 с радиусом e <r-й. Это э-ок Согласно определению 5.2 U. На самом деле, любой x∈U (xo, e) из-за неравенства треугольник p (a, x) <p (a, xo) + p (xo, x) <rQ + e < Поэтому откройте шар и одну из его точек ho также включает электронную окрестность этой точки. Соответствует определению открытого множества.
- ► Определение 5.4. Любой открытый набор Весовое пространство M, содержащее точку x0, называется Вблизи этой точки обычно указывается U (xo). Произвольная g-окрестность точки U (x0, e) согласно теореме 5.2 ho — открытый набор, включающий эту точку, Так что около х0. Конечно же Согласно открытому определению 5.3, окрестность U (zo) точки x0 Часть набора включает это ^ -соседство U (xo, e) Точка. Из-за этой взаимосвязи все заявления Этого достаточно для окрестности точек в метрическом пространстве Сформулируйте и докажите только электронную окрестность
Суть проблемы. Теорема 5.3. Серия открытых комбинаций Конечные множества множеств и пересечения Открытый набор — это открытый набор. L открытое множество Открыто, продолжается непосредственно из определения 5.3 Set. Сделать точку xq принадлежащей открытой Установите Ui, 1b, …, Un, включенные в начале из них U смежный U (xq, £ i), 2nd-U смежный
Настаивайте на том, что объединение является добровольным множество окрестностей х0 и пересечение Конечное число окрестностей этой точки является окрестностью x0, Следующая теорема позволяет. Людмила Фирмаль
Далее это точка Шжо-е-окрестности, £), такая как U (т.е. £ 2) Где e = min {ei, € 2, — .., £ n} входит в каждый набор Ubib, …, Un и, следовательно, Пересечения. Следовательно, пересечение конечной населенности Открытый набор с любой точкой xq содержит Некоторые ^ -соседи этой точки соответствуют Определение открытого множества 5.3. ► Определение 5.5. Различные показатели ASA Расстояние от Любая точка xq € M для каждой точки в этом наборе Некоторая константа C> 0, т.е. если 3C> 0: Vs0 6 M Va £ A p (x0, a) ^ C. (5.5) Если (5.5) выполнено, Любые две точки из A a \ и a 1, fl2)
1, n0) + p (a2, x0) > 0 в A имеет пару точек ai, a2, p (a \ y a2)> > C. В этом случае и любая фиксированная точка хо € М Если C> 0, вы можете найти точку A. p (a? 0, a)> C. Для ограниченного множества A рассмотрим количество diamA = sup p (a \, a2), Это называется диаметром набора. Следовательно, все точки ограниченного множества AC M Содержится в шаре конечного радиуса в центре Точка xq метрического пространства M. Таким образом, Разработать определение, эквивалентное определению
5.5. Определение 5.6. Многие AC M называются Ограничено, если все очки включены в мяч Конечный радиус (или множество A входит в такое) Болл). Числовая линия задает точку A C R Формальное определение границы эквивалентно Определение упорядоченных подмножеств 2.5 Set. Определения 5.5 и 5.6 Множество A C R содержится в конечном отрезке Номерная строка.
Смотрите также:
| Группа подстановок | Характерные точки множеств |
| Понятие метрического пространства | Замкнутые множества |
