Оглавление:





Основной постулат метрологии
- Процедура, которая сравнивает неизвестный размер с известным размером. Первое-второе выражение множественного или дробного отношения математически записывается как о ( 2) = x (2). Здесь соответствующая единица СИ функционирует как известный размер 2 при измерении физических величин. Информацию об этом можно найти либо в измерениях материала, либо в маркировке на считывателе, либо в калибровочных характеристиках прибора. При измерении сенсорных стимулов используется концепция единиц СИ, хранящихся в человеческой памяти, и измеренное значение измеряется с учетом (2).
При взвешивании сравнения иногда Создано с использованием стандартов, базовых или высококачественных идей: Кроме того, по сравнению с другими значениями значения являются физическими и нефизическими. В последнем случае эти значения выражаются, например, в точках. Уравнение (2), как и уравнение (3), называется уравнением измерения. И еще одно действие представляет собой процедуру сравнения, некоторые действия, которые на самом деле являются измеренными значениями. Основная особенность этой процедуры заключается в том, что при многократном измерении одного и того же значения определенного размера результат сравнения x, называемый критерием шкалы отношения, всегда отличается.
В некоторых случаях деление на равные части допуска, представленного линейной величиной, заменяется делением на части, где граница представлена О. Людмила Фирмаль
Этот, казалось бы, парадоксальный феномен отличает реальную деятельность от теоретических моделей. о Из уравнения (1). Огромный опыт фактических измерений, накопленный к настоящему времени, еще больше указывает на то, что в натуральных числах они совершенно разные. Теоретически, отношение двух размеров у должно быть четко определенным неслучайным числом. Фактически, сравнение этих размеров является результатом многих случайных и неслучайных ситуаций.
Это сделано ниже, но его точный расчет невозможен, поэтому результаты сравнения отличаются друг от друга, эта позиция, установленная практикой, сформулирована в форме аксиомы, Это можно назвать предпосылкой: эталоном является случайное число, поэтому значение измеренной величины существует, но не может быть определено. Первая часть этого утверждения является отражением материалистической концепции материаловедения, а вторая часть основана на решении, которое выявляет противоречие и обеспечивает основу для прогресса в области измерения. Из основной идеи измерения вы также можете видеть, что результат сравнения х неоднозначен.
Для обеспечения единообразия, сопоставимости, надежности, точности и объективности измерений в таких условиях принимаются дополнительные правовые меры и меры по измерению, связанные с получением, представлением и использованием результатов измерений. Все аспекты должны быть строго регламентированы. Это в некоторой степени объясняет существование законодательной метрологии, государственного надзора и ведомственного управления в отношении метрологических правил, требований и норм, соответствия государственным и ведомственным метрологическим службам.
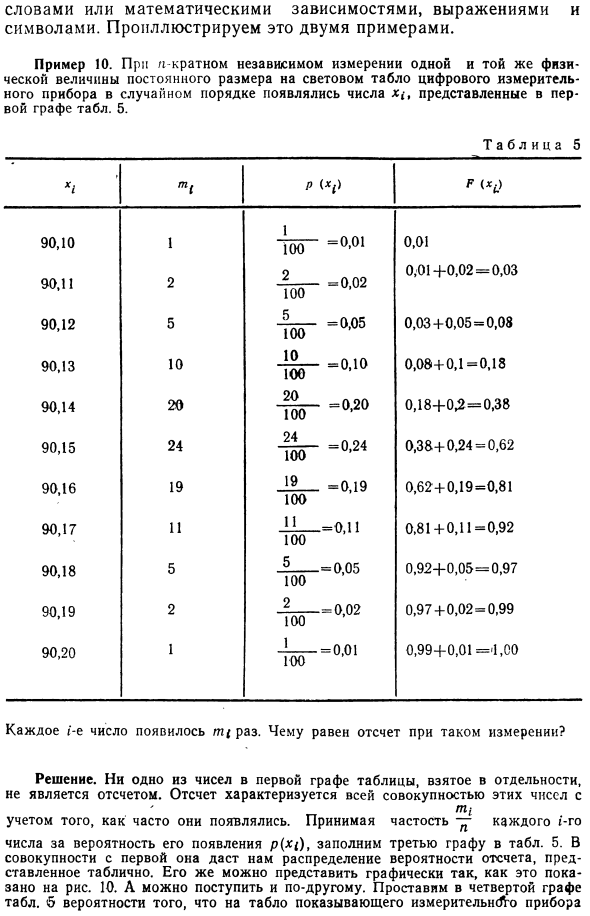
Многие трудности в измерении связаны с тем, что счет не может быть представлен одним числом. Могу только объяснить Слово или математическая зависимость, выражение, символ. Два примера иллюстрируют это. Пример 10. 11-е значение стоящего устройства находится в случайном столбце 1 таблицы. 5. На световой панели заказа цифрового счетчика отображалось числовое значение xb, где сначала отображаются несколько независимых измерений одинакового размера.
Таблица 5. 90.10 90.11 90.12 90.13 90.14 90.15 90.16 90.17 90.18 90.19 90.20 2 5 10 20 24 19 5 2 1 Loo 5 °> 01 T G — — = 0,05 100 * 9 -0,19 100 L- = o, 11 100 L = 0,05 100 два. — 0,02 100 -1 ^ — = 0,01 0,01 0,01 + 0,02 = 0,03 0,03 + 0,05 = 0,08 0,08 + 0,1 = 0,18 0,18 + 0,2 = 0,38 0,38 + 0,24 = 0,62 0,62 + 0,19 = 0,81 0,81 + 0,11 = 0,92 0,92 + 0,05 = 0, 97 0,97 + 0,02 = 0,99 0,99 + 0,01 = 4,00 Решения. Числа в первом столбце таблицы не взяты по отдельности, но не являются обратным отсчетом. Обратный отсчет характеризуется суммой этих чисел с учетом количества вхождений. Введите каждую частоту (i-е число как ее вероятность появления p (X ()) в третьем столбце таблицы 5.
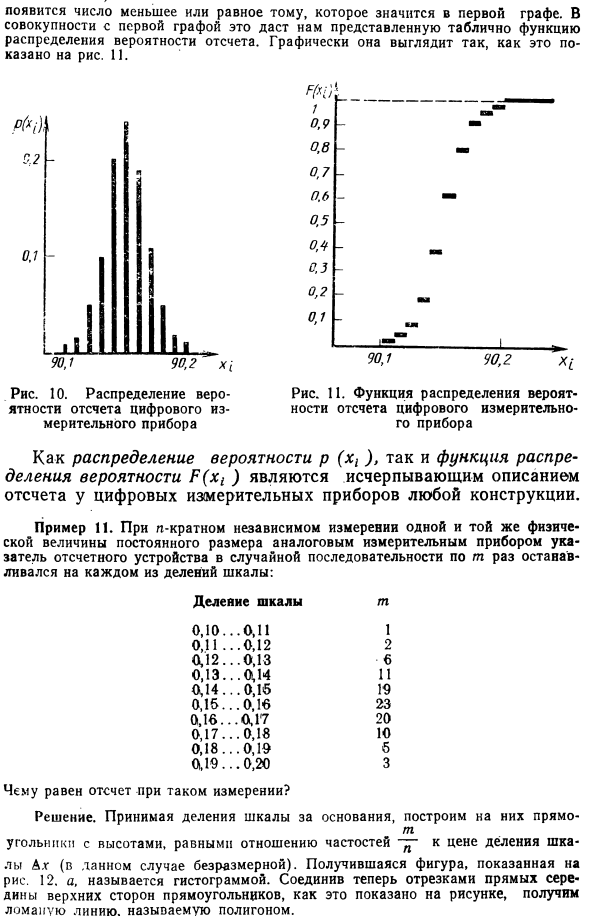
Вместе с первым столбцом распределение вероятности считывания, отображаемое в таблице, составляет Однако можно действовать по-другому: в четвертом столбце таблицы 5 введите вероятность того, что инструмент появится на дисплее. Отображение первого числа следующих номера в сочетании с колонкой, которая по распределению опорного кадра получается. подсчитывать Появляется в первом столбце. в Измерительный инструмент метр Распределение вероятности p (x1) и функция распределения вероятности P (x1) являются исчерпывающим описанием ссылок на цифровые конструкции для всех конструкций. Пример 11.
Когда аналоговое измерительное устройство выполняло независимое измерение одной и той же физической величины постоянного размера, указатель считывающего устройства произвольно останавливался m раз в каждом сегменте тика. градация 0,10 … 0,11 1 Ох и … 0,12 2 D12 … O.13 6 0,13 … 0,14 11 0,14 … 0,15 10 0,15 … 0,16 23 0,16 … 0,17 20 0,17 … 0,18 10 0,18 … 0,19 б 0,19 … 0,20 3 Какой отсчет для этого измерения Решения.
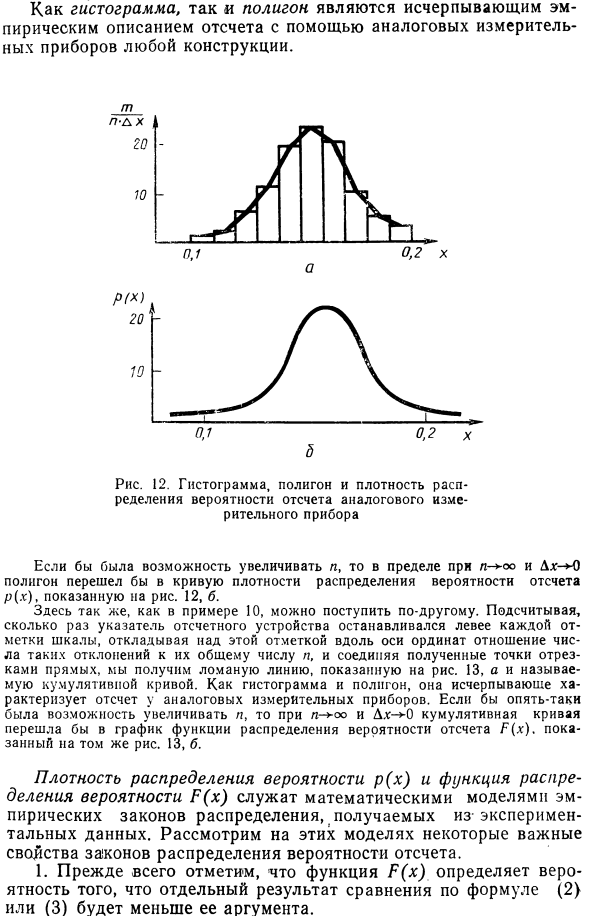
Взятие Квадратный масштаб деления топоров с высотой, равной соотношению частот (в данном случае безразмерно). Полученная диаграмма показана на рисунке. 12. а, называется гистограммой. Как показано на рисунке, когда прямая линия соединена в центре верхней стороны прямоугольника, получается ломаная линия, называемая многоугольником. И гистограммы, и полигоны являются исчерпывающими эмпирическими описаниями показаний с использованием произвольно разработанных аналоговых инструментов.
Рисунок 12. Гистограмма, полигон и плотность, определяющие вероятность чтения аналогового ритуального устройства Если л можно увеличить, в пределах у0 и Dx-М, многоугольники достигнет кривой распределения плотности вероятности опорной вероятности р (х), показанного на 12, б. Пример 10, один тип. подсчитывать Слева от каждой осени на этой ординате Общее количество точек отсечения Линия, пунктирная линия 13 на рисунке, телефон Эмулирует кривую. Комплексная характеристика показаний аналоговых приборов, таких как гистограммы и полигоны.
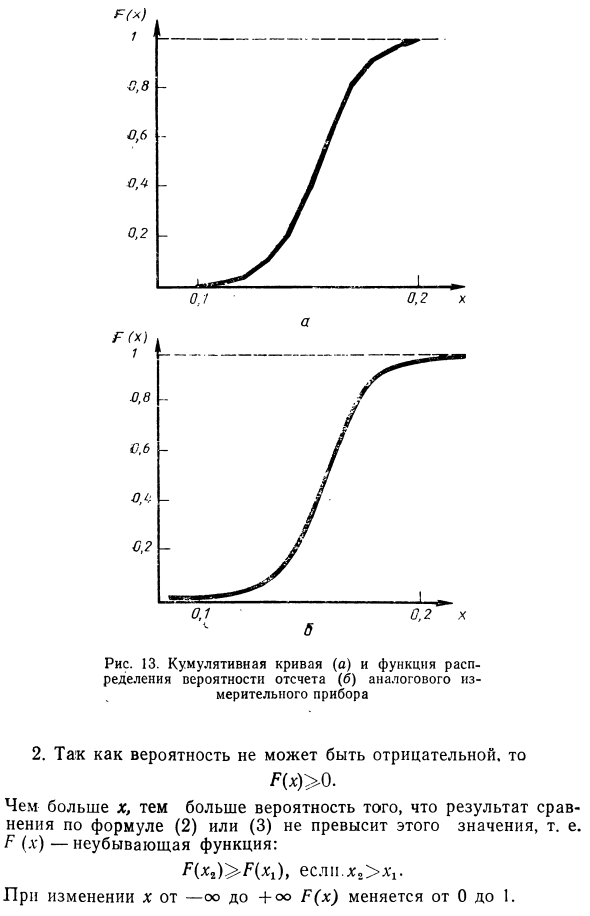
Опять же, если может быть увеличено, для — * x> и Dx — — 0 кумулятивная кривая является графиком функции распределения вероятностей, которая читает (x). Показано на той же фотографии. 13 б Плотность вероятности p (x) и функция распределения вероятности P (x) функционируют как математическая модель эмпирических правил распределения, полученных из экспериментальных данных. Для этих моделей рассмотрим некоторые важные характеристики закона распределения эталонных вероятностей. 1. Во-первых, обратите внимание, что функция P (x) определяет вероятность того, что результат отдельного сравнения из уравнения (2 или (3) будет меньше, чем его аргумент. 2.
- Вероятность никогда не будет отрицательной, / (X)> 0. Чем больше х, тем больше вероятность того, что результат сравнения с использованием уравнения (2) или (3) не будет превышать это значение. То есть G (x) является неубывающей функцией. h (x1)> T (x1), истинно x1> X1. Когда x изменяется от -oo до + oo, P (x) изменяется от 0 до 1. 3. Результат индивидуального сравнения формулы (2) или (3 / вероятность P (x \) меньше, чем X1 и вероятность P (xg) меньше, чем X1. Следовательно, формула (2) или (3) Интервал xy x2 равен разности значений P (x). P (x1 x x,) — (X.) — (x1). Аналоговое измерительное устройство X И x2 может быть произвольно выбрано между собой. X is- * XrP (xr) -P (x \) 0.
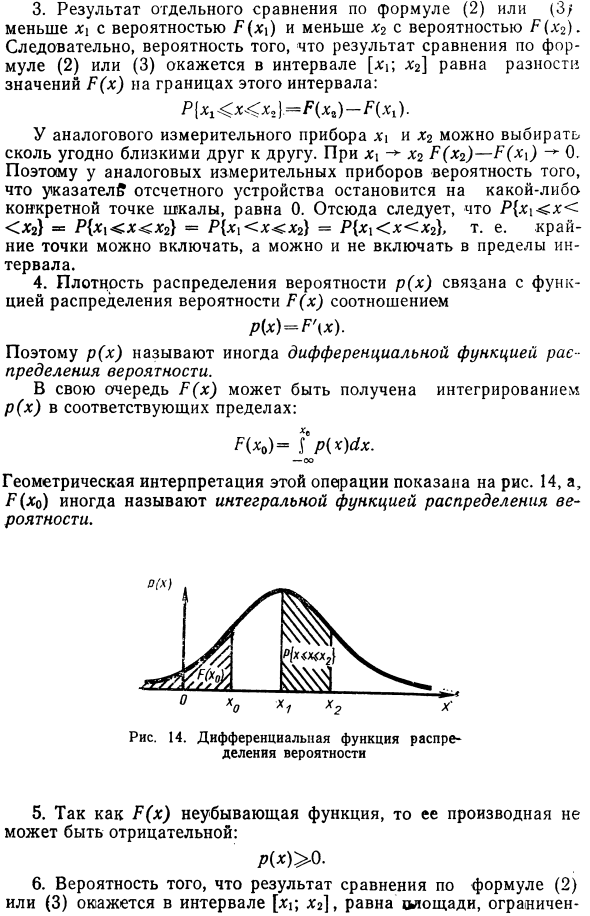
Таким образом, для аналоговых приборов вероятность того, что указатель считывающего устройства остановится в определенной точке шкалы, равна нулю. Следовательно, P x \ . X xr = P X x x2 = P x x x2 = P x1 x x2 , то есть экстремальные значения могут или не могут быть включены в интервал Есть. 4. Плотность вероятности p (x) связана с функцией распределения вероятности P (x) следующим соотношением: p (x) = P (xY Следовательно, p (x) также называется дифференциальной функцией распределения вероятностей. Аналогично, P (x) может быть получено путем интегрирования p (x) в соответствующих пределах. П (Хо) — /> (*) ** Геометрическая интерпретация этой операции показана на рисунке.
Микрометр имеет растровый преобразователь 1 и электронный блок 2 с выходом для передачи информации в систему управления. Людмила Фирмаль
Также называется интегральной функцией распределения вероятностей. Рисунок 14. Дифференциальная функция распределения вероятностей 5. P (x) — неубывающая функция, поэтому ее производная не может быть отрицательной. /> (X)> 0. 6. Результат сравнения по уравнению (2) или (3) находится в диапазоне x2; x2 , равен и ограничен График перпендикулярно Пей в функции р (х), горизонтальной оси и границы интервала (см. Рисунок 14): x x,) = р (х) с1х. 7. Увеличение интервала на неопределенный срок делает данное событие достоверным. Следовательно, площадь, ограниченная графиком функции p (x) и горизонтальной осью, равна 1. p (x) c1x = 1.
Написание ссылок с использованием законов распределения вероятностей является наиболее полным, но неудобным. Во многих случаях они ограничиваются приблизительным описанием закона распределения эталонных вероятностей с использованием их числовых свойств или моментов. Все они представляют средние значения, и когда значения, отсчитанные от начала координат, усредняются, момент называется начальным, а когда он центрирован от центра закона распределения, он называется моментом. Общие правила формирования начальных моментов: V = xG p (x) Lx, Где r — количество моментов.
Наиболее важной отправной точкой является первый средний * = ^ P (x) 0x. Это характеризует математическое ожидание в расчете на бесконечную итерацию процедуры сравнения в соответствии с уравнением (2) или (3). Возможно, будет удобнее обозначить это символом M (x). Характеристики математических ожиданий: 1) Неслучайным математическим ожиданием является именно это число: M (a) = a, где a = const1; 2) Постоянный коэффициент может быть извлечен из математического символа ожидания.
Математическое ожидание алгебраической суммы независимых случайных чисел равно алгебраической сумме математического ожидания: M (x + y — r) = M (x) 4-M (y) -M (g); 4) Математическое ожидание произведения независимых случайных чисел равно произведению этих математических ожиданий: M (x.r.g) = M (x) -M (p) .M (g); 5) математическое ожидание отклонения случайного числа от математического ожидания равно нулю: М х — М (х) = 0. Второй центральный момент служит мерой дисперсии результата сравнения согласно уравнению (2) или (3), близкому к среднему значению задания.
Общее правило формирования центрального момента записывается следующим образом: (X ^) = Uh ~ x) p (x) 0x, Из этого сразу видно, что начальный центральный момент равен нулю. x-x = (x-x) p (x) dx =; xp (x) ax-x p x) (1x = x-x 1 = 0. Второй центральный момент называется дисперсией и обозначен *. o = (^) ^ (x- ~ xUr (x) Ох. Может быть более удобно указывать дисперсию с символом O (x).
Дисперсионные характеристики: 1) Неслучайная дисперсия равна нулю: O (a) = 0, где a = const ; 2) Постоянный коэффициент может быть взят из символа отклонения, но он возводится в квадрат: O (ах) = а О (х); 3) Дисперсия алгебраической суммы независимых случайных чисел равна арифметической сумме этих дисперсий: O (x + y-r) = O (x) + E (y) + O (g); 4) Дисперсия случайного числа равна разнице между значением квадратного математического ожидания и значением квадратного математического ожидания: O (x) = M (x2) -M2 (x). минут Чем больше дисперсия, тем больше дисперсия результатов сравнения для x (2) и (3). Это хорошо видно на рисунке.
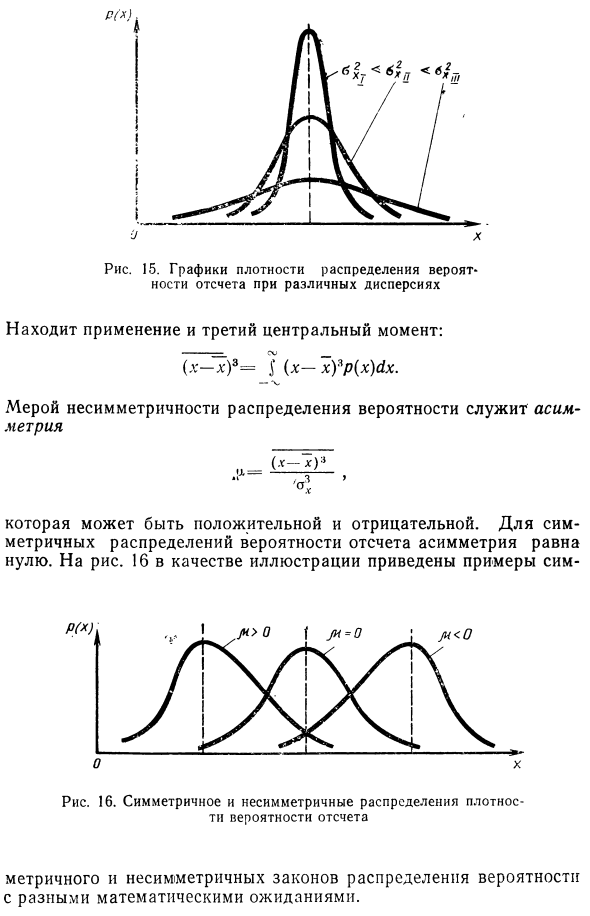
На рисунке 15 показана та же кривая плотности закона для распределения опорных вероятностей при различных дисперсиях. При измерении стандартное отклонение часто используется в качестве меры рассеяния. — + КИ. Третья центральная точка также находит применение. (X-7) 8 = (x-x) 3p (x) 0x. Мера асимметрии в распределении вероятностей — асимметрия Это может быть положительным или отрицательным. Для симметричного эталонного распределения вероятностей асимметрия равна нулю.
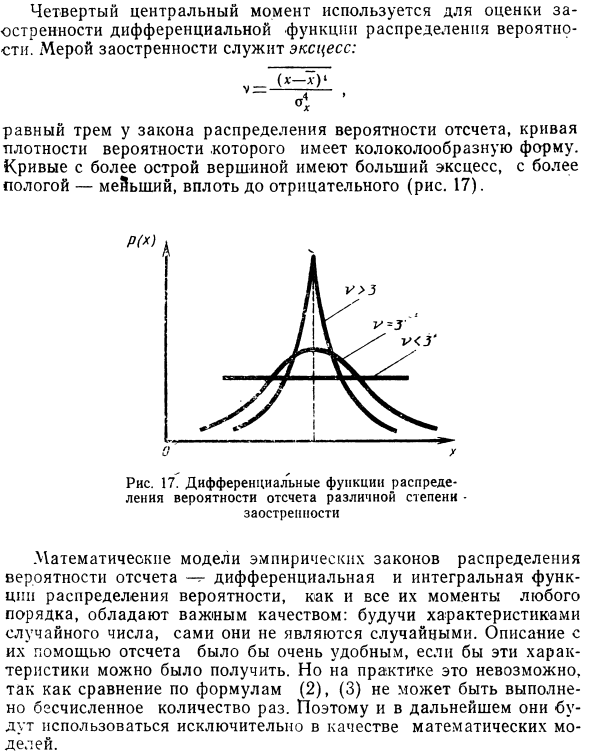
Вот пример из рисунка 16 Рисунок 16. Симметричное и асимметричное вычисление опорных вероятностей Метрический и асимметричный закон распределения вероятностей с различными математическими значениями ожидания. Четвертый центральный момент используется для оценки резкости дифференциальной функции распределения вероятностей. Мера резкости чрезмерна. Эквивалентно трем кривым плотности вероятности, которые являются законами эталонного распределения вероятностей.
Кривые с более острыми пиками больше и имеют более плоские минимумы, максимумы и максимумы и отрицательные значения (рис. 17). Рисунок 17 Дифференциальная функция распределения Он был остроконечный предмет Эвристическая математическая модель распределения эталонных вероятностей — дифференциальных и интегральных функций распределения вероятностей, а также всех моментов всех порядков, обладает важными свойствами: случайными характеристиками, а не случайными , Учитывая эти характеристики, объяснения со ссылками очень полезны. Однако на практике это невозможно, поскольку существует бесчисленное множество сравнений с использованием уравнений (2) и (3).
Поэтому в будущем По математике Они используются исключительно. Показывает одну и ту же кривую плотности закона распределения эталонных вероятностей при разных дисперсиях.
Смотрите также:
| Разновидности измерении | Учет влияющих факторов |
| Средства измерений | Исключение ошибок |
