Оглавление:


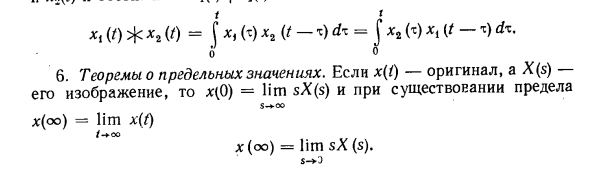

Предмет теория автоматического управления тау
| Об основных законах управления | Формы записи линейных дифференциальных уравнений. Передаточные функции |
| Уравнения динамики и статики. Линеаризация | Частотные характеристики |
Основные свойства преобразования Лапласа
- Основные свойства преобразования Лапласа Этот раздел предоставляет основную информацию из преобразования Лапласа. Это используется для изучения систем, написанных в линейных дифференциальных уравнениях. Преобразование Лапласа называется отношением и X (s) = и Это связывает функцию x (t) действительной переменной с функцией X (s) комплексной переменной s (s = o H- / co). Кроме того, x (t) называется оригиналом, а X (s) — это изображение Лапласа или изображение.
Иногда используется символическая запись X (s) = Z, \ x (t) \, Где L — оператор Лапласа. Предполагается, что функция * (/), которая подвергается преобразованию Лапласа, имеет следующие характеристики: x (/) является исходной функцией, ((«) 1. (I — I) L \ x (/) / = snX (s) -sn ~ lx (0) -s» — * x (0) —— X (0), где (А) (футы) x (0) = lim x (/), k = 0, 1 ….. / i-l. / — ♦ 4-0 / я — я Если начальное условие равно нулю, то есть x (0) = x (0) = … = x (0) = 0, Последнее выражение имеет следующий вид: L {x (t)} = snX (s).
Тот факт, что изображение X (s) из x (/) или исходный X (s) является x (t), описывается как: x (t) = X (s) или X (s) = x (t). Людмила Фирмаль
Таким образом, если начальное условие равно нулю, исходная производная соответствует изображению, умноженному на s. 3. Оригинальная интеграция. Исходная интеграция разделит изображение на s. J x (t) dt \ = T L Х (секунд) 4. Теорема о задержке. Любое положительное число м L [x (t — *)) = e˜s˜L | x (0) = e− ^ X (s). 5. Теорема о свертке (теорема умножения изображений). Если *, (/) и x2 (t) являются оригинальными, а A ‘, (s) и X2 (s) являются их изображениями, // X, (S). X, (S) = f (t) x2 (t − T = j′x2 (t) Xf (/ — T) dx. Ах ах Интегрирование в правой части уравнения называется сверткой функций x (t) и x2 (/), x, (/)> | <x. , (/). t t Xl (0 * * 2 (0 = J W (‘-X) dx = j (x) (/ -X) rfx. 6.
Ограничить значение теоремы. Если * (/) — оригинал, а X (s) — изображение, * (0) = lim sX (s) и существуют ограничения S — + — 00 x (oo) = lim x (f) T- * Co x (oo) = lim sX (s). S- + E 7. Теорема разложения. Если функция X (s) -4 (s) ‘fi (s) является дробным рациональным числом и степень полинома числителя меньше, чем степень полинома знаменателя, ее элементом является функция, умноженная на 1 (/) = Y \ r ^ -TTt I * M (* I. Где sK — корень уравнения £ (s) = 0, nh — его кратность, а / — число различных корней. Если все корни уравнения просты, эта формула разложения принимает вид N (0 = 2 B ‘(s. <) Где n — степень многочлена B (s), B ′ (sh) = 1 децибел дс с * = си
