Оглавление:

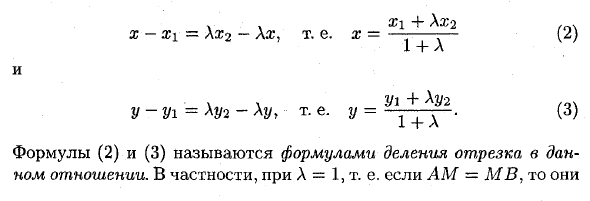


Основные задачи на метод координат (на плоскости)
- Основные задачи метода корректировки (В самолете) 1. Расстояние между двумя точками Предположим, нам нужно найти расстояние d между точками A (x \ yi) и B (x2] y2) в плоскости Oxu. Требуемое расстояние d равно длине вектора AB = (x2-®x; y2-i.e. d = \ AB \ = y / (x2-®i) 2+ (ya- »i) 2. 2. Сегментная классификация в этом отношении Предположим, что нам нужно соединить точки и разбить сегмент LP с заданным отношением A> 0.
То есть найти координаты. = Дата точки M (x \ y) на отрезке AB такая, что L. Sharp A против L, если AM-X-MB. (1) Однако AM = (x-xi; y-? / 1), то есть 4M = (x-xi) i + (2 // yi) j и JVf B = (x2-x \ y2-y), т.е. MB = (X2-x) r + (y2-y) j. Уравнение (1) принимает вид {x — x ) i + (y — y ) j = \ {x2-x) i + \ (y2-y) j. Предполагая, что координаты равных векторов равны:x-x \ — \ x2-lg, т.е. x = Xl_ + (2) 1 + А и \ \ 2/1 «b alpha / q \ Y-2 / i = Ajfe-A * / r, т.е. 2 / = 1 + q1 (3) . В частности, если A = 1, то есть AM = MV,
В этом отношении уравнения (2) и (3) называются уравнениями сегментации Людмила Фирмаль
| Выражение смешанного произведения через координаты. Применение смешанного произведения | Преобразование системы координат |
| Система координат на плоскости | Уравнение линии на плоскости, примеры |
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- x =, Tl 2 «X2’1 Y = ~ 2 Средняя точка отрезка AB. Примечание. Если A = 0, это означает, что точки A и M совпадают, а если A <0, точка M находится вне сегмента AB, точка M разделяет сегмент AB наружу ( А. в В противном случае = = т.е. AM 4-MB = 0, т.е. AB = 0). 3. Треугольник Предположим, нам нужно найти площадь треугольника ABC с вершинами A (x \ y ), B (X2 \ Y2) -> C (x3 \ Uz).
Перетащите перпендикулярные прямые AA \ A BB \, CC \ на оси Ox из вершин A, B, C (см. Рисунок). Очевидно, что в SABC = SAAiBBi + SbxBCCi для SAiACC-i. так о A, WU С1 х C 2/1 + 2/2 / 4, 2/2 + 2/3 ,, 2 / i + 2 / s / v SABC = — (s2-®i) + —— (& 3-S2) — (- (π: s-) = _ 1 5 (2: 22 / 1- + 3: 22/2-Si2 / 2 + ^ 32 / 2-222 / 2 + 232 / 3- -Z22 / 3-2: 32/1 + 2: я? / I-XzUz + ®! Уз) = = ^ (2: 3 (2 / 2-2 / 0 -2: 1 (2/2-й)) -2: 2 (2/3 2/1) +2: 1 (2 / 3-2 / 1)) = = 5 ((2 / 2-2 / 0 (2: с-2: 1) — (2 / 3-2 / 0 (2: 2-2: 1))) = i .Tz-X \ X’2-2: 1 2 / с-2/1 2 / 2-2 / 1 £ 3-XI X2-2: 1 2 / 3-2 / 1 2 / 2-2 / 1 _ 1 Это Примечание.
Если при расчете площади треугольника вы получаете 5 = 0, это означает, что точки A, B, C находятся на одной прямой, и если вы хотите получить отрицательное число, вам нужно взять его модуль средство. Людмила Фирмаль
