Рассмотрим основные свойства определенного интеграла, считая функцию 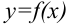 непрерывной (и, следовательно, интегрируемой) на отрезке
непрерывной (и, следовательно, интегрируемой) на отрезке 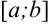 .
.
1. Постоянный множитель можно выносить за знак определенного интеграла:
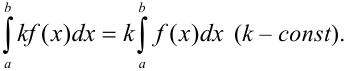
Докажем это свойство. По определению 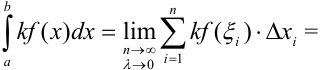
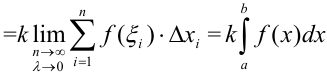 , что и требовалось доказать.
, что и требовалось доказать.
2. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме их интегралов: 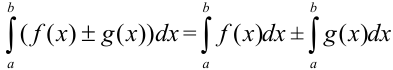 .
.
3. Границы интегрирования можно менять местами, при этом знак «минус» выносится вперед: 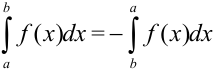 .
.
Свойства 1,2 и 3 широко применяются при вычислении определенных интегралов.
4. Определенный интеграл с одинаковыми пределами интегрирования равен нулю: 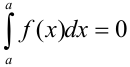 .
.
5. Если функция 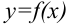 интегрируема на отрезке
интегрируема на отрезке 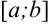 и
и 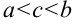 , то справедливо равенство:
, то справедливо равенство: 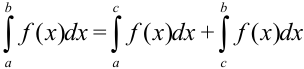 .
.
Это означает, что интеграл по всему отрезку равен сумме интегралов по его частям.
Данное свойство называют свойством аддитивности определенного интеграла.
6. Если функция 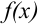 сохраняет знак на отрезке
сохраняет знак на отрезке 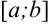
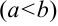 , то интеграл
, то интеграл 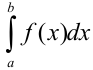 имеет тот же знак, что и функция
имеет тот же знак, что и функция 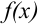 . Так, если
. Так, если 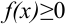 на отрезке
на отрезке 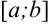 , то и
, то и 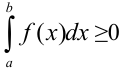 .
.
7. Неравенство между интегрируемыми функциями на отрезке 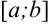
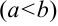 можно интегрировать: например, если
можно интегрировать: например, если 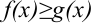 при
при 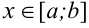 , то
, то 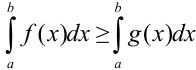 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Универсальная тригонометрическая подстановка. |
| Понятие определенного интеграла. |
| Формула Ньютона-Лейбница. |
| Применение формулы Ньютона-Лейбница. |
