Оглавление:
Основные теоремы о непрерывных функциях. Непрерывность элементарных функций
Теоремы о непрерывности функций следуют непосредственно из соответствующих теорем о пределах.
Теорема 19.1. Сумма, произведение и частное двух непрерывных функций есть функция непрерывная (для частного за исключением тех значений аргумента, в которых делитель равен нулю).
Пусть функция  и
и 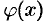 непрерывны на некотором множестве;
непрерывны на некотором множестве; 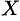 и
и 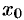 — любое значение из этого множества. Докажем, например, непрерывность произведения
— любое значение из этого множества. Докажем, например, непрерывность произведения 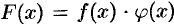 . Применяя теорему о пределе произведения, получим:
. Применяя теорему о пределе произведения, получим:
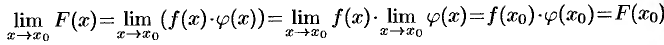
Итак, 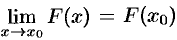 , что и доказывает непрерывность функции
, что и доказывает непрерывность функции 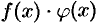 в точке
в точке 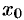 .
.
Теорема 19.2. Пусть функции 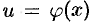 непрерывна в точке
непрерывна в точке 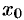 , а функция
, а функция 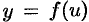 непрерывна в точке
непрерывна в точке 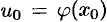 . Тогда сложная функция
. Тогда сложная функция 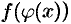 , состоящая из непрерывных функций, непрерывна в точке
, состоящая из непрерывных функций, непрерывна в точке 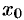 .
.
В силу непрерывности функции 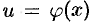 ,
, 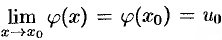 , т. е. при
, т. е. при 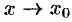 имеем
имеем 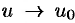 . Поэтому вследствие непрерывности функции
. Поэтому вследствие непрерывности функции 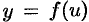 имеем:
имеем:
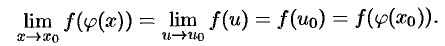
Это и доказывает, что сложная функция 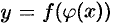 непрерывна в точке
непрерывна в точке 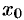 .
.
Теорема 19.3. Если функция  непрерывна и строго монотонна на
непрерывна и строго монотонна на  оси
оси  , то обратная функция
, то обратная функция 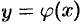 также непрерывна и монотонна на соответствующем отрезке
также непрерывна и монотонна на соответствующем отрезке 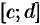 оси
оси 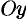 (без доказательства).
(без доказательства).
Так, например, функция 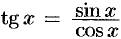 , в силу теоремы 19.1, есть функция непрерывная для всех значений
, в силу теоремы 19.1, есть функция непрерывная для всех значений  , кроме тех, для которых
, кроме тех, для которых 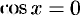 , т. е. кроме значений
, т. е. кроме значений 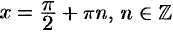 .
.
Функции 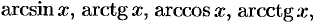 в силу теоремы 19.3, непрерывны при всех значениях
в силу теоремы 19.3, непрерывны при всех значениях  , при которых эти функции определены.
, при которых эти функции определены.
Можно доказать, что все основные элементарные функции непрерывны при всех значениях  , для которых они определены.
, для которых они определены.
Как известно, элементарной называется такая функция, которую можно задать одной формулой, содержащей конечное число арифметических действий и суперпозиций (операции взятия функции от функции) основных элементарных функций. Поэтому из приведенных выше теорем вытекает: всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Этот важный результат позволяет, в частности, легко находить пределы элементарных функций в точках, где они определены.
Пример №19-4.
Найти 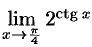 .
.
Решение:
Функция 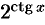 непрерывна в точке
непрерывна в точке 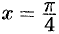 , поэтому
, поэтому
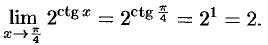
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Непрерывность функции в интервале и на отрезке |
| Точки разрыва функции и их классификация |
| Свойства функций, непрерывных на отрезке |
| Скорость прямолинейного движения |
