Оглавление:



Особенности потенциального движения жидкости
Особенности потенциального движения жидкости. Как показано выше (см. систему уравнений (4.3)), движение общей жидкости можно разбить на 3 составляющие формы.2 из них(перемещение и деформация) имеют потенциал скорости, а не в 3-м (вращение).Это разделяет движение жидкости на потенциальное (без вихря) и вихревое (без потенциала)-см. 4.1. В случае потенциального движения, охватывающего всю массу жидкости, нет вращательного движения отдельных частиц жидкости, так как в системе уравнений (4.3) компоненты вихря являются лишь результатом действия силы без потенциала, и наблюдается лишь ограниченная часть объема жидкости.
Строго говоря, потенциального движения в природе не существует, поскольку при обтекании потока твердого тела, а также при движении жидкости вдоль твердой границы канала, возникает vortex. At в то же время, при небольшой степени завихренности, можно предположить, что движение близко к потенциалу. Если предположение о потенциале оправдано, то его использование » значительно облегчает расчет основных характеристик движения. Уравнение потенциального движения может быть выражено как Интеграл Лагранжа (4.25), который имеет потенциал.
Движение реальных жидкостей будет потенциальным в тех областях, где действие сил вязкости ничтожно мало по сравнению с действием сил давления и в которых нет завихрений, образовавшихся за счёт срыва со стенок пограничного слоя или за счёт неравномерного нагревания. Людмила Фирмаль
- Скорость P, ее частная производная определяет локальную скорость МХ, Горо, iG (см. зависимости (4.21)). Для потенциального движения, уравнение неразрывности(4.27) А те|Дью / копают ’dg Дау ДХ Регулируемые друг к другу Зависимости(4.21) и поэтому、 Диг Диу лампы D2R СРБ ЦОР dh2 бы дю du2 копать РДР ДГ ~~ почтовый индекс dg2 Подставляя (4.32) в выражение (4.27), получаем: ^ почтовый индекс dg2 г Выражение(4.33) называется уравнением Лапласа, а значок V называется оператором Лапласа или набла. Если движение жидкости определяется 2 координатами (x и y) пространства, то такое движение называется плоским или 2D, и в этом случае уравнение Лапласа принимает вид: БЖ + ББ (4-34).
Если поток удовлетворяет этому уравнению, он является потенциальным. Решение уравнения Лапласа для заданного граничного условия дает семейство прямых с постоянным потенциалом скорости Р (х, г)= с,(4.35) Где C имеет постоянное значение для каждой отдельной линии потенциала постоянной скорости. Вдоль эквипотенциальной линии ^Е^ + ТГ * * −0 Или считать(4.20) Ихи + Жужу-0.(4.36) Формула (4.36) называется дифференциальным уравнением линии Изокинетического потенциала, которое часто описывается в таком виде. АУ ТС * Ди.
- Обратите внимание на исследование плоского потенциального движения на основе уравнений 6. Теория Лапласа позволяет использовать эффективные математические методы для решения гидродинамических задач (методы комфортных преобразований). При условии движения плоскости жидкости существует функция Ч ’(x, y), называемая функцией 1. Ч(х, г)= с, (4) 38) Здесь каждое значение константы C соответствует определенной линии потока. То есть, зависимость (4.38) является уравнением семейства линий тока. Вдоль линии потока Эта функция не изменяет свое значение(H ’ = sop $ 1 или c#= 0). так… а ^ = ^ ух + ^ c1y =0.
Если функция имеет постоянное значение, то разница между функциями равна базовому потоку между линиями. При сравнении (4.20) и (4.40)、 d свойствами текущей функции являются следующие условия: ,(4 42) Их Дью. Я буду. И ИУ = Дью. dh. (4.40)) Если вы назначаете (4.40) на (4.39)、 Или Это означает, что функция потока и функция потенциала постоянной скорости взаимно перпендикулярны. Рассмотрим условия невращательного движения (4.20) вместе в виде: Диди. ДХ делать. _ _iu_ ’ ДХ них (4.41) Итак, производной настоящей функции является уравнение линии потока через эту точку(4.41).
Это условие является реальным признаком ортогональности рассматриваемых кривых. Людмила Фирмаль
- Чтобы определить физический смысл разности функций потока (4.39), рассмотрим поток, который характеризуется линией потока, показанной на рисунке 5. 4.7. Согласно (4.29), скорость потока вдоль элементарного потока остается постоянной. И мы можем предположить, что Ч ’ это базовый расход между границей потока (ломаной линией) и текущей линией O, а C ^ расход между границей потока и текущей линией 1 и т. д. k и I равны разности Ch ’* Ch’.С тех пор Уравнение компоненты скорости через функцию потока(4.40). в результате、 dh. * д * у du8 = 0、 (4.43).
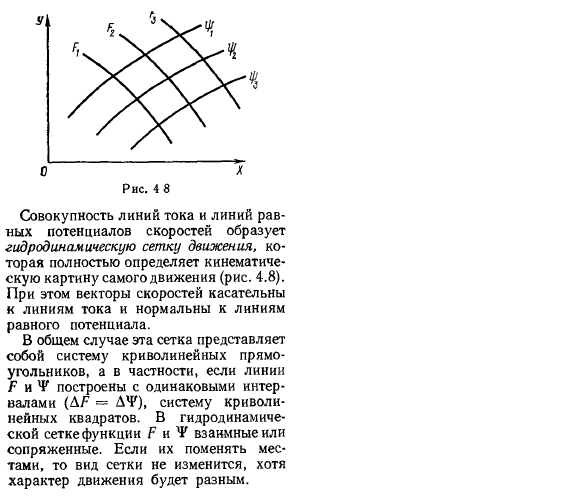
То есть текущая функция потенциального движения, такая как потенциал скорости P, Chr, удовлетворяет уравнению Лапласа. Как описано выше, обтекаемая и эквипотенциальная линии ортогональны друг другу. В соответствии с (4.41) и (4.37), угловой коэффициент этих линий Следовательно, aLag = −1. 57. Сочетание линий обтекания и потенциала постоянной скорости образует гидродинамическую сетку движения, которая полностью определяет кинематическую картину самого движения(рис.4.8). в этом случае вектор скорости является касательным к обтеканию и перпендикулярным к линии эквипотенциала.
Смотрите также:
Возможно эти страницы вам будут полезны:
