Оглавление:
Вопрос №1 «ЛЕТАЮЩИЙ БУБЛИК»
В дверях кафедры показалась рыжая голова Алексея Игнатьева, студента II курса мехфака.
Все, кто был на кафедре, лукаво улыбнулись, а Леднёв, как всегда, с ехидцей, произнёс: «Держись, Степаныч, не боись!».
- Николай Степанович, можно с вами поговорить?
- Ну что с тобой поделаешь, проходи, садись. Что тебя опять беспокоит?
Алексей подвинул стул, сел, разложил на столе листки с какими-то расчётами.
- Вот вы, Николай Степанович, на лекции доказывали, что, как следует из теоремы о движении центра масс, внутренние силы не могут заставить тело двигаться. Приводили в пример какие-то машины Дина. Который якобы доказывал, что его машины могут двигаться в пространстве за счёт вращения эксцентриков, создающих внутренние силы инерции …
- Конечно, Алёша, это чепуха. Хотя, вообще-то, не надо забывать, что внутренние силы могут вызвать появление внешних сил, которые и заставят тело или конструкцию, целую машину, перемещаться, например, по неподвижной поверхности. Возьмём автомобиль. Давление газа на днища поршней в цилиндрах двигателя — внутренние силы. Но через посредство трансмиссии они вызывают появление сил трения от дороги, действующие на колёса. Это уже внешние силы. Они и будут создавать силы, двигающие автомобиль. Но, конечно, в космосе или просто на гладкой поверхности этих сил трения не будет. И, как бы быстро колёса не вращались, автомобиль и с места не стронется.
- Вот-вот, — перебил Алексей, — а я хочу доказать… и на простой конструкции, что и внутренние силы могут вызвать движение тела. Даже по абсолютно гладкой поверхности. Смотрите…
Алексей показал листок, на котором изображено что-то вроде бублика -кольцо, половинки, которого были трубками разного диаметра (см. рисунок).
- Внутри находится мотор, который гонит жидкость по этому кольцу. В левой половинке, где диаметр больше, скорость жидкости —
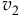 в правой —
в правой —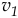 . Конечно,
. Конечно, 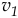 больше чем
больше чем 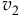 , так как по закону непрерывности струи, количество жидкости, протекающей в сечениях за секунду, должно быть одинаково:
, так как по закону непрерывности струи, количество жидкости, протекающей в сечениях за секунду, должно быть одинаково: 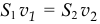 или
или 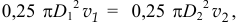 , то есть
, то есть 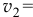
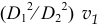 .
.
- Так, интересно… Ты, оказывается, и в физике, гидродинамике, разбираешься, молодец. И что же получается? Силы инерции в этих половинках окажутся разными? Верно?
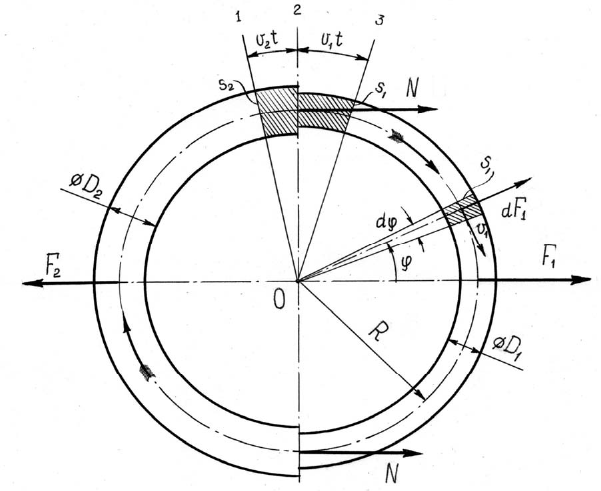
Ну, да… Смотрите. Возьмём в правой трубке малую часть жидкости объёмом
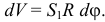
На неё действует центробежная сила инерции
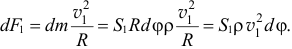
Здесь 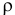 — плотность жидкости.
— плотность жидкости.
Равнодействующую сил инерции частиц всего объёма жидкости в правой трубке найдём как определённый интеграл для 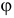 от
от 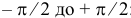 :
:
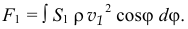
Правильно, Алексей. Полукольцо имеет ось симметрии, поэтому составляющие сил инерции, перпендикулярные этой оси, будут уравновешиваться. И чему же равна эта сила? Давай без подробностей.
Она будет равна
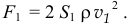
Так. А сила, действующая на левую, более толстую половинку кольца, наверное, получится аналогичной:
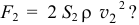
Верно?
-Да, да! А разность между ними будет равна

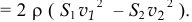
И, подставив значения площадей сечений 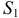 и
и 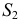 и зависимости между скоростями, получим:
и зависимости между скоростями, получим:
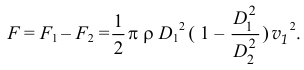
А так как 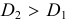 , то
, то 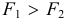 , силы не уравновешиваются и это кольцо будет двигаться поступательно под действием внутренних сил! Здорово!
, силы не уравновешиваются и это кольцо будет двигаться поступательно под действием внутренних сил! Здорово!
Гениально! Ты уверен, что ничего не забыл, что всё учёл?
Конечно! Я даже обратил внимание, что, чем больше диаметр толстой половины, тем больше будет эта сила 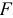 .
.
Всё это так… Но почему ты не веришь законам механики? Я о тебе был лучшего мнения. Ты, Алексей, просто забыл учесть силы, действующие на трубки в местах их соединения. Давай вернёмся к твоему чертежу. Рассмотрим верхнее сочленение. Выделим малый объём жидкости между сечениями 1 и 2. За время 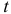 он перейдёт в правую трубку и займёт положение, ограниченное сечениями 2 и 3.
он перейдёт в правую трубку и займёт положение, ограниченное сечениями 2 и 3.
Количество движения этого объёма жидкости в первом положении
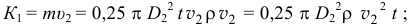
во втором положении этого объёма, в трубке малого сечения,
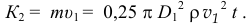
По теореме об изменении количества движения в проекции на ось
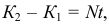
где 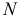 — давление на жидкость в этом сочленении со стороны трубки. Значит,
— давление на жидкость в этом сочленении со стороны трубки. Значит,
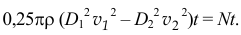
Или
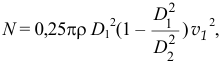
а вектор его направлен вправо. Соответственно реакция жидкости на трубку будет направлена в противоположную сторону, влево. То есть жидкость, как бы упираясь в левую половинку «бублика», продавливается в более тонкую трубку.
Если таким же образом рассмотреть движение жидкости в нижнем сочленении, получим там давление 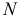 на жидкость такой же величины и направленным также вправо. В этом месте сила
на жидкость такой же величины и направленным также вправо. В этом месте сила 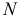 будет придерживать жидкость, заставит её уменьшить скорость. А реакция жидкости на трубку опять будет направлена влево. Сложив эти две силы, получим
будет придерживать жидкость, заставит её уменьшить скорость. А реакция жидкости на трубку опять будет направлена влево. Сложив эти две силы, получим
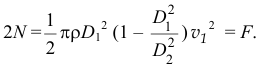
То есть они будут уравновешивать найденную выше силу инерции. Бублик останется в равновесии!
- Ну, Николай Степанович, опять вы разочаровали меня… Я-то надеялся, если не на открытие в науке, то хотя бы на ценное изобретение… Шучу, конечно…
- Увы, Алёша, к сожалению твоему, все законы механики точны и не оставляют места чему-то противоестественному. А вообще-то ты молодец, — сказал Николай Степанович, прощаясь. — Сомневаться — это хорошо. В конце концов, ты найдёшь какую-нибудь интересную тонкость в науке и используешь её для большого дела, открытия.
Вопрос №2 «ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ ТВЁРДОГО ТЕЛА»
Николай Степанович шёл по коридору после лекции перепачканный мелом. Хотелось поскорее добраться до кафедры и привести себя в порядок. Но студенты шли потоком во всех направлениях. Некоторые здоровались, уступали дорогу, а большинство не обращало на него ну никакого внимания — шумели, толкали словно незнакомого, постороннего, хотя совсем недавно слушали его лекции, сдавали экзамены и зачёты. А некоторые даже несколько раз.
Николай Степанович даже обрадовался, увидев Алексея: наверняка сейчас что-нибудь спросит, но хоть проведёт через эту неуправляемую массу толкающихся тел.
- Николай Степанович! Здравствуйте, а я как раз к вам шёл. Хотел маленький вопросик задать.
- Знаю я твой «маленький вопросик»! Ты специалист по таким «вопросикам» … Лучше проведи меня до кафедры через эту толпу жаждущих знаний …
Вымыв руки и отряхнув мел с рукавов, Николай Степанович посадил рядом Алексея: « — Ну, что у тебя?»
Вот мы с ребятами недавно спорили и не смогли объяснить, почему аптекарские весы при равновесии устанавливаются горизонтально. Ведь плечи одинаковых сил тяжести чаш с гирями и грузом всегда равны, значит, равновесие должно быть не только в горизонтальном положении.
А! Этот вопрос частенько возникает. И не только у вас, студентов. Даже преподаватели не сразу догадываются в чём дело. А ведь всё очень просто. Вы обратили внимание на то, что точки, где подвешены чаши весов, и точка, вокруг которой вращается рычаг, не расположены на одной прямой? Вот посмотри на рис. 2.1, а. В положении равновесия, когда рычаг 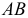 горизонтален, плечи сил одинаковы, равны
горизонтален, плечи сил одинаковы, равны 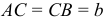 . Если же рычаг повернуть на угол
. Если же рычаг повернуть на угол 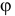 (он займёт положение, изображенное штриховыми линиями), плечи окажутся разными, обозначая
(он займёт положение, изображенное штриховыми линиями), плечи окажутся разными, обозначая 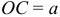 :
:

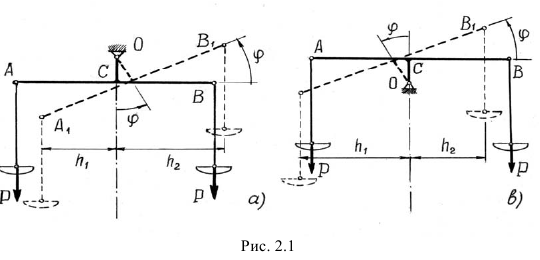
Плечо 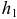 будет меньше
будет меньше 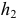 . И моменты сил станут не равными. Правая чаша весов
. И моменты сил станут не равными. Правая чаша весов 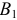 потянет рычаг вниз, угол
потянет рычаг вниз, угол 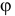 окажется по другую сторону горизонтали, плечо
окажется по другую сторону горизонтали, плечо 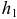 станет больше
станет больше 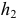 . Вращение начнётся в другую сторону. После нескольких колебаний рычаг практически при наличии сил трения займёт горизонтальное положение
. Вращение начнётся в другую сторону. После нескольких колебаний рычаг практически при наличии сил трения займёт горизонтальное положение
Обрати внимание, Алёша, если шарнир 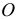 находится ниже прямой
находится ниже прямой 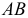 и рычаг вывести из горизонтального положения, то левое плечо
и рычаг вывести из горизонтального положения, то левое плечо 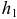 будет больше
будет больше 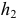
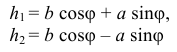
и левая чаша весов 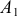 потянет рычаг вниз, против часовой стрелки. Угол
потянет рычаг вниз, против часовой стрелки. Угол 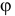 станет увеличиваться ещё больше и ни о каком равновесии говорить не придётся.
станет увеличиваться ещё больше и ни о каком равновесии говорить не придётся.
- Теперь понятно, — сказал Алексей, — оказывается, действительно, всё довольно просто.
- Ты, Алёша, затронул очень интересный и очень важный вопрос — об устойчивости положения равновесия твёрдого тела. Вот в первом рассмотренном нами случае равновесие весов было устойчиво: если рычаг вывести из горизонтального положения, он вновь вернётся в первоначальное положение. Во втором случае, если отклонить рычаг от такого же равновесного горизонтального положения даже на очень малый угол, он уже никогда не вернётся в горизонтальное положение, угол будет увеличиваться. Равновесие окажется неустойчивым.
К сожалению, в нынешних учебниках по теоретической механике, да и вообще в прикладной механике, почему-то никто не рассматривает этот очень важный для практики вопрос.
Если хочешь, Алёша, приходи к нам на кафедру в следующий четверг на методический семинар. Там мы об этом будем говорить.
- Спасибо, Николай Степанович, я приду и, если можно, приведу ещё двоих…
- Приходите.
Сообщение Николая Степановича на методичес ком семинаре кафедры теоретической и прикладной механики
Как следует из курса теоретической механики, твёрдое тело будет неподвижным, в состоянии покоя или равновесия, если выполняются два условия: главный вектор сил, приложенных к телу (векторная сумма сил), равен нулю,
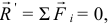
и главный момент сил (векторная сумма моментов сил относительно любой точки) тоже равен нулю,
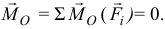
Что произойдёт с этим телом, если в некоторый момент оно изменит своё положение: повернётся на малый угол или переместится в другое близкое место? Вернётся оно в первоначальное положение или равновесие нарушится, и тело начнёт удаляться от положения равновесия? То есть устойчиво было равновесие тела или неустойчиво?
Предполагая время выхода тела из равновесного состояния достаточно малым, можно считать, что точки приложения сил к телу и направление векторов сил относительно неподвижной системы не изменились. Естественно, главный вектор R’ останется прежним, равным нулю. Но главный момент М0 изменится, так как плечи сил будут другими, станет не равным нулю. Тело начнёт вращаться под действием появившейся пары сил.
Если эта пара будет стремиться вернуть тело в прежнее равновесное состояние, равновесие считается устойчивым. Если же она будет направлена в сторону, в которую началось вращение, и тем самым будет удалять тело от первоначального положения, то такое равновесие тела следует считать — неустойчивым.
В этом легко убедиться, рассмотрев, например, равновесие тела под действием двух сил. Такие силы, конечно, равны по модулю и направлены по одной прямой в противоположные стороны. Но они могут оказывать на тело разное действие в зависимости от взаимного направления: либо будут сжимать тело, либо растягивать. В первом случае, при сжатии, равновесие будет неустойчивым; во втором, при растяжении, устойчивым. Это довольно очевидно, достаточно повернуть тело на малый угол в любом направлении.
Итак. Об устойчивости равновесия твёрдого тела можно судить лишь по поведению главного момента сил, приложенных к телу.
Пусть тело, находящееся в равновесии, повернулось вокруг некоторой оси  , перпендикулярной плоскости чертежа, на малый угол
, перпендикулярной плоскости чертежа, на малый угол 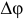 , например, против часовой стрелки (рис. 2.2).
, например, против часовой стрелки (рис. 2.2).
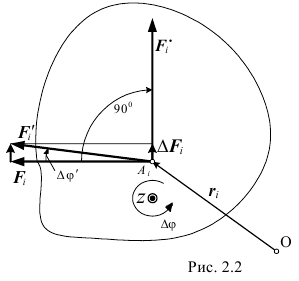
Только в дальнейшем для удобства математического анализа положим, что не тело, а силы повернулись вокруг точек приложения на одинаковые углы 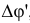 , равные
, равные 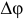 , но в противоположном направлении.
, но в противоположном направлении.
На рисунке показана только одна из всех сил, сила  . Её повернули вокруг точки приложения
. Её повернули вокруг точки приложения 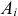 , и она заняла положение
, и она заняла положение 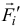 , изменившись на вектор
, изменившись на вектор 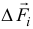 такой, что
такой, что 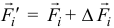 . Изменение силы при малом угле
. Изменение силы при малом угле 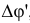 можно считать по модулю равным
можно считать по модулю равным 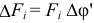 и направленным перпендикулярно
и направленным перпендикулярно 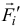 в сторону поворота силы.
в сторону поворота силы.
Найдём теперь сумму моментов повёрнутых сил  — относительно некоторой точки
— относительно некоторой точки 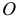 , то есть момент
, то есть момент 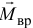 соответствующей пары сил:
соответствующей пары сил:
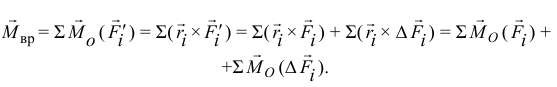
Но первая сумма здесь — есть главный момент заданных сил. Она равна нулю по условию равновесия. Значит момент вращающей пары 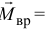
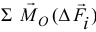 равен лишь сумме моментов добавленных сил
равен лишь сумме моментов добавленных сил 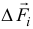 .
.
Повернём теперь заданные силы  вокруг точек приложения по направлению
вокруг точек приложения по направлению 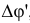 на угол 90° (см. рис. 2.2). Они займут положения
на угол 90° (см. рис. 2.2). Они займут положения 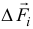 , совпадающие с
, совпадающие с 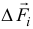 . Поэтому можно написать:
. Поэтому можно написать:
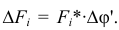
Тогда момент вращающей пары
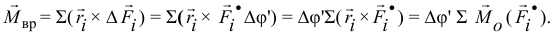
Если эта пара, определяемая суммой моментов повёрнутых на 90° сил стремится повернуть тело в начальное, равновесное, положение, то есть будет направлена по стрелке угла 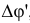 то равновесие тела следует считать устойчивым. Если в противоположную сторону — неустойчивым.
то равновесие тела следует считать устойчивым. Если в противоположную сторону — неустойчивым.
Теперь можно сформулировать теорему, правило определения устойчивости равновесия твёрдого тела.
«Нужно заданные силы повернуть на 90° вокруг точек приложения, вокруг параллельных осей, в каком-нибудь направлении и определить сумму моментов повёрнутых сил относительно какой-либо точки, то есть найти момент соответствующей пары  .
.
Если эта пара будет стремиться повернуть тело в том же направлении, в котором повёрнуты силы, то равновесие тела устойчиво.
Если в противоположном направлении или при 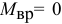 , равновесие -неустойчиво»
, равновесие -неустойчиво»
Замечания.
- Если на тело действуют силы произвольно расположенные, то следует проверить устойчивость равновесия при повороте вокруг трёх взаимно перпендикулярных осей. Предварительно надо разложить силы на составляющие, параллельные этим осям.
- Конечно, устойчивость равновесия имеет смысл исследовать только у тел, имеющих степени свободы.
Небольшой пример. Прямоугольное тело находится в равновесии под действием сил 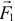 и
и 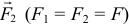 (рис. 2.3). Реакции неподвижного шарнира
(рис. 2.3). Реакции неподвижного шарнира 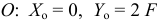 .
.
Проверим устойчивость равновесия тела. Повернём все силы на 90° против часовой стрелки. Найдём вращающий момент относительно шарнира 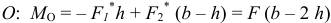 .
.

Чтобы равновесие было устойчивым, момент 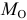 должен быть положительным, направленным против часовой стрелки, то есть чтобы выполнялось условие
должен быть положительным, направленным против часовой стрелки, то есть чтобы выполнялось условие 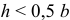 .
.
Аналогичный результат получим, конечно, определив момент сил и относительно, например, точки 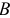 :
:
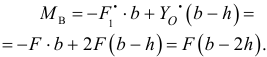
Таким же способом можно было определить устойчивость равновесия и аптечных весов, рассмотренных на рис. 2.1, а и 2.1,6.
В заключение следует заметить, что в основу данной теоремы об устойчивости равновесия твёрдого тела положена идея, предложенная ещё в сороковых годах прошлого века доцентом Ленинградского инженерно-строительного института B.C. Костроминым.
Вопрос №3 «МГНОВЕННО ИЗМЕНЯЕМАЯ СИСТЕМА»
- Николай Степанович, со мной в комнате живёт студент первого курса. Ему дали на дом задачку по статике, а он никак не может её решить. Самое смешное — и я не могу. Хвастался, что неплохо разбираюсь в теоретической механике и вот попал впросак. Чувствую, что задача какая-то странная. А в чём дело — не пойму.
- Бывает такое и нередко. Ну-ка, покажи задачку.
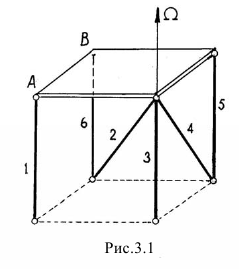
Алексей вытащил из папки лист, на котором нарисована схема пространственной конструкции, квадратная плита весом 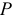 на шести стержнях (рис. 3.1), и решение задачи.
на шести стержнях (рис. 3.1), и решение задачи.
Николай Степанович посмотрел, усмехнулся и сказал:
Знакомая задача. Даже знаю в каком сборнике её взяли [9, с.42]. Там, кстати, ещё есть подобные интересные задачи. Ну и что же у вас получилось?
Да вот результат:
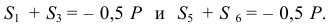
А чему они равны — не известно. Судя по ответу, все эти силы равны и равны 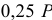 . Но ведь тут неопределённость получается. Может быть и
. Но ведь тут неопределённость получается. Может быть и 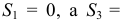
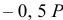 , a
, a 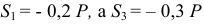 или даже
или даже 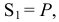 , а
, а 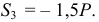
А ведь задача-то статически определимая, число неизвестных равно числу возможных уравнений равновесия!
- Ну что ж, Алёша, ты открыл одну очень интересную страницу в теоретической механике, про которую забывают даже некоторые авторы задач и, что ещё опаснее, даже разработчики строительных конструкций. Не мудрено, что такие конструкции разрушаются. Вспомни, как развалился недавно аквапарк в Москве. Хорошо, что аналогичным конструкциям в строительной механике уделяется хоть немного внимания. А в курсе теоретической механики, к сожалению, об этом вообще ничего не говорится.
Дело в том, Алёша, что кроме статически определимых и статически неопределимых систем, о которых говорится в теоретической механике, существуют ещё и мгновенно изменяемые системы, конструкции.
Это такие системы, отдельные части которых имеют возможность совершать малые перемещения, допускаемые связями. С такими перемещениями ты, Алёша, знаком. О них подробно говорилось в разделе динамики. Это — возможные перемещения.
- Конечно, вспоминаю. Был такой принцип возможных перемещений.
- Правильно. Вспомни ещё, что для плоской конструкции возможные перемещения точек определяются при повороте на малый угол вокруг мгновенного центра скоростей
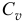 . А для пространственной конструкции -при повороте вокруг мгновенной оси вращения
. А для пространственной конструкции -при повороте вокруг мгновенной оси вращения 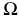 .
.
Если мгновенно изменяемая система состоит из нескольких тел, то у каждого тела должен быть свой мгновенный центр скоростей, но возможные перемещения точек контакта этих тел должны быть совместимы. Вот несколько примеров таких мгновенно изменяемых систем (рис. 3.2).
На схемах 3.2а и 3.2, 6 мгновенная изменяемость очевидна: все точки тел 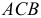 имеют возможные перемещения, определяемые мгновенными центрами скоростей. Да и у схемы 3.2, в всё понятно: возможные перемещения определяются поворотом тел вокруг шарниров
имеют возможные перемещения, определяемые мгновенными центрами скоростей. Да и у схемы 3.2, в всё понятно: возможные перемещения определяются поворотом тел вокруг шарниров 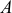 и
и 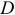 и пропорциональны. А у схемы 3.2, д легко обнаружить совместимость возможных перемещений муфты
и пропорциональны. А у схемы 3.2, д легко обнаружить совместимость возможных перемещений муфты 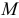 и соответствующей точки у стержня
и соответствующей точки у стержня 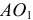 .
.
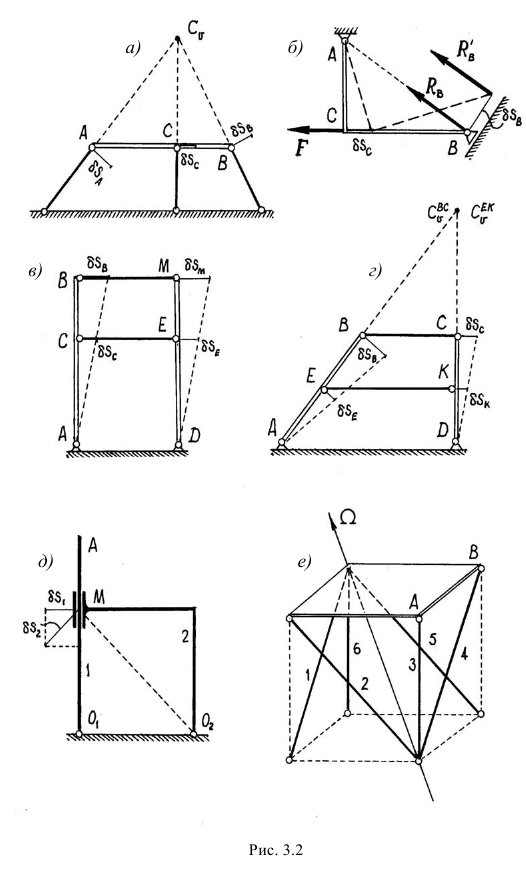
У конструкции 3.2, г, имеющей два совпадающих мгновенных центра скоростей стержней 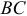 и
и 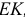 , можно доказать, что возможные перемещения точек стержней пропорциональны расстояниям до этих центров. У пространственных конструкций (3.1 и 3.2, е) легко находятся мгновенные оси вращения
, можно доказать, что возможные перемещения точек стержней пропорциональны расстояниям до этих центров. У пространственных конструкций (3.1 и 3.2, е) легко находятся мгновенные оси вращения 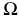 .
.
- Николай Степанович, так возможно ли какое-то решение при исследовании таких систем? Ведь конструкции-то их осуществимы.
- Если определять реакции связей таких конструкций, выявляются интересные результаты.
В конструкции 3.1 ты, Алёша, их уже обнаружил: нет решения, невозможно определить усилия в четырёх стержнях от силы 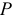 , веса плиты. А ещё интереснее получилось бы решение, если добавить ещё силу
, веса плиты. А ещё интереснее получилось бы решение, если добавить ещё силу 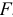 , направленную по стороне
, направленную по стороне  . Составив уравнение моментов сил относительно оси
. Составив уравнение моментов сил относительно оси 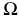 , ты обнаружил бы, что эта сила
, ты обнаружил бы, что эта сила 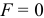 ! Так как моменты других сил, усилий в стержнях и силы
! Так как моменты других сил, усилий в стержнях и силы 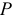 равны нулю.
равны нулю.
Такой же интересный результат получился бы и в системе 3.2, е, если приложить силу к плите, направленную по стороне  , например.
, например.
Кроме того что исследование мгновенно изменяемых систем практически невозможно, появляется ещё одна, более опасная особенность. После того, как система совершит малые перемещения, то есть несколько изменит свою форму, система станет статически определимой. Но реакции некоторых связей окажутся очень большими и конструкция может разрушиться.
Если хочешь, Алёша, можешь проверить и убедиться, что это так. Например, дай малое перемещение уголку 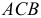 на схеме 3.2, 6 (это положение показано штриховыми линиями) и составь уравнение моментов, при
на схеме 3.2, 6 (это положение показано штриховыми линиями) и составь уравнение моментов, при 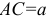
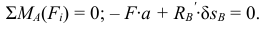
Получим
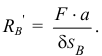
Перемещение 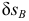 очень мало. Значит реакция
очень мало. Значит реакция 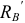 получится очень большой.
получится очень большой.
- Так как же проверить систему на мгновенную изменяемость? Только так, как вы, Николай Степанович, сейчас показали? Или существуют другие методы и способы?
- Можно использовать некоторые специальные признаки. Есть одна довольно интересная статья [1] в сборнике научно-методических статей по теоретической механике, опубликованной ещё в 1981 г., в которой автор Александров В.В. доказал, что если определитель системы уравнений, составленный из коэффициентов при неизвестных, окажется равным нулю, то такая система является мгновенно изменяемой. Конечно, если число неизвестных равно количеству уравнений равновесия.
Если хочешь, можешь проверить, исследовав схемы на рис. 3.2. Все определители окажутся равными нулю.
- Да, нет. Я верю, Николай Степанович. А как можно исправить такую мгновенно изменяемую конструкцию, чтобы она могла работать?
- Надо лишь немного изменить её конструкцию, изменить углы или размеры. Вот, например, в схеме 3.2а — изменить направление хотя бы одного какого-нибудь стержня так, чтобы они не пересекались в одной точке.
В схеме 3.2, в можно изменить длины балочек 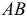 и
и 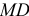 . Например, шарнирную опору
. Например, шарнирную опору 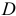 опустить ниже.
опустить ниже.
- Ну, спасибо, Николай Степанович. Я, кажется, стал немного умнее. Пойду, расскажу всё своему соседу. Может поймёт, как интересна теоретическая механика.
Вопрос №4 «О РАБОТЕ СИЛЫ»
Николай Степанович встретил Игнатьева в коридоре.
- Ну-ка, Алёша, зайди ко мне. Есть интересное предложение.
Взял его за локоть, как старого знакомого, довёл до кафедры, усадил рядом.
- В апреле, Алёша, будет студенческая научная конференция. Если не против, я могу предложить тебе очень интересную тему. Не возражаешь?
- Да, нет. Я могу. Ещё целый месяц впереди.
- Ну и хорошо. Я сначала дам тебе маленькую, но необычную задачку. Такую даже не в каждом сборнике найдёшь. Я уже и условие приготовил. Вот смотри (рис. 4.1). Со стола спускается тяжёлая однородная нить длиной
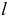 . Сначала конец её
. Сначала конец её 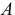 был на краю стола и нить была неподвижна. Пренебрегая всякими сопротивлениями и жесткостью нити, нужно определить, как будет соскальзывать нить со стола, как будут двигаться её точки, например точка
был на краю стола и нить была неподвижна. Пренебрегая всякими сопротивлениями и жесткостью нити, нужно определить, как будет соскальзывать нить со стола, как будут двигаться её точки, например точка 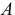 .
.
Решай задачу с помощью теоремы об изменении кинетической энергии. Только имей в виду, что работу веса свешивающейся части нити придётся находить с помощью элементарной работы, так как эта сила переменна и точка приложения её относительно нити перемещается. Ведь так? Больше ничего подсказывать не буду. Мне интересно, заметишь ли ты некоторые особенности и как ты с ними справишься. Недели тебе хватит? Ну и хорошо. Жду тебя в следующий четверг.
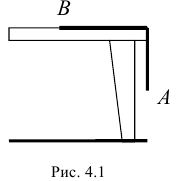
Игнатьев, как и договаривались, появился в точно назначенное время. — Вот, Николай Степанович, посмотрите, что у меня получилось. С кинетической энергией всё просто. В начале движения
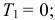
после того, как часть нити соскользнет со стола, кинетическая энергия
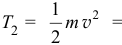
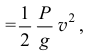
так как все точки нити имеют одинаковые скорости. Работа веса 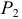 горизонтальной части нити равна нулю. А вот при вычислении работы, которую совершит вес
горизонтальной части нити равна нулю. А вот при вычислении работы, которую совершит вес 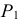 свешивающейся части, как вы и намекнули тогда, появляется что-то интересное. По правилам элементарную работу надо вычислять по формуле
свешивающейся части, как вы и намекнули тогда, появляется что-то интересное. По правилам элементарную работу надо вычислять по формуле 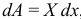 , где
, где 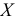 — проекция силы на ось
— проекция силы на ось 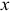 (рис. 4.2), a
(рис. 4.2), a 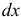 — дифференциал координаты
— дифференциал координаты 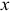 точки приложения силы, находящейся посередине свешивающейся части. Элементарная работа получается такой, имея в виду, что
точки приложения силы, находящейся посередине свешивающейся части. Элементарная работа получается такой, имея в виду, что

Проинтегрировав, получим
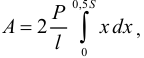
где
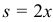
длина вертикальной части нити, или
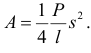
По теореме
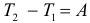
получаем уравнение
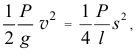
из которого находим скорость точек нити
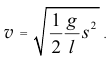
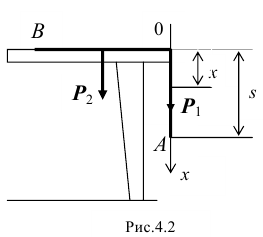
Ты, Алёша, как это кажется, действовал правильно. Но давай сделаем небольшую проверку. Когда конец В, последняя точка нити, соскользнёт со стола, то есть при 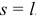 , скорость нити по твоему решению будет
, скорость нити по твоему решению будет 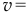
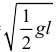 . Так? А должно получиться иначе. Ведь, когда вся нить станет
. Так? А должно получиться иначе. Ведь, когда вся нить станет
вертикальной, работа веса нити будет 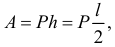 где
где 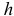 — высота, на которую опустится центр тяжести всей нити. По теореме об изменении кинетической энергии получим
— высота, на которую опустится центр тяжести всей нити. По теореме об изменении кинетической энергии получим
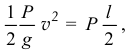
откуда
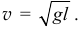
Больше, чем в твоём решении! Значит метод, которым ты решал задачу и вроде бы правильно делал, не верен!
Давай договоримся так. Я тебе дам одну статейку на эту тему. Ты её проштудируй, разберись и сделай сообщение на методическом семинаре нашей кафедры. Многим из нас это будет очень интересно. А для тебя -хорошая тренировка для будущей научной работы. Только не тяни. Студенческая конференция не за горами. Надо будет, приходи — я помогу.
Сообщение студента Алексея Игнатьева на методическом семинаре кафедры теоретической и прикладной механики
Элементарная работа силы определяется по известной формуле
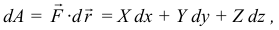
где 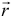 — радиус-вектор точки приложения силы;
— радиус-вектор точки приложения силы; 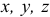 — координаты этой точки;
— координаты этой точки; 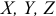 — проекции силы на оси.
— проекции силы на оси.
Но эта формула верна лишь для силы, вектор которой закреплён в точке тела. Если же точка приложения вектора силы меняет своё положение на теле, то не всё оказывается понятным. Действительно, какое в этом случае надо вычислять изменение радиуса-вектора? Абсолютное?
В сборнике научно-методических статей по теоретической механике (выпуск 11-й) [7] доказана теорема, которая даёт ответ на этот вопрос.
«Мощность некоторой силы 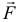 , точка приложения которой перемещается по телу, есть скалярное произведение вектора этой силы на вектор скорости той точки тела, с которой совпадает в данный момент начало вектора этой силы».
, точка приложения которой перемещается по телу, есть скалярное произведение вектора этой силы на вектор скорости той точки тела, с которой совпадает в данный момент начало вектора этой силы».
Здесь и далее для удобства доказательств и решения задач вычисляется мощность силы, с помощью которой легко определяется затем и работа силы.
Очень полезны следствия из этой теоремы.
- Если тело движется поступательно (скорости всех точек его одинаковы), то перемещение точки приложения силы по телу можно не учитывать и предполагать этот вектор закреплённым в произвольно выбранной точке тела.
- Если вектор силы перемещается по твёрдому телу вдоль определённой линии действия, то мощность, а значит и работа силы, не будут зависеть от такого перемещения, так как проекции вектора скорости точек тела на эту линию равны (см. теорему на с. 74).
Силы, точка приложения которых перемещается относительно движущегося тела, встречаются нередко. Обычно это силы трения, возникающие при скольжении одного тела по поверхности другого; сила тяжести тела переменной массы или формы; натяжение нити, намотанной на тело и некоторые другие силы. Вот несколько примеров.
Задача, предложенная Николаем Степановичем (см. рис. 4.2). Там центр тяжести, точка приложения веса 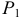 свешивающейся части нити перемещается по нити. И эта часть нити движется поступательно, поэтому точку приложения силы
свешивающейся части нити перемещается по нити. И эта часть нити движется поступательно, поэтому точку приложения силы 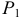 удобно перенести на конец
удобно перенести на конец 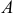 нити.
нити.
Направим ось 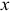 вниз и начало координат возьмём на краю стола. Тогда элементарная работа силы
вниз и начало координат возьмём на краю стола. Тогда элементарная работа силы
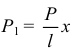
будет
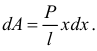
А полная работа
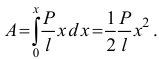
И, так как в начале движения, когда 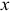 = 0, кинетическая энергия
= 0, кинетическая энергия 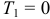 , а в промежуточном положении
, а в промежуточном положении
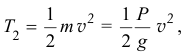
то по теореме об изменении кинетической энергии получим уравнение
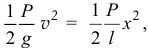
из которого находим
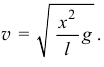
В частности, когда последняя точка нити В соскользнёт со стола, скорость точек нити будет 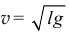 . Решение получается правильным.
. Решение получается правильным.
Ещё одна задача. Тяжёлая однородная нить длиной 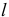 была прикреплена обоими концами к точке
была прикреплена обоими концами к точке 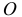 , располагалась вертикально и была неподвижна. Затем один конец её отцепился от точки
, располагалась вертикально и была неподвижна. Затем один конец её отцепился от точки 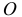 и точки правой части нити стали двигаться вниз так, что вся нить оставалась вертикальной (рис.4.3). Определим движение свободного конца нити.
и точки правой части нити стали двигаться вниз так, что вся нить оставалась вертикальной (рис.4.3). Определим движение свободного конца нити.
Начало координат возьмём в точке 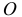 . Движение конца нити определяем координатой
. Движение конца нити определяем координатой 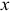 . Вес движущейся в этот момент части нити
. Вес движущейся в этот момент части нити
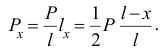
Кинетическая энергия точек нити в начале движения
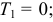
в промежуточном положении
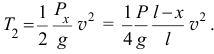
Элементарная работа веса движущейся части нити, так как она опускается поступательно
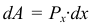
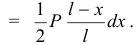
Работа веса на перемещение 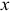
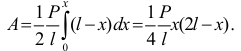
По теореме
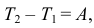
получим уравнение
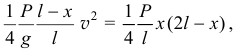
из которого находим скорость конца нити в данном положении
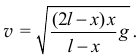
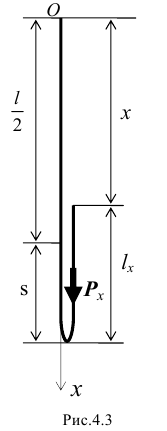
Теперь можно определить скорость конца нити в любом положении.
Николай Степанович терпеливо выслушал решение этой задачи и сделал замечание.
- Ты, Алёша, использовал теорему об изменении кинетической энергии. Но, к сожалению, в таком виде эта теорема здесь не работает, так как мы имеем дело с телом переменной массы. Так что полученный результат не верен. А вот решение первой задачи было правильным, там масса движущейся нити постоянна. Об определении движения тел переменной массы мы с тобой как-нибудь специально поговорим. Но даже при твоём не совсем правильном решении можно сделать неожиданный, но правильный вывод. Обрати внимание, что в конце движения при
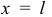 скорость
скорость 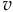 становится бесконечно большой. Правда, это очень интересно? Если ты когда-нибудь видел и слышал, как хлопают кнутом пастухи, то теперь можешь объяснить, как это у них получается. Скорость точки на конце кнута преодолевает звуковой барьер (как реактивный самолёт) и слышится резкий хлопок. Можешь сам попробовать: щёлкнуть даже коротким хлыстом с тонким концом.
становится бесконечно большой. Правда, это очень интересно? Если ты когда-нибудь видел и слышал, как хлопают кнутом пастухи, то теперь можешь объяснить, как это у них получается. Скорость точки на конце кнута преодолевает звуковой барьер (как реактивный самолёт) и слышится резкий хлопок. Можешь сам попробовать: щёлкнуть даже коротким хлыстом с тонким концом. - У меня, Николай Степанович, есть ещё один, кажется, интересный пример. Вот я нарисовал диск, который равномерно вращается с угловой скоростью
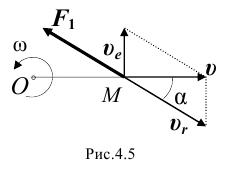
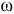 (рис.4.4), а по нему с постоянной скоростью
(рис.4.4), а по нему с постоянной скоростью 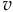 в одной плоскости с осью вращения скользит вертикальный стержень.
в одной плоскости с осью вращения скользит вертикальный стержень.
Силы трения действуют и на диск, и на стержень. Какую работу совершают эти силы?
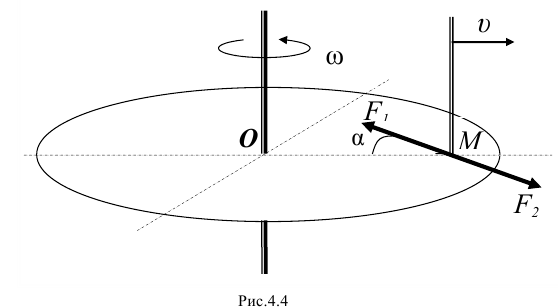
На основании первого следствия из теоремы следует показать две силы трения. Одна сила 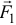 приложена к стержню, направлена в сторону, противоположную его скорости относительно вращающегося диска, и мощность её равна
приложена к стержню, направлена в сторону, противоположную его скорости относительно вращающегося диска, и мощность её равна
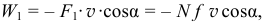
где 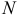 — нормальная реакция диска,
— нормальная реакция диска, 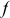 — коэффициент трения скольжения,
— коэффициент трения скольжения, 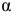 — угол между вектором скорости стержня
— угол между вектором скорости стержня 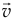 и вектором силы трения
и вектором силы трения 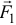 . Другая сила
. Другая сила 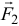 , равная и противоположно направленная силе
, равная и противоположно направленная силе 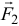 приложена к диску. Мощность её, определяемая скоростью той точки диска, на которую опирается стержень, равна
приложена к диску. Мощность её, определяемая скоростью той точки диска, на которую опирается стержень, равна
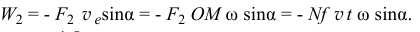
Из рис.4.5, на котором показаны скорости точки 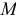 стержня, следует
стержня, следует
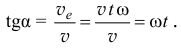
Значит,
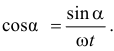
Поэтому полная мощность сил трения
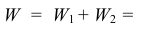
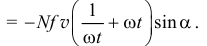
Так как
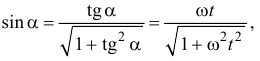
то
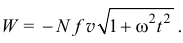
Работу сил трения на перемещении за время 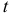 можно найти как интеграл:
можно найти как интеграл:
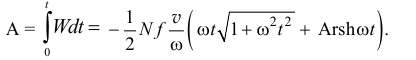
- Ну, ты, Алёша, молодец. Хорошо разобрался в этой теории. Да и высшую математику знаешь неплохо.
В заключении Николай Степанович отметил, что материал, о котором рассказал А.Игнатьев, очень интересный. И, если кто заинтересовался, пусть попробует ответить хотя бы на пару таких вопросов: будет ли совершать работу вес куска льда, поставленного на горячую сковородку и, наоборот, если испаряется только верхняя часть его; будет ли совершать работу вес пассажира, шагающего вверх по эскалатору, который движется вниз с такой же скоростью?
Вопрос №5 «ПОГОВОРИМ О СИЛАХ»
- Николай Степанович, можно задать вам, как мне кажется, довольно вредный вопрос?
- Это почему же «вредный», Алёша? Ты меня прямо напугал …
- А вот я сейчас посмотрю, как будете, извините, оправдывать сказанное на прошлой лекции. Помните, когда говорили о теореме о движении центра масс, вы доказывали, что изменить его движение могут только внешние силы. И привели два интересных примера. Мол, автомобиль движется под действием сил трения, возникающих между ведущими колёсами и дорогой, так как это единственные внешние силы, приложенные к автомобилю, которые направлены горизонтально и вперёд.
И второй пример. Что человек может подпрыгнуть только за счёт реакции, нормальной реакции поверхности, так как это единственная внешняя сила, приложенная к человеку, которая направлена вертикально вверх.
- Ну и что же тебя смущает, дорогой Алёша?
- А как объяснить, почему человек, стоящий, например, на скамейке, подпрыгивает, а скамейка остаётся неподвижной? Ведь нормальная реакция поверхности приложена в первую очередь к скамейке и будет такой же, даже большей, величины? А вот, если скамейку прикрепить к ногам человека, то она «подпрыгнет» вместе с человеком! При условии, конечно, что скамейка не очень тяжёлая. Значит, к человеку прикладывается какая-то другая сила, направленная вверх и приложенная только к человеку!
- Да, — подумав немного, сказал Николай Степанович, — это интересно. Признаться, меня самого иногда смущало такое примитивное и, казалось бы, естественное объяснение. И если уж даже для тебя такое объяснение оказывается не очень доказательным, давай попробуем во всём этом разобраться. Ты, Алёша, поднимаешь интересный вопрос.
- И ещё, Николай Степанович, эти силы, сила трения у колёс автомобиля и нормальная реакция у подпрыгивающего человека приложены к поверхностям тел в точках, скорости которых равны нулю, и работу не совершают. Об этом я докладывал как-то на методическом семинаре кафедры. Значит, эти силы не могут изменить кинетическую энергию тел, то есть не могут и заставить эти тела двигаться.
- Давай разберёмся сначала с прыгающим человеком. Тут, Алёша, нам надо рассуждать так. Рассмотрим сам процесс прыжка.
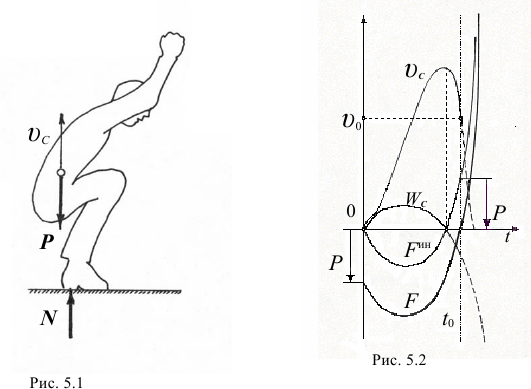
Готовясь к прыжку, человек приседает (рис. 5.1), сжимая мышцы ног и бёдер как пружины. Затем резко выпрямляется под действием силы 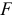 , вызванной этой «пружиной».Тело приобретает скорость центра тяжести
, вызванной этой «пружиной».Тело приобретает скорость центра тяжести 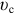 , направленную вверх. И как только, в какой-то момент
, направленную вверх. И как только, в какой-то момент 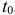 , выпрямление «пружины» закончится, туловище по инерции продолжит движение вверх, увлекая за собой и ноги, отделив их от поверхности пола.
, выпрямление «пружины» закончится, туловище по инерции продолжит движение вверх, увлекая за собой и ноги, отделив их от поверхности пола.
Таким образом, прыжок человека происходит не под действием реакции пола 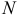 на подошвы ботинок, а вызывается «упругой» силой
на подошвы ботинок, а вызывается «упругой» силой 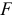 сжатых ног, приложенной к туловищу.
сжатых ног, приложенной к туловищу.
Кстати эта сила 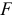 , вызывающая движение тела, порождает силу инерции его. По принципу Даламбера сила
, вызывающая движение тела, порождает силу инерции его. По принципу Даламбера сила 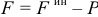 . А сила инерции определяется ускорением тела, изменением скорости. На рис. 5.2 даны графики характеристик движения. Видим, что скорость
. А сила инерции определяется ускорением тела, изменением скорости. На рис. 5.2 даны графики характеристик движения. Видим, что скорость 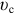 , достигнув максимума где-то в конце выпрямления ног, начнёт быстро уменьшаться. Ускорение
, достигнув максимума где-то в конце выпрямления ног, начнёт быстро уменьшаться. Ускорение 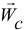 становится большим и направленным вниз, а сила инерции — вверх. И чем быстрее изменяется скорость, тем больше ускорение и сила инерции, а значит, и сила
становится большим и направленным вниз, а сила инерции — вверх. И чем быстрее изменяется скорость, тем больше ускорение и сила инерции, а значит, и сила 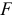 , и тем выше человек подпрыгнет.
, и тем выше человек подпрыгнет.
Так что спортсмену надо заранее хорошо потренироваться, продумать сам процесс выпрямления ног. И не так как выпрямляется обычная пружина, по гармоническому закону. А сделать так, чтобы в конце выпрямления скорость тела была как можно больше, а остановка его была бы резкой, кратковременной. Опытные спортсмены это знают и автоматически, а может инстинктивно, так и поступают.
- Мой сосед в общежитии как раз занимается прыжками. Я его познакомлю с нашими выводами. Может, они его заинтересуют и помогут в чём-то. А теперь, Николай Степанович, давайте разберёмся с движением автомобиля.
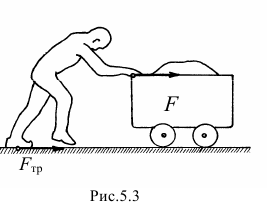
- Конечно. Но сначала, Алёша, скажи мне, какие силы двигают вагонетку, которую толкает человек. Вот посмотри на эту картинку (рис.5.3). Наверное, не сила трения
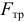 , приложенная к подошве ботинка, хотя это единственная внешняя сила действующая на систему человек-вагонетка и направленная горизонтально. Скорее всего это будет сила
, приложенная к подошве ботинка, хотя это единственная внешняя сила действующая на систему человек-вагонетка и направленная горизонтально. Скорее всего это будет сила 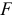 , приложенная руками человека к вагонетке, и равная силе трения
, приложенная руками человека к вагонетке, и равная силе трения
Теперь по аналогии можно сообразить, какие силы движут автомобиль. Конечно, это силы, приложенные колёсами к оси автомобиля. Колёса играют роль человека в примере с вагонеткой.
От двигателя автомобиля с помощью трансмиссии на ведущие колёса действует пара с каким-то моментом  , состоящая из двух сил.. Одна, сила
, состоящая из двух сил.. Одна, сила 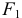 , приложена к оси, другая
, приложена к оси, другая 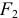 такой же величины — к дороге (рис.5.4). Эта последняя сила
такой же величины — к дороге (рис.5.4). Эта последняя сила 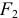 , если нет проскальзывания колёс, уравновешивается силой трения со стороны дороги. Остаётся лишь сила
, если нет проскальзывания колёс, уравновешивается силой трения со стороны дороги. Остаётся лишь сила 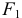 , приложенная к оси. Она и является движущей силой. И равна она, конечно, силе трения. Поэтому мы, упрощая эту схему, и говорили, что движущей силой является сила трения. На самом деле следует считать движущей силой силу
, приложенная к оси. Она и является движущей силой. И равна она, конечно, силе трения. Поэтому мы, упрощая эту схему, и говорили, что движущей силой является сила трения. На самом деле следует считать движущей силой силу 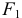 приложенную к оси автомобиля. То есть колёса, упираясь в поверхность дороги, толкают автомобиль.
приложенную к оси автомобиля. То есть колёса, упираясь в поверхность дороги, толкают автомобиль.
Работа силы трения 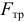 равна нулю, так как она приложена к точке касания колеса, к мгновенному центру скоростей, скорость которой равна нулю. А работу совершает сила
равна нулю, так как она приложена к точке касания колеса, к мгновенному центру скоростей, скорость которой равна нулю. А работу совершает сила 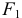 на каком-то перемещении автомобиля
на каком-то перемещении автомобиля 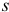 :
:
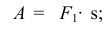
или пара:
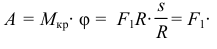
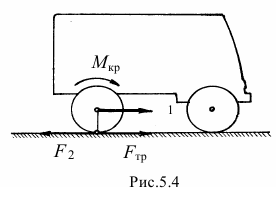
- Хорошо, Николай Степанович, тут вы меня уговорили. А объясните теперь, под действием каких сил ходит человек?
- Ну, здесь, Алёша, совсем просто. Тут никакой движущей силы нет. Человек, шагая по дороге, переносит массу своего тела с одной ноги на другую. Правда, позволяет это делать сила трения со стороны дороги. Но она не двигает человека, а лишь препятствует скольжению ног.
- Спасибо, Николай Степанович. Я вам, наверно, надоел своими глупыми вопросами?
- Да, нет. Твои, как ты говоришь «глупые» вопросы и мне порою бывают интересны. Позволяют иногда избавиться от привычных представлений о некоторых явлениях, по-другому их объяснить.
Вопрос №6 «О ВЕЛОСИПЕДЕ»
- Николай Степанович, мы с ребятами пытались понять, почему на велосипеде можно ездить, не держась за руль, «без рук». И мне кажется, что моё объяснение, которое я предложил, самое правильное
- Ну, и как же ты объяснил это движение «без рук»?
- Я не забыл ваши лекции по теории гироскопа. Ведь переднее колесо, которым управляется велосипед, очень похоже на гироскоп. У него есть ось материальной симметрии и вращается оно с большой скоростью вокруг этой оси.
Теперь вспомним, почему велосипед вообще едет и не падает. Все знают, что если он начнёт падать, то нужно руль повернуть в сторону падения и велосипед выправится. Велосипедист это делает инстинктивно и в самом начале падения. Так что эти действия и не заметны.
- Так. Всё это верно. И что же произойдёт, когда велосипедист отпустит руль?
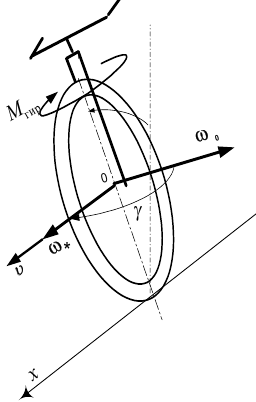
- Да всё очень просто объясняется с помощью гироскопического момента. Он возникает, когда ось гироскопа отклоняется, совершает поворот вокруг какой-то другой оси. Вот я нарисовал картинку. Правда, не весь велосипед, а только переднее колесо с рулём (см. рисунок). На этой картинке велосипед движется к нам со скоростью
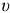 . Колесо вращается вокруг своей оси с угловой скоростью собственного вращения
. Колесо вращается вокруг своей оси с угловой скоростью собственного вращения 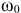 . Пусть велосипед начал отклоняться от вертикальной плоскости вправо, вращаясь вокруг горизонтальной оси
. Пусть велосипед начал отклоняться от вертикальной плоскости вправо, вращаясь вокруг горизонтальной оси 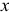 с угловой скоростью
с угловой скоростью 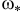 Вектор её я нарисовал в центре колеса.
Вектор её я нарисовал в центре колеса.
Гироскопический момент 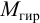 поворачивает колесо с рулём так, чтобы вектор
поворачивает колесо с рулём так, чтобы вектор 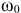 совпал с вектором
совпал с вектором 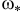 , то есть вправо, в сторону падения велосипеда. И велосипед вернётся в вертикальную плоскость.
, то есть вправо, в сторону падения велосипеда. И велосипед вернётся в вертикальную плоскость.
Что ж, Алёша, ты стал хорошо пользоваться понятиями теоретической механики. Всё правильно. Но ты хоть попробовал оценить величину этого гироскопического момента?
Попробовал. Гироскопический момент определяется формулой
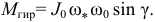
Причём у нас
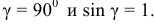
Величина гироскопического момента в основном определяется моментом инерции 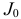 и угловой скоростью собственного вращения
и угловой скоростью собственного вращения 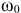 которая зависит от скорости движения велосипеда:
которая зависит от скорости движения велосипеда: 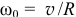 . Так что велосипед будет тем устойчивее, чем колесо массивнее и чем больше скорость движения
. Так что велосипед будет тем устойчивее, чем колесо массивнее и чем больше скорость движения 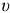 .
.
Молодец, Алёша. А как, по-твоему, можно повернуть велосипед во время движения, например, вправо, «без руля»?
Конечно можно. Надо движением туловища наклонить велосипед в правую сторону. Колесо, как мы только что выяснили, тоже повернётся вправо. И велосипед поедет туда, куда мы захотели. А чтобы удержать колесо в этом положении, нужно моментом веса человека относительно оси 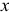 уравновесить гироскопический момент, который в этом случае, когда вектор
уравновесить гироскопический момент, который в этом случае, когда вектор 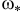 направлен вертикально вниз, располагается в плоскости, перпендикулярной оси
направлен вертикально вниз, располагается в плоскости, перпендикулярной оси 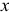 и стремится вернуть колесо в первоначальное нормальное положение.
и стремится вернуть колесо в первоначальное нормальное положение.
- Всё отлично, Алёша. Только небольшое, но важное замечание. Твоя картинка не очень точна. У велосипеда передняя вилка на самом деле расположена не вертикально — немного наклонена назад. И мало того, она не прямая, а изогнута внизу вперёд. Зачем так сделано? При твоей конструкции, посмотри на рисунок, сила трения от дороги, приложенная к колесу, направлена по оси
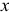 . Причём всегда, как бы мы не поворачивали колесо. Такая сила трения не может повернуть велосипед. А вот у реальной конструкции при повороте колеса эта сила трения окажется в стороне от оси
. Причём всегда, как бы мы не поворачивали колесо. Такая сила трения не может повернуть велосипед. А вот у реальной конструкции при повороте колеса эта сила трения окажется в стороне от оси 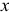 , создаст момент, пару сил, которая и поворачивает велосипед.
, создаст момент, пару сил, которая и поворачивает велосипед.
А вообще я доволен тобой. Чувствуется, что наши беседы вызвали у тебя большой интерес к теоретической механике, помогли понять законы механики и научили пользоваться ими. Появятся ещё какие идеи или вопросы, приходи.
Вопрос №7 «О ТЕОРЕМЕ ПРО КИНЕТИЧЕСКУЮ ЭНЕРГИЮ И НЕМНОГО ОБ УДАРЕ»
Николай Степанович, один преподаватель кафедры физики предложил студентам группы, в которой он вёл занятия, очень оригинальный способ, как надо действовать человеку, если он случайно или по вынужденным катастрофическим обстоятельствам начал падать с большой высоты. Чтобы скорость падения в момент встречи с землёй была меньше, надо мол перед самым падением быстро двигать, крутить-вертеть руками и ногами, извиваться всем телом, то есть значительно увеличить кинетическую энергию. По теореме об изменении кинетической энергии 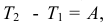 где
где 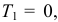 , работа
, работа 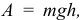 а кинетическая энергия в конце будет
а кинетическая энергия в конце будет 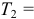
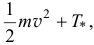 где
где 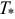 — дополнительное увеличение энергии, получаем
— дополнительное увеличение энергии, получаем
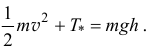
Тогда скорость падения
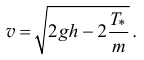
Так что, если очень постараться, можно скорость падения сделать даже равной нулю. И никакого парашюта не надо!
- И что, Алёша, всё это предлагалось вполне серьёзно?
- Не знаю. Правда, он предложил студентам сначала разобраться в этом, а потом уж «прыгать с пятого этажа».
- Слава богу … Ваш физик пошутил, конечно. А как восприняли студенты такое предложение?
- Некоторые сказали, что всё это ерунда, что такого быть не может. Но объяснить, опровергнуть не могли.
- А как ты сам, Алёша, думаешь?
- Ну, меня, старого воробья, на мякине не проведёшь. Мне кажется всё довольно просто. Не следует забывать, что надо учитывать работу не только внешних, но и внутренних сил. Чтобы двигать руками и ногами нужно совершить работу внутренними силами — силами мышц и других частей тела. Эта работа окажется в точности равной этой дополнительной энергии
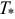 .
.
И, кроме того, Николай Степанович, теорема о движении центра масс утверждает, что внутренние силы не могут изменить движение центра масс тела, так как сумма их всегда равна нулю.
- Всё правильно. Но у этой простой, казалось бы, теоремы есть мелкие, но очень вредные «заковыки». Некоторые механики утверждают, что внутренние силы не надо учитывать при движении неизменяемой системы. А что такое «неизменяемая» система — не уточняют. Говорят, что падающий человек — неизменяемая система. Поэтому, мол, внутренние силы учитывать не надо. Но какая же она неизменяемая, эта система, руки-ноги-то меняют своё положение. Или другой пример: автомобиль — изменяемая система? Конечно. У него там много чего крутится-вертится. Так надо учитывать внутренние силы при движении таких систем? Работу внутренних сил надо учитывать, если, конечно, она совершается. А сумму внутренних сил — нет. Главный вектор и главный момент их будут равны нулю. Хотя они, как ты знаешь, могут и не уравновешиваться, так как приложены к разным точкам и могут изменять форму системы.
Неизменяемой является лишь система, состоящая из неизменяемых, абсолютно твёрдых тел, соединённых друг с другом недеформируемыми связями (в том числе и нерастяжимыми нитями) так, что расстояние между телами не меняется.
- Я это всё знаю, Николай Степанович. На лекции вы об этом говорили. А нет ли у вас интересной задачки, с какой-нибудь «заковыкой»?
- Что ж, вот тебе задачка, которую обычно решают на практических занятиях. Но только не всегда обращают внимание на некоторые подробности и частности. А они не так уж и скучны, и просты.
Вот я рисую диск, который стоит на краю горизонтальной плоскости и начинает скатываться без скольжения по наклонной плоскости. Нарисуй поточнее траекторию движения центра масс и найди его скорость в момент, когда диск начнёт качение по нижней, горизонтальной плоскости. А я пока схожу в деканат, там скоро начнётся небольшое совещание.
- Ну, что у тебя, Алёша, получилось? Смотрю твой рисунок. Так, начало правильное. Диск сначала вращается вокруг верхнего угла, траектория центра — дуга. Потом диск катится вниз, траектория — прямая линия. А какая картинка получается в нижнем углу?
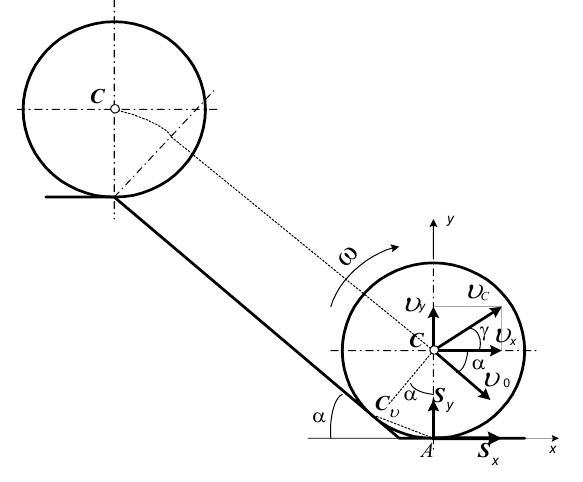
А вот эта картинка, Николай Степанович, для меня не очень ясна. Мне, кажется, тут произойдёт удар диска о горизонтальную плоскость в точке 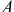 . Вектор скорости центра
. Вектор скорости центра 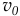 в начале удара был параллелен наклонной плоскости. Потом мгновенно становится горизонтальным. А чему становится равной эта скорость, сразу и не соображу.
в начале удара был параллелен наклонной плоскости. Потом мгновенно становится горизонтальным. А чему становится равной эта скорость, сразу и не соображу.
Давай вместе разберёмся. Явление удара исследуется с помощью двух теорем: теоремы об изменении количества движения
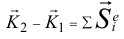
и теоремы о моменте количества движения
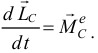
В проекциях на оси 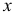 и
и 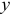 получим уравнения:
получим уравнения:
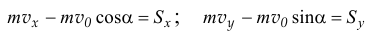
и
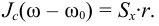
Где 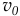 — скорость центра масс диска в начале удара с соответствующей угловой скоростью
— скорость центра масс диска в начале удара с соответствующей угловой скоростью 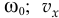 и
и  — проекции скорости центра масс на оси в конце удара при угловой скорости
— проекции скорости центра масс на оси в конце удара при угловой скорости 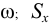 и
и 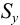 — проекции импульса ударной силы в точке
— проекции импульса ударной силы в точке 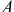 .
.
После преобразований получим три уравнения
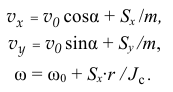
Определим ещё скорость точки 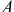 ,точки контакта диска с горизонтальной плоскостью в конце удара, проекции которой
,точки контакта диска с горизонтальной плоскостью в конце удара, проекции которой
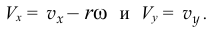
Нам не хватает двух уравнений, которые должны характеризовать результат удара, физические свойства поверхности и тела. Будем считать, что скольжение отсутствует. Тогда 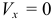 и, значит,
и, значит, 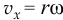 .
.
Затем положим, как это обычно предполагается при исследовании удара, что скорость отскока после удара пропорциональна скорости в начале удара:

Коэффициент 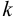 — называется коэффициентом восстановления скорости. Определяется он опытным путём. Так как
— называется коэффициентом восстановления скорости. Определяется он опытным путём. Так как
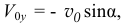
то
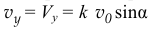
(см. рисунок).
Итак, имеем пять уравнений с пятью неизвестными, и все они теперь могут быть определены. Так, для диска, момент инерции которого 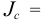
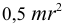 , легко находим проекции скорости центра масс на оси
, легко находим проекции скорости центра масс на оси
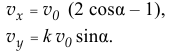
Значит, диск подскакивает над плоскостью под углом 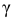 таким, что тангенс его
таким, что тангенс его
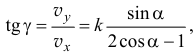
и диск будет вращаться с угловой скорость
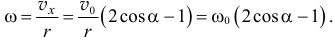
Если упругость поверхности равна нулю 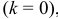 , то скорость центра
, то скорость центра 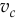 будет направлена параллельно плоскости, горизонтально
будет направлена параллельно плоскости, горизонтально 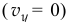 и равна
и равна
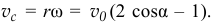
Интересно, что при  скорость
скорость 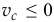 , что невозможно. Значит, диск остановится. Вся энергия уйдёт на деформацию поверхности.
, что невозможно. Значит, диск остановится. Вся энергия уйдёт на деформацию поверхности.
И ещё один важный вывод. Чтобы не произошло такого удара и всех этих нежелательных явлений, переход от наклонной плоскости к горизонтальной должен быть плавным, по кривой, радиус кривизны которой должен быть больше радиуса диска.
- Спасибо, Николай Степанович, за интересную задачу. А вот с явлением удара мне надо познакомиться подробнее. До свидания.
Вопрос №8 «КОЕ-ЧТО О СКАЛЯРНОМ ПРОИЗВЕДЕНИИ»
- Ну и любопытный же ты, Алёша … Откуда ты об этом узнал?
- Я подслушал, как у вас на кафедре об этом говорили. Не то возмущались, не то удивлялись. А толком не понял, о чём шёл разговор.
- Что ж, если тебе интересно, я сейчас расскажу. Тем более это тебе будет полезно. Ведь ты после института всерьёз хочешь заняться теоретической механикой. Разговор шёл о принципе возможных перемещений и, в частности, об этом возможном, или по-другому виртуальном перемещении. Ты знаешь, что это такое, объяснять не буду. Мы спорили о том, как его изображать — вектором или малым отрезком касательной к траектории возможного движения точки. Большинство учёных представляют его в виде вектора, малого приращения радиуса-вектора точки —
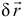 . И в результате из-за этого иногда получают странный и неверный вывод. Началом разговора на кафедре послужила цитата из одного солидного учебника, автор которого считался большим авторитетом ещё сто лет тому назад [8, с.303].
. И в результате из-за этого иногда получают странный и неверный вывод. Началом разговора на кафедре послужила цитата из одного солидного учебника, автор которого считался большим авторитетом ещё сто лет тому назад [8, с.303].
Короче. Он написал буквально следующее. « … Для любого виртуального перемещения сумма элементарных работ реакций идеальных связей равна нулю:
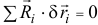
при этом для поступательного перемещения множитель 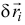 один и тот же для всех частиц, и потому он может быть вынесен за знак суммы, т.е. мы имеем
один и тот же для всех частиц, и потому он может быть вынесен за знак суммы, т.е. мы имеем
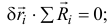
отсюда ввиду произвольности 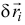 находим:
находим:
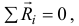
что мы и хотели доказать».
Так он хотел доказать, что при поступательном движении тела векторная сумма реакций идеальных связей равна нулю.
Даже простой пример показывает, что это не так. Действительно, при некотором поступательном скольжении твёрдого тела по гладкой плоскости реакциями являются перпендикулярные плоскости силы и сумма их, конечно, не равна нулю.
При доказательстве им допущена грубая ошибка. Ведь скалярное произведение двух векторов может быть равно нулю не только тогда, когда равен нулю один из них, но и тогда, когда они перпендикулярны друг другу. Если бы он записал условие идеальности реакций в алгебраическом виде, то получилось бы так:

Отсюда следует, что это условие будет выполняться не только при 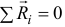 , но и при
, но и при 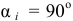 или
или 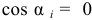 , то есть, если возможные перемещения перпендикулярны силам. Как это и получилось в моём примере.
, то есть, если возможные перемещения перпендикулярны силам. Как это и получилось в моём примере.
- Ого, Николай Степанович, мне кажется, что даже я не сделал бы такой элементарной ошибки.
- Надеюсь. Получается так, что чем умнее и опытнее учёные мужи, тем больше у них небрежности в рассуждениях. Аналогичные ошибки мы обнаружили и в других, более современных учебниках.
Вот сам посуди. При свободном движении тела возможные перемещения точек есть результат суммы двух перемещений (см. рисунок): перемещения 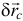 . какого-либо полюса
. какого-либо полюса 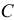 и поворота точек вокруг этого полюса, перемещения
и поворота точек вокруг этого полюса, перемещения 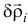 :
:
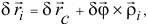
где 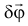 вектор бесконечно малого поворота тела. Тогда по принципу возможных перемещений при равновесии тела
вектор бесконечно малого поворота тела. Тогда по принципу возможных перемещений при равновесии тела
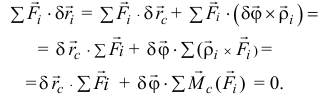
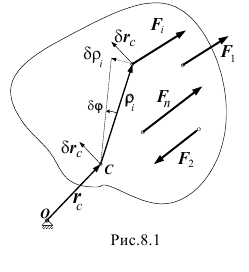
Далее авторы рассуждают так [3,5]. «В силу произвольности векторов 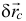 и
и 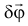 получим:
получим:

То есть получаем известные условия равенства нулю главного вектора и главного момента сил, условия равновесия тела».
Но, а если эти силы, действующие на тело, параллельны и перемещения 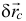 окажутся перпендикулярными им, да ещё и вектор
окажутся перпендикулярными им, да ещё и вектор 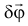 назначим параллельным этим силам, то эти условия будут удовлетворяться и для не-уравновешивающихся сил. Вот таков ляпсус получается, когда забываем, как определяется скалярное произведение векторов, что они могут оказаться перпендикулярными друг другу.
назначим параллельным этим силам, то эти условия будут удовлетворяться и для не-уравновешивающихся сил. Вот таков ляпсус получается, когда забываем, как определяется скалярное произведение векторов, что они могут оказаться перпендикулярными друг другу.
Поэтому я и стараюсь, Алёша, возможные перемещения не представлять вектором. В этом нет особой необходимости и это будет проще и надёжнее.
И ещё одно замечание. Вот когда ты станешь лектором … Не смейся, я надеюсь на это. Зачем же мы тогда столько копаемся в теоретической механике? Вот когда ты станешь лектором, преподавателем, то, формулируя принцип возможных перемещений, не говори «сумма работ сил на любом возможном перемещении», а говори — на всяком возможном перемещении. Чтобы хотя бы одно из них не оказалось перпендикулярным силам. Всё понял? Ну и хорошо.
Вопрос №9 «PERPETUUM MOBILE»
- Николай Степанович, зачем вы направили ко мне этого изобретателя? Он же придумал «вечный двигатель»! Я сначала пытался убедить его, что таких двигателей не существует и быть не может. Но он был так настойчив, что мне пришлось посмотреть его проект. И сразу обнаружилась его элементарная безграмотность в механике и физике. Он даже правило рычага не знает. Да и школьная математика у него хромает. В общем, он стал ругаться, обзывать меня по-всякому… и я прогнал его.
- Ох, Алёша, извини меня … Я специально его к тебе направил, чтобы потом поговорить об этих «вечных двигателях».
Мне самому не раз приходилось разговаривать с такими изобретателями. И убедить их в бесплодности попыток построить такую конструкцию невозможно. Даже встречал таких изобретателей, которые и изучали когда-то механику, знают её законы, в том числе и закон сохранения энергии. Доказать им это практически очень трудно, так как конструкции порой такие заковыристые, что математические исследования движения этих систем, как правило, очень сложны.
Ранее были такие доморощенные изобретатели, которые всю жизнь посвящали совершенствованию своего детища. Первые конструкции «вечного двигателя» появлялись ещё в XIII веке. И, чтобы избавиться от назойливости этих изобретателей, в 1775 году французская академия сделала официальное заявление, что никакие проекты вечных двигателей к рассмотрению и испытаниям больше не принимаются.
Несмотря на это до сих пор такие проекты поступают. Ты сам в этом только что убедился. А вот на рис. 9.1 проект «вечного двигателя» ещё XIII века. Ты сможешь понять принцип его действия? Грузы на стержнях перекидываются на шарнирах и давят на упоры, прикреплённые к колесу. По мысли автора, колесо будет само всё время, вращаться по часовой стрелке.
На первый взгляд он прав, так как сумма моментов правых грузов весом 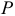 относительно оси вращения
относительно оси вращения
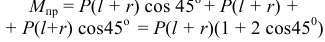
больше суммы моментов левых
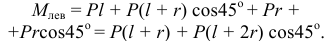
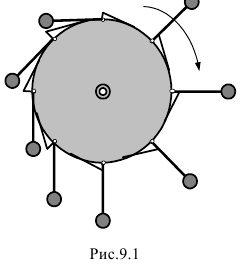
Разность их легко подсчитать
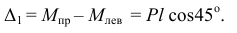
И когда колесо сделает четверть оборота, все стержни с грузами повернутся, картинка опять станет прежней и новые грузы заставят колесо сделать следующую четверть оборота и так далее. И чем больше длина стержней 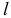 , считает автор, тем больше будет эта разность
, считает автор, тем больше будет эта разность  и тем быстрее колесо будет вращаться.
и тем быстрее колесо будет вращаться.
- Но, Николай Степанович, даже из этой картинки видно, что когда колесо повернётся на 45°, момент сил тяжести левых грузов, наверное, станет больше момента правых! И он затормозит вращение колеса.
- Да, ты прав. Момент левых будет больше момента правых на величину
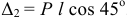 . В конце концов, учитывая ещё и трение в подшипниках оси, колесо остановится, сделав по инерции несколько оборотов. Так что, конечно, этот «вечный двигатель» работать не будет.
. В конце концов, учитывая ещё и трение в подшипниках оси, колесо остановится, сделав по инерции несколько оборотов. Так что, конечно, этот «вечный двигатель» работать не будет.
Но неожиданно через шестьсот с лишним лет в 1910 году нашёлся новый изобретатель похожего колеса. Даже известно имя автора, которым и называется его изобретение — колесо Орфиреуса. Он рассуждал так. Во-первых, надо сделать длиннее стержни и тогда  будет значительно больше, торможение станет меньше. И, во-вторых, надо сделать не восемь стержней, а как можно больше. Стержни будут беспрерывно перекидываться и торможения, мол, практически не будет.
будет значительно больше, торможение станет меньше. И, во-вторых, надо сделать не восемь стержней, а как можно больше. Стержни будут беспрерывно перекидываться и торможения, мол, практически не будет.
Хороша его идея? Но научное учреждение, куда он направил свой проект, отвергло его, даже не рассмотрев. И правильно сделало. Но я всё же попробовал провести небольшой анализ, чтобы убедить сторонников Орфериуса, что его конструкция работать не будет.
Вот это колесо (рис. 9.2). Я, правда, нарисовал не очень много этих грузиков, всего 24, но определенные выводы можно всё-таки сделать.
Тебе понятна его конструкция? Я сначала предположил, что колесо вращается по часовой стрелке (рис. 9.2). Тогда грузики расположатся так, как показано на рисунке.
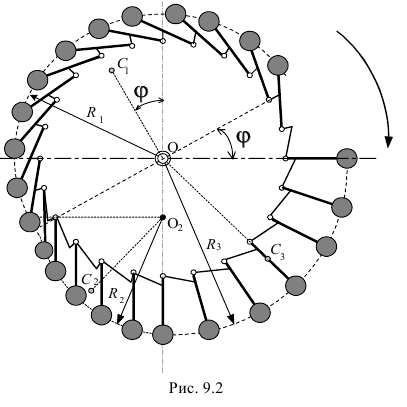
Из рисунка видно, что расположение грузиков можно разбить на три области: первая — состоящая из грузиков, откинутых на косые стороны упоров и расположенных на полуокружности радиусом 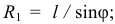 вторая — из вертикально висящих грузиков, расположенных на четверти окружности радиусом
вторая — из вертикально висящих грузиков, расположенных на четверти окружности радиусом 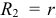 равном радиусу самого колеса с центром
равном радиусу самого колеса с центром 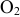 , смещённым вниз на длину стержней
, смещённым вниз на длину стержней 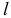 . И третья область — занимающая тоже четверть окружности, окружности радиусом
. И третья область — занимающая тоже четверть окружности, окружности радиусом 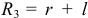 , образованной грузиками, стержни которых опираются на прямые стороны упоров.
, образованной грузиками, стержни которых опираются на прямые стороны упоров.
Центр тяжести грузиков в каждой области можно найти как центр тяжести соответствующих дуг окружностей (полагая, что грузики располагаются по ней равномерно) по известной формуле
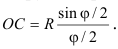
Так, центр 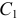 первой области находится на расстоянии
первой области находится на расстоянии 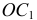 по оси симметрии дуги, равном
по оси симметрии дуги, равном
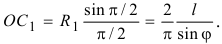
Центр тяжести  грузиков во второй области — на расстоянии
грузиков во второй области — на расстоянии 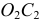 , расположенном под углом 45°, равном
, расположенном под углом 45°, равном
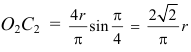
Центр тяжести грузиков в третьей области находится аналогично:
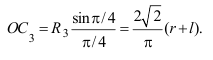
Теперь можно определить момент сил тяжести грузиков относительно оси вращения
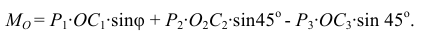
Учитывая количество грузиков в каждой области, получим:
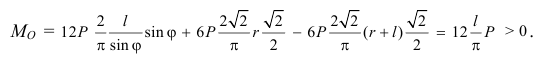
То есть на самом деле при таком расположении грузиков они будут вращать колесо не по часовой, а против часовой стрелки. И располагаться будут тогда так, как показано на рис. 9.3. Но при таком расположении грузиков даже без математических расчётов ясно, что вращение будет происходить по часовой стрелке.
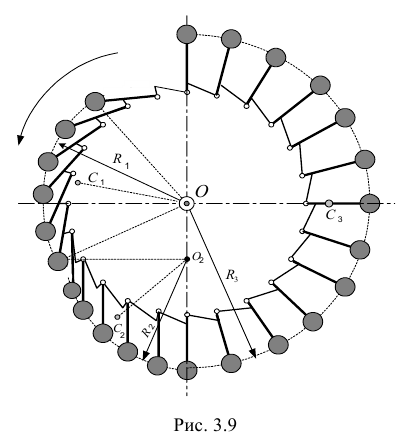
При такой неопределённости направления вращения естественно предположить, что существует положение равновесия, в котором колесо при наличии трения в подшипниках оси в конце концов остановится и успокоится.
Я, Алёша, специально направил нынешнего изобретателя к тебе, чтобы обратить твоё внимание на эти «вечные двигатели». Чтобы ты сразу, с порога, отвергал их и не тратил силы на доказательства.
Кстати, ещё недавно, в феврале нынешнего (!) года, я увидел по центральному телевидению нового изобретателя «вечного двигателя». Какой-то токарь построил у себя в гараже электродвигатель, который работает от силового поля постоянного магнита. И КПД двигателя якобы больше единицы — 1,2! Мало того, какие-то профессора пытаются и не могут объяснить это явление! Так что материал и выводы из нашей беседы, Алёша, до сих пор актуальны.
Вопрос №10 «ПРО МАССУ, КОТОРАЯ ИЗМЕНЯЕТСЯ»
- Помнишь, Алёша, как-то мы с тобой говорили о работе силы, точка приложения которой перемещается по движущемуся телу. И ты в качестве примера определял движение тяжёлой нити с помощью теоремы об изменении кинетической энергии (см. рис. 4.3). А я тогда забраковал твоё решение, так как масса нити изменяется и теорему в обычном виде применять нельзя.
- Да, я помню. И сегодня вы хотите растолковать мне, как определяется движение тел переменной массы? Это, наверно, не так просто.
- Но и не очень сложно. Всю теорию я рассказывать не собираюсь. Познакомлю только с выводами, методами решения задач.
Впервые основной закон динамики точки переменной массы был открыт профессором Петербургского политехнического института И.В. Мещерским ещё в 1897 году [3, 4, 5]. Идея его сводится к тому, что при исследовании движения тела, к которому непрерывно прибавляются или от которого отделяются частицы, материальные точки, надо учитывать кроме обычных сил ещё и дополнительные реактивные силы 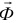 , зависящие как от массы этих частиц
, зависящие как от массы этих частиц 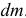 , так и от скорости их
, так и от скорости их 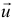 .
.
Для точки переменной массы 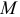 основное уравнение динамики записывается так:
основное уравнение динамики записывается так:
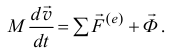
Реактивная сила
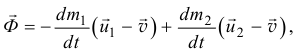
где 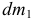 и
и 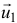 — масса и абсолютная скорость отделяемых частиц, а
— масса и абсолютная скорость отделяемых частиц, а 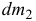 и
и 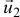 — соответственно масса и скорость присоединяемых частиц,
— соответственно масса и скорость присоединяемых частиц, 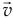 — скорость самой точки.
— скорость самой точки.
Основные теоремы для тела переменной массы по форме похожи на соответствующие теоремы для тела постоянной массы. Надо только иметь в виду, что центр масс перемещается по телу. Поэтому, например, количество движения определяется также, как для тела постоянной массы:
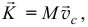
только здесь 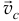 — скорость той точки тела, с которой совпадает центр масс в данный момент.
— скорость той точки тела, с которой совпадает центр масс в данный момент.
- Николай Степанович, ведь мы как раз говорили об этом в одной «беседе», когда докладывали на кафедре о работе силы, точка приложения которой перемещается по телу!
- Да-да, правильно. Ну, а теорема об изменении количества движения тела переменной массы после несложных математических преобразований запишется так, в дифференциальном виде:
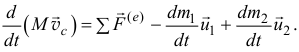
В частности, для системы переменной массы, у которой частицы либо только отделяются, или только присоединяются (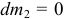 или
или 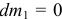 ) это уравнение соответственно становится проще. Интересен и случай, когда абсолютные скорости тех и других частиц равны нулю — уравнение становится совсем удобным, похожим на теорему об изменении количества движения тела постоянной массы
) это уравнение соответственно становится проще. Интересен и случай, когда абсолютные скорости тех и других частиц равны нулю — уравнение становится совсем удобным, похожим на теорему об изменении количества движения тела постоянной массы
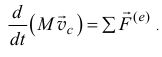
Полезна при решении задач и теорема об изменении кинетической энергии тела переменной массы. Например, для тела, от которого лишь отделяются частицы, теорема записывается так (при 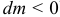 ):
):
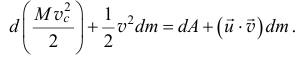
А если частицы отделяются с абсолютной скоростью, равной нулю, 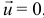 , или
, или 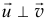 , то совсем просто:
, то совсем просто:
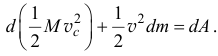
То есть от кинетической энергии тела вычитается кинетическая энергия отделяющихся частиц (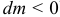 ).
).
- Николай Степанович, вы говорили, что всё очень просто. А мне кажется — совсем не просто. Ведь для тела постоянной массы теорема выглядит удобнее, записывается в проинтегрированном виде. Там оставалось только подставить значения кинетической энергии в двух положениях и вычислить работу сил. А тут, наверное, придётся решать дифференциальное уравнение и совсем не простое.
- Ты прав, конечно. Но математики дифференциальные уравнения умеют решать разными способами. Так что это трудности не механики, а математики.
Вернёмся к твоей задаче: движение по вертикали одного конца нити при закреплённом втором (см. рис.4.3). Помнишь эту задачу? Там как раз скорость отделяемых частиц 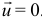 . Поэтому воспользуемся уравнением (10.5).
. Поэтому воспользуемся уравнением (10.5).
Масса движущейся части нити
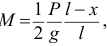
масса отделяемых частиц
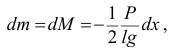
элементарная работа
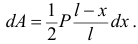
(Я использую результаты твоего прошлого решения, они тут будут такими же). Причем,
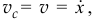
так как эта часть нити движется поступательно.
Находим дифференциал кинетической энергии тела
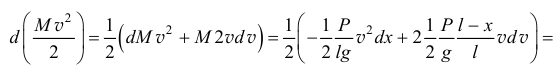
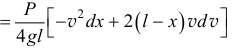
и подставляем в уравнение (10.5):

Поделив на  , после математических преобразований получим дифференциальное уравнение
, после математических преобразований получим дифференциальное уравнение
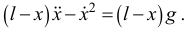
Положив в нем
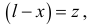
уравнение запишем так:
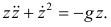
Решение этого нелинейного уравнения, поверь мне:
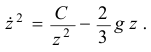
Так как при
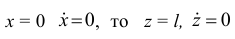
и постоянная
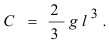
Значит,

и скорость конца нити после подстановки
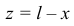
будет такой:
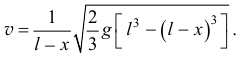
Если сравнить с результатом твоего прошлого неправильного решения, то можно заметить, что при одинаковой качественной зависимости 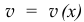 значения скорости получаются несколько большими. Так, при
значения скорости получаются несколько большими. Так, при 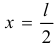 у тебя
у тебя 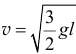 , а у меня здесь
, а у меня здесь 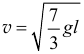 . Это естественно, потому что при той же работе силы тяжести кинетическая энергия тела получается меньше.
. Это естественно, потому что при той же работе силы тяжести кинетическая энергия тела получается меньше.
И ещё. Так как теорема эта используется в дифференциальном виде, то для исследования движения аналогичных систем иногда выгоднее использовать теорему об изменении количества движения, которая для тела с отделяющимися частицами записывается так:
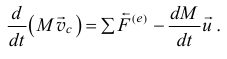
А для некоторых частных случаев получается ещё проще. Так, если абсолютная скорость отделяемых частиц 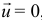 , уравнение становится таким:
, уравнение становится таким:
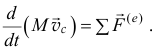
То есть по форме напоминает теорему для тела постоянной массы. А если относительная скорость равна нулю 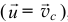 , то ещё проще
, то ещё проще
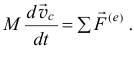
В этом случае срабатывает и закон сохранения количества движения: при
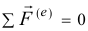
получается
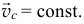
Только что рассмотренную задачу можно решить проще с помощью этой теоремы (10.8), так как абсолютная скорость 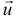 отделяемых частиц равна нулю
отделяемых частиц равна нулю
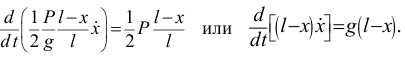
Вычислив производные, получим то же уравнение, что и ранее:
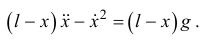
На сегодня, Алёша, хватит. Я сообщил довольно много сложного материала. Тебе надо его освоить, так сказать, переварить. Попробуй дома решить вот такую непростую задачу. Я понимаю, тебе сейчас не до этого -экзаменационная сессия скоро, зачётов много. И я тебя не тороплю. Когда сможешь, приходи. Не получится, тоже приходи.
Задача Николая Степановича

Рулон однородной тяжёлой ленты скатывается по наклонной плоскости. При этом лента, прикреплённая свободным концом В к плоскости, разматывается. Определить скорость центра рулона как функцию длины смотанной нити 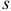 . Полная длина нити —
. Полная длина нити — 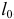 , толщина нити —
, толщина нити — 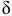 .
.
(Задача оказалась сложной. Алёша не сумел её решить. Поэтому даём решение, сделанное самим автором этой задачи, Николаем Степановичем.)
Воспользуемся теоремой об изменении кинетической энергии в форме (10.5), так как абсолютные скорости отделяемых от рулона частей ленты равны нулю
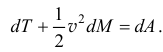
Если радиус скатывающегося рулона — 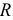 , то длина ленты на рулоне (как площадь рулона, делённая на толщину ленты)
, то длина ленты на рулоне (как площадь рулона, делённая на толщину ленты)
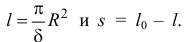
Масса рулона
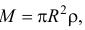
где 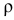 — масса единицы площади рулона. Или
— масса единицы площади рулона. Или
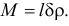
Масса отделяющихся частей
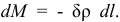
Кинетическая энергия рулона, как цилиндра при плоскопараллельном движении,

Так как
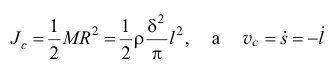
и

Элементарная работа сила тяжести рулона
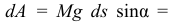
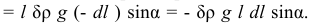
Определяем дифференциал кинетической энергии
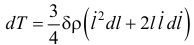
и составляем уравнение
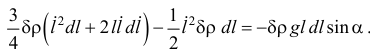
Поделив на 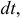 получим
получим
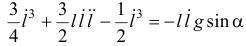
или
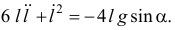
Это нелинейное дифференциальное уравнение. Попробуем найти его решение. Тем более, что уравнения такого вида обычно получаются при исследовании тел переменной массы.
Обозначим
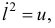
тогда
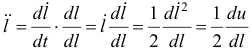
и уравнение (10.10) можно привести к виду
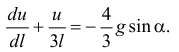
Представим переменную 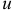 как произведение двух функций
как произведение двух функций
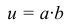
Тогда 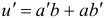 (штрихом обозначена производная по
(штрихом обозначена производная по  ). Подставим в уравнение (10.11):
). Подставим в уравнение (10.11):
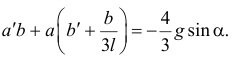
Одну из переменных 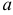 и
и 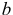 можно выбрать произвольно. Положим
можно выбрать произвольно. Положим
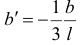
или
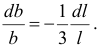
Отсюда
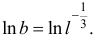
Значит
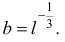
Подставив результаты в (10.13), получим
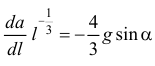
или
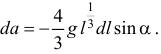
Проинтегрировать, найдем
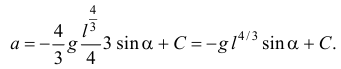
Поэтому функция 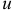 , по (10.12),
, по (10.12),
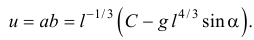
В начале движения
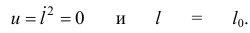
Значит
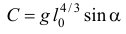
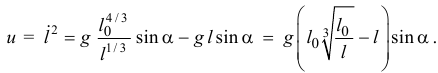
И так как
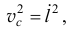
а
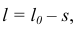
то окончательно
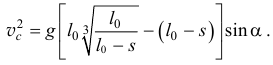
Так как с течением времени длина ленты в рулоне 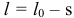 уменьшается, то скорость центра рулона
уменьшается, то скорость центра рулона 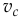 увеличивается. И в конце движения, когда вся лента смотается, при
увеличивается. И в конце движения, когда вся лента смотается, при  , скорость конца ленты станет равной бесконечности.
, скорость конца ленты станет равной бесконечности.
Николай Степанович предложил решение ещё одной очень интересной задачи, в которой также определяется движение тела переменной массы. Вот эта задача (рис. 10.2).
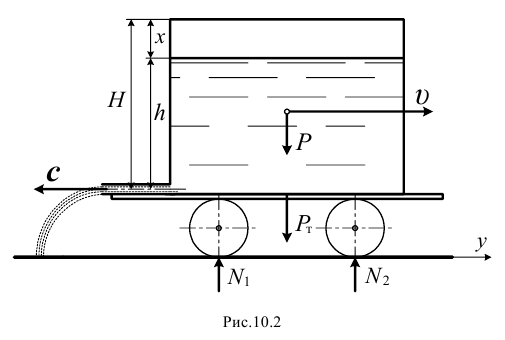
На тележке установлен бак, доверху заполненный жидкостью. В некоторый момент жидкость стала вытекать из горизонтальной сливной трубы.
И под действием реактивной силы тележка начала движение. Определим её движение, предполагая, что уровень жидкости всё время остаётся горизонтальным. Сопротивления движению учитывать не будем.
На примере решения этой задачи ещё раз продемонстрируем методику исследования движения тел переменной массы. Воспользуемся уравнением Мещерского (10.1), которое запишем так:
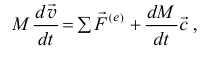
где 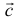 — относительная скорость вытекающей жидкости.
— относительная скорость вытекающей жидкости.
Проектируя уравнение на горизонтальную ось (рис. 10.2), получим:
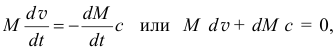
где 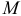 — масса тяжести с баком.
— масса тяжести с баком.
Она равна
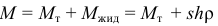
(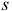 — площадь бака,
— площадь бака,  — высота уровня жидкости,
— высота уровня жидкости,  — плотность жидкости). Масса отделяющих частиц
— плотность жидкости). Масса отделяющих частиц 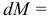
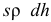 . Так как скорость вытекающей жидкости по формуле Торичелли
. Так как скорость вытекающей жидкости по формуле Торичелли
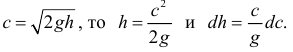
Дифференциальное уравнение движения получится так:
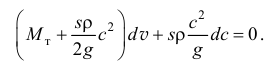
Обозначим
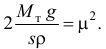
После несложных преобразований получим уравнение
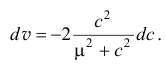
Решение его известно (это табличный интеграл):
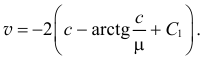
Так как в начале движения при
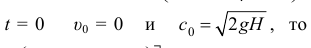
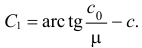
Значит
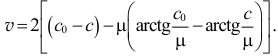
И при
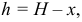
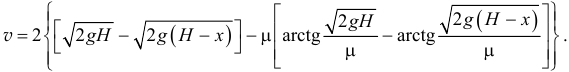
Наконец, по закону непрерывности струи протекающей жидкости за единицу времени, имеем равенство
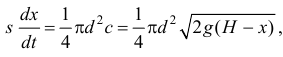
где 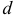 — диаметр сливной трубы.
— диаметр сливной трубы.
Обозначим для удобства
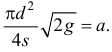
Тогда
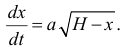
Разделив переменные и проинтегрировав, получим
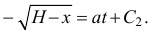
и так как при
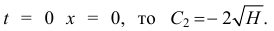
Поэтому
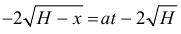
или
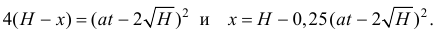
Подставив это значение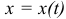 в (10.17), получим зависимость скорости тележки от времени. График скорости
в (10.17), получим зависимость скорости тележки от времени. График скорости 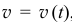 похожий на параболу, имеет вид, показанный на рис. 10.3.
похожий на параболу, имеет вид, показанный на рис. 10.3.
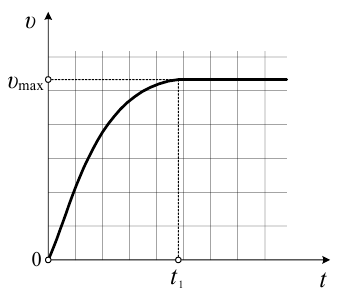
В момент
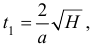
когда выльется вся жидкость, скорость станет максимальной, постоянной и равной
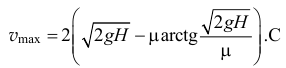
Стоит заметить, что эта скорость не зависит от диаметра сливной трубы. Например, при
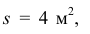
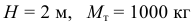
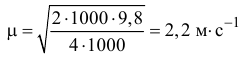
Вопрос №11«ПРО РАСПРЕДЕЛЁННЫЕ СИЛЫ»
- Слушай, Алексей….У тебя же каникулы начались, езжай домой. Отдыхать надо. А ты опять ко мне с какими-то вопросами. Ну, ладно, что тебя интересует, что тебе не нравится?
- Да, у меня, Николай Степанович, совсем маленький вопросик. Это о распределённой нагрузке. В учебниках по теоретической механике, да и в ваших лекциях, рассматривалась нагрузка распределённая только по прямой линии. Да и располагалась эта линия либо горизонтально, либо вертикально. И ни одной задачки не было, в которой нагрузка приложена к наклонной прямой и тем более к кривой линии.
- Ты считаешь, что надо о распределённых силах поговорить подробнее? Может ты и прав. Действительно, мы рассматриваем только простейшие случаи. Хотя, Алёша, есть учебники и задачники, в которых можно найти примеры нагрузки распределённой и по наклонной прямой линии и сделаны замечания о решении задач с неравномерно распределёнными силами и не только по прямой линии. Кстати, и я на лекции говорил о силе, распределённой по дуге окружности.
- Я помню, Николай Степанович. Но ваш пример довольно примитивен, прост.
- Ишь-ты, уж начал критиковать и учителя своего! Ладно, не сержусь. Ты прав. Пойдём на кафедру, я покажу подготовленную недавно статейку как раз на эту тему. Ты словно предугадал её появление. Опубликовать её я ещё не успел. Так что ты первый, кому её показываю. Вот рукопись этой статьи. Но я статью тебе не дам, просто расскажу её содержание.
- Вот смотри… Распределённую нагрузку, действующую на точки тела, я бы разделил на два класса. Во-первых, на собственные силы ,силы принадлежащие самим точкам, которые не зависят от того, как деформировано тело и как оно расположено. Такие силы называют ещё объёмными, или массовыми силами, то есть действующими на единицу объёма или массы. Подобные силы появляются, когда тело находится в однородном силовом поле. Например, сила тяжести тела, вес, это распределённые силы, распределённые по всем его точкам. Мало того, они всегда направлены вертикально и равнодействующая их, вес всего тела, сосредоточенная сила, приложенная к центру тяжести и равная сумме этих параллельных сил.
К таким силам можно отнести также и силы электрического или магнитного полей.
Интенсивность 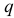 таких собственных сил, например, сил тяжести, определяется как сила, равная весу единицы объёма, площади или, если тело -линия (рис.11.1), единицы длины. А размерность интенсивности равна размерности силы, делённой на размерность площади, объёма или длины.
таких собственных сил, например, сил тяжести, определяется как сила, равная весу единицы объёма, площади или, если тело -линия (рис.11.1), единицы длины. А размерность интенсивности равна размерности силы, делённой на размерность площади, объёма или длины.
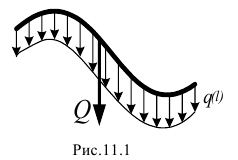
Конечно, интенсивность 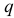 может быть не постоянной, не равномерно распределённой по длине, если эта линия не однородна по массе. И тогда равнодействующая их, вес всей линии будет сосредоточенной силой и может быть определена как криволинейный интеграл:
может быть не постоянной, не равномерно распределённой по длине, если эта линия не однородна по массе. И тогда равнодействующая их, вес всей линии будет сосредоточенной силой и может быть определена как криволинейный интеграл:
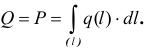
А точка приложения или линия действия равнодействующей находятся по правилам определения центра тяжести с помощью теоремы Вариньона.
Второй класс — силы также распределённые, но действующие на данное тело со стороны другого тела или со стороны среды, в которой данное тело находится, например, при действии жидкости или газа (воды, ветра и т.п.). Такими силами является и вес частиц какого-то тяжелого материала, насыпанного на тело. Подобную нагрузку называют ещё поверхностными силами.
На рис.11.2 показана неравномерно распределённая поверхностная нагрузка, действующая на наклонную прямую, например, действие веса снега на часть крыши дома. (Здесь и в дальнейшем мы будем представлять линию в виде ленты, имеющей ширину. То есть она практически больше похожа на узкую поверхность).
Заметим, что эти параллельные силы интенсивности 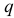 можно условно перенести по линиям действия на горизонтальную прямую, на ось
можно условно перенести по линиям действия на горизонтальную прямую, на ось 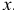 . Но тогда интенсивность будет определяться другой закономерностью
. Но тогда интенсивность будет определяться другой закономерностью
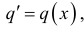
а величина равнодействующей
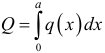
останется прежней так же, как и линия действия ее.
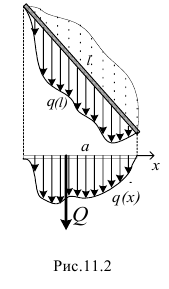
Нередко эти поверхностные силы интенсивности 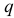 оказываются перпендикулярными прямой линии, а при действии на кривую линию, направленными по нормалям к ней, если считать эти линии гладкими, не учитывать трение и какие-то другие препятствия, ограничивающие скольжение нагрузки. К таким нагрузкам относится, например, давление жидкости или газа как в состоянии покоя, так и при движении.
оказываются перпендикулярными прямой линии, а при действии на кривую линию, направленными по нормалям к ней, если считать эти линии гладкими, не учитывать трение и какие-то другие препятствия, ограничивающие скольжение нагрузки. К таким нагрузкам относится, например, давление жидкости или газа как в состоянии покоя, так и при движении.
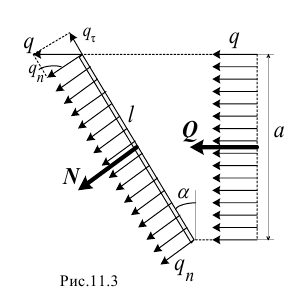
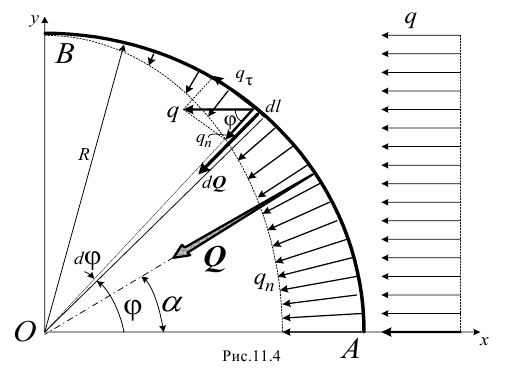
Вспомни, Алёша, физику, где доказывалось, что давление идеальной невязкой жидкости всегда направлено по нормалям к поверхности тела.
Действительно (рис. 11.3). если разложить силу интенсивности  на две составляющие по нормали к линии
на две составляющие по нормали к линии 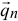 и по касательной к ней
и по касательной к ней 
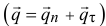 , то при отсутствии трения должна быть равной нулю
, то при отсутствии трения должна быть равной нулю  , и останется тогда только нормальная составляющая
, и останется тогда только нормальная составляющая 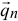 . Если линия прямая, расположенная под углом
. Если линия прямая, расположенная под углом 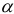 к вертикали, то действие среды на прямую будет определяться лишь нормальной интенсивностью
к вертикали, то действие среды на прямую будет определяться лишь нормальной интенсивностью

И равнодействующая интенсивности будет равна
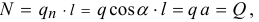
то есть равна равнодействующей сил, приложенных к линии со стороны среды.
На рис.11.4 рассмотрен более сложный пример. Показано действие движущегося потока жидкости интенсивности 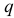 на дугу, равную четверти окружности радиусом
на дугу, равную четверти окружности радиусом 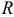 .
.
Если каждую силу интенсивности  разложить на составляющие, касательную
разложить на составляющие, касательную  и нормальную
и нормальную 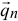 и учесть только нормальную составляющую, направленную по радиусу дуги, получится распределённая неравномерная нагрузка интенсивности
и учесть только нормальную составляющую, направленную по радиусу дуги, получится распределённая неравномерная нагрузка интенсивности
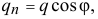
где 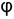 — угол, определяющий точку приложения данной силы
— угол, определяющий точку приложения данной силы 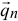 .
.
Сила, действующая в данном месте на участок длиной  , элементарная сила
, элементарная сила
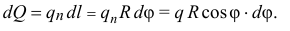
Проекция на ось 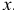 равнодействующей всей нагрузки
равнодействующей всей нагрузки
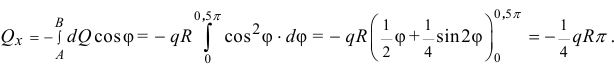
Проекция на ось 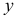
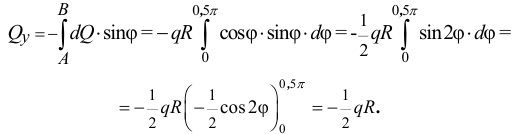
Величина всей равнодействующей нагрузки на дугу
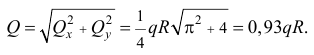
Вектор равнодействующей сходящихся сил 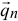 направлен по радиусу дуги к центру
направлен по радиусу дуги к центру 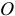 под углом
под углом 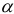 , тангенс которого
, тангенс которого
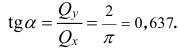
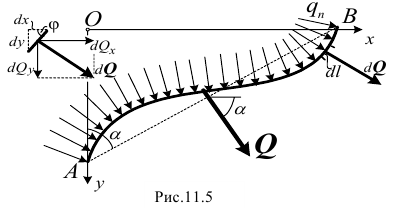
И угол

Интересную и полезную зависимость обнаружил С.Тимошенко («Инженерная механика», 1960 г., с. 149).
Равномерная нагрузка, равномерное давление 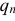 на любую кривую эквивалентна такому же давлению, действующему на хорду
на любую кривую эквивалентна такому же давлению, действующему на хорду  этой линии (рис.11.5).
этой линии (рис.11.5).
Доказывается это просто. Разложим силу 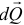 , действующую на элемент дуги длиной
, действующую на элемент дуги длиной 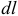 на вертикальную и горизонтальную составляющие:
на вертикальную и горизонтальную составляющие:

Тогда проекции равнодействующей 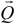 на оси:
на оси:
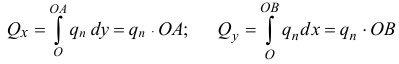
и ее величина, модуль,
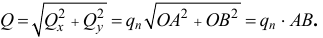
Направлена равнодействующая под углом 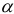 , тангенса которого
, тангенса которого
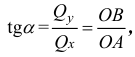
то есть перпендикулярно хорде  . Иллюстрацией к этому являются и результаты, полученные в примере в §3, гл.VI (рис.6.10).
. Иллюстрацией к этому являются и результаты, полученные в примере в §3, гл.VI (рис.6.10).
- Ну, всё, Алексей, хватит на сегодня. До сентября больше не появляйся, отдыхай.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Прямой центральный удар двух тел |
| Удар по вращающемуся телу |
| Основные определения и понятия о статике |
| Сложение системы сходящихся сил |
