Курсовая работа Д 8.0
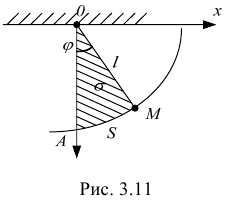
Плоский математический маятник имеет одну степень свободы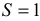 
. В качестве обобщенной координаты 
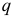можно принять: угол 
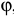, длину 
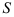дуги 
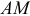, площадь 
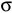сектора 
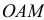(рис. 3.11).
Малые положительные приращения обобщенных координат называются обобщенными возможными перемещениями и обозначаются символами
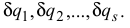
При движении системы ее обобщенные координаты будут с течением времени непрерывно изменяться и закон этого движения определится уравнениями
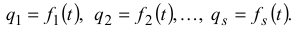
Уравнения (3.51) представляют собой кинематические уравнения движения системы в обобщенных координатах.
Производные от обобщенных координат по времени называются обобщенными скоростями системы. Их будем обозначать символами
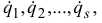
где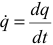 
. Размерность зависит от размерности соответствующей обобщенной координаты.
- Обобщенные силы
Рассмотрим механическую систему, состоящую из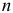 
материальных точек, движущуюся под действием сил
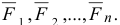
Пусть система имеет 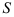степеней свободы и ее положение определяется координатами (3.50). Сообщим системе такое независимое перемещение, при котором координата 
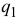получит приращение 
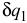, а остальные координаты не изменяются. Тогда радиус-вектор
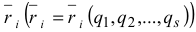
каждой точки системы получит элементарное приращение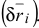 
Так как при рассматриваемом перемещении изменяется только координата 
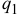(остальные сохранят постоянные значения), то 
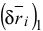вычисляется как частный дифференциал
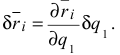
Вычислим сумму элементарных работ всех действующих сил на рассматриваемом перемещении
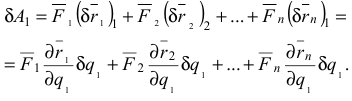
Вынесем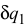 
за скобку и обозначим
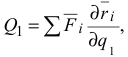
получим
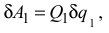
назовем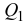 
обобщенной силой и тогда ее величина будет равна
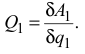
Таким образом, сообщая системе независимое возможное перемещение по каждой обобщенной координате, мы сможем определить обобщенные силы
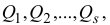
соответствующие этим обобщенным координатам.
Если системе сообщить такое возможное перемещение, при котором изменяются все обобщенные координаты, то получим
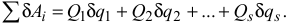
Уравнение (3.52) дает выражение полной элементарной работы всех действующих на систему сил в обобщенных координатах.
Значит, обобщенные силы — это величины, равные коэффициентам при приращениях обобщенных координат в выражении полной элементарной работы действующих на систему сил. Размерность обобщенной силы зависит от размерности обобщенной координаты и равна размерности работы, деленной на размерность соответствующей обобщенной координаты.
- Дифференциальные уравнения Лагранжа второго рода
Для вывода уравнений Лагранжа воспользуемся общим уравнением динамики (3.49)
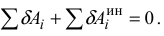
Пусть система имеет 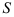степеней свободы и её положение определяется обобщёнными координатами (3.50). Тогда по формуле (3.52) имеем
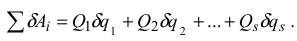
Аналогично можно получить выражение полной элементарной работы сил инерции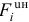 
. При этом получим
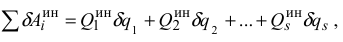
где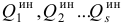 
— обобщенные силы инерции, которые равны
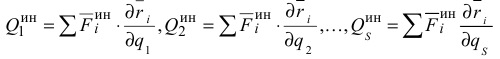
Уравнение (3.49) с учётом (3.53) и (3.54) имеет вид
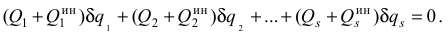
Так как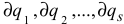 
между собой независимы, то полученное равенство может выполняться лишь при условии, когда каждый из коэффициентов при 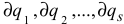в отдельности равен нулю, т. е.
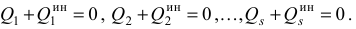
Условия (3.56) называются уравнениями Лагранжа первого рода.
Выразим все входящие в уравнения (3.56) обобщённые силы инерции через кинетическую энергию системы. Поскольку сила инерции любой из точек системы равна
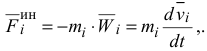
то первую формулу равенств (3.55) можно записать в виде
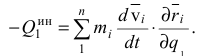
Преобразуем правую часть равенства (3.57) так, чтобы она содержала скорости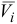 
точек системы.
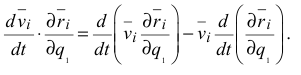
В справедливости этого результата легко убедиться, продифференцировав первое слагаемое, стоящее в правой части равенства. Дальнейшее преобразование осуществляется на основании следующих двух условий:
1) Операции полного дифференцирования по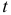 
и частного дифференцирования по 
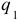переместительны, что даёт
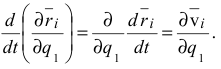
2) Частная производная от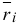 
по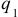 
есть предел отношения частного приращения 
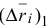к приращению 
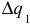, откуда получаем
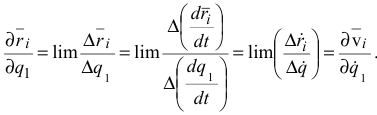
С учётом (3.58) и (3.59) равенство (3.57) представим в виде
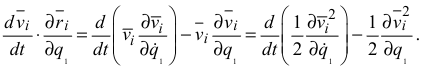
Подставим (3.59) в формулу
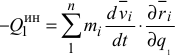
и получим
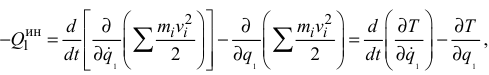
где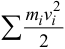 
— кинематическая энергия системы.
Аналогичные выражения получатся для всех остальных обобщённых сил инерции.
В результате равенства (3.56) примут вид
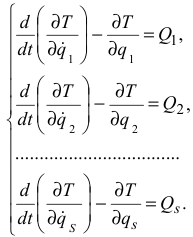
Уравнения (3.61) представляют собой дифференциальные уравнения движения механической системы в обобщённых координатах, или дифференциальные уравнения Лагранжа второго рода. Число этих уравнений равно числу степеней свободы системы.
Уравнения Лагранжа дают единый метод решения задач динамики.
