Полный дифференциал функции

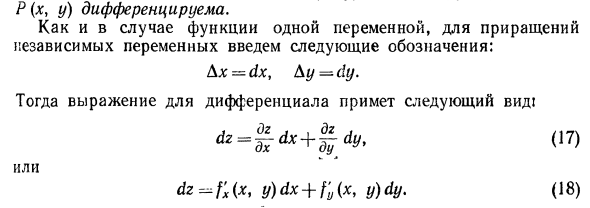
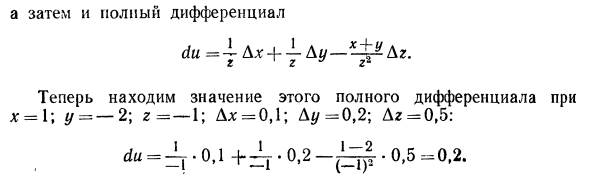
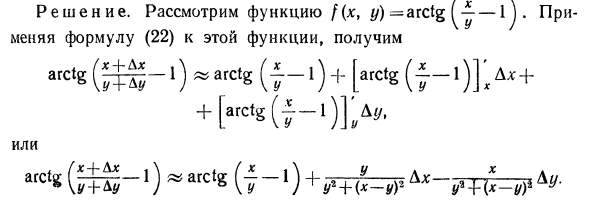
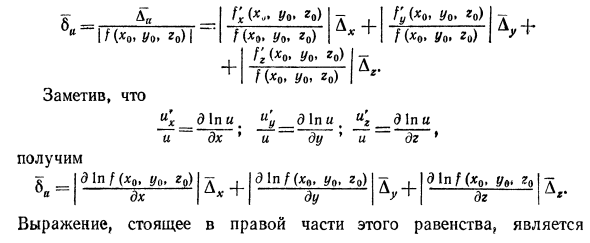
Полный дифференциал функции

• Полная разница в функции некоторых переменных. Приращение всех функций При нахождении частных производных учитывались частичные приращения функций некоторых переменных, а когда изменялся только один из аргументов, остальные оставались фиксированными (постоянными). Далее рассмотрим полное приращение, которое получает функция, когда все ее аргументы изменены.

Задайте функцию двух переменных z = * f (x> y). Функция z-f (x, y) затем получает полный инкремент Az, определяемый как: Az = f (x + Axe, y + Au) — -фикс, U). (12) Геометрически полным приращением функции Ag является график функции zf (x, y) при переходе от точки P (x \ y) к точке Px (x + Ax; y4-Ay) Равен шагу приложения (рисунок 220).

Предположим, что ее аргументы x и y получают приращения Ax и A y соответственно. Людмила Фирмаль

Пример. Если x имеет приращение Ax, а # является приращением A y, найдите полное приращение функции r-xy2. Решения. Используйте уравнение (12) для получения: И r = (x + Ax) {y + Au) 2 —xu2 = xy2 + y2 Ax + 2xuAy + 2yAxAy — \ — x (Au) 2+ + Ax (Au) r — xy2 = y2Ax + 2xuAy + 2yAxAy + x (Au) 2 + Топор (Au) \ Вы можете видеть, что общий прирост Az этой функции может быть выражен как сумма двух слагаемых. Линейен относительно приращения первого слагаемого tfAx + 2xyAy, аргументов Ax и A // и линейен относительно второго слагаемого 2yAxAy — \ — x (Au) 2 — \ — Ax (Au) r, Ax и Ay Нет Если Ax-> 0, Au- * 0, эти члены явно стремятся к нулю. Однако второе слагаемое в этом случае стремится к нулю раньше, чем первое слагаемое. Это хорошо видно из следующей таблицы. Рисунок 220

Решения. Рассмотрим функцию f (x, y) = arctg ^ -1J. • Применяя уравнение (22) к этой функции, arctg (^ -l) «arctg (f-l) + [arctg (f-l)]> + [«Dg (f-l)]>. + или arctg 1) «arctg (f -1) ^» FPF ^ Здесь x = 2 и y = 1. Тогда Ax 0.03, A * / = 0.02. так arctg 1) «arctg (y ~ 1) + i» + (Ll) » _2. Около 02 12-1- (2-1) 2 ‘ или arctan (f ^ -1) «arctan 1-y • 0,03-0,02 = i — O, 015-0,02» 0,75. Пример 2. Если центральный угол кругового сектора равен 80 °, мы хотим 15-минутное уменьшение.

• Решение задач по высшей математике

Предел функции нескольких переменных» непрерывность функции. Точки разрыва	Дифференцирование сложных и неявных функций
Частные производные	Скалярное поле

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

• На сколько я должен увеличить радиус r = 30 секунд? Решения. Область 5 кругового сектора представлена ​​следующей формулой: s i / ‘y ° ~~ 360’ Где r — радиус круга, а (p — центральный угол в градусах. Если изменение в области AS (приращение) заменяется (почти) полной разницей, По предположению, AS уменьшается до нуля, когда центральный угол уменьшается, а радиус увеличивается. Итак, мы предполагаем dS a, 0Sалд-ДГ + ^ Дф ^ О, Откуда Ds. / л G2CH> \ ‘L / -2 A 1 ^ 00) f’Af „, 360“ Af_g-Df 0S_ /лг^.улгср2ф• 57 V 360 «J g i» o » Положив / — = 30 ели, ср = 80 °; A <p = -, получить

Замечания. *, Где M — максимальное абсолютное значение частной производной второго порядка f ** (* »Y)> Gku (x>! /)> Guu (*» Y) аргументов от x до x -j- Ax и y При переходе от у к у.

Это показывает, что погрешность, полученная с помощью приближения (22), не превышает числа. d = 4 A1 (I D% | +1 d ,,!) Людмила Фирмаль

II. Покажем, как применяется производная функции нескольких переменных, чтобы найти границу между абсолютными и относительными ошибками в приближенном расчете (см. Главу 6, § 3, с.5). Пусть величина является дифференцируемой и положительной функцией трех переменных (для детерминизма) x, y и r. U = f (xt y. G). (24) Предположим, что точные значения ее аргументов x9 y, z неизвестны, но известны их приближения x09 y0, zQ9 и границы абсолютных ошибок Dd, Dy, Ar.

Как найти границу между абсолютной и относительной погрешностью функции и рассчитать по формуле (24)? Введение обозначений x — x0 = Ax9 y — y0 = Au, z — r0 = Dr, как определено границей абсолютной ошибки | Д * | <Д „| Дг / | <Ду 、 | Дг | <Дг. (25) Абсолютная ошибка функции u, очевидно, равна ее инкрементальному модулю Au = f (x0 + Ax, y0 — \ — Ay9 r0 Dr) -f (x9t y09 r0) Приблизительно равно абсолютной величине суммарной разности и: \ Au \ & \ f’x (x0, y09 z0) Ax + f’y (x0, y0, z0) Ay + f’t (x0, y09 z0) Az . В зависимости от абсолютного значения свойства I fx (* 0. Wo * o) D * + You (* o. Yo> r0) на + Tr (* „> Y» zo) ^ | <| f’x (* 0, tj0, Z0) | XX A * | + | fc (* .. Y »Zo) \ — \ by \ + \ fz (Xo, Yo> Следовательно, учитывая уравнение (25), | О Ди | <| / P * Yo> * 0) 1 + Yo * *> | A, + | / U * .. Yo> 20) \ Ar. Это Cchhh, y0> r0) \ Ax — \ (xn9 y99 z0) \ Ay + \ f’t (x0, y09 z0) | Ag (26) Вы можете выйти за пределы абсолютной ошибки. По определению относительная погрешность 6С равна:

6 .. = Я е (* о »Wo> го) я Заметили f’x (x . y o »r0) / ( o. yo, r0) /;, (* <>. Go) I -t A * + Av + fix0. y0. r0) A- + f ‘(* o> yo.go) Это f (* 0. Wo. 20) «x ^ ainu.»; = aina дх 1 и делай и ог 9 и Мы получаем A _ | dlnf (x0, y0t r0) I-e, \ d \ nf (xn, y0, r0) 0 ~ I ^ I + I- В /(x0.r0 <г Av + A- Уравнение в правой части этого равенства Граница абсолютной погрешности функции In f (x, y, z) = ■ In и. так К = А, „(27) Другими словами, границу абсолютной погрешности натурального логарифма этой функции можно рассматривать как границу относительной погрешности конкретной функции. Давайте рассмотрим пример.

Как известно из физики, период колебаний маятника T определяется уравнением T = 2n | /. Где / — укороченная длина маятника, а g — ускорение силы тяжести. Решая это уравнение для g, 8 = ^. (28) Уравнение (28) используется для расчета ускорения силы тяжести в различных точках на поверхности и измеряет укороченную длину маятника / и период T вибрации в этих точках. \ R0 = 1,4196 секунд. Предположим также, что границы абсолютной погрешности известны как D / = 0,01 и Am = 0,0001.

Необходимо рассчитать гравитационное ускорение g с помощью уравнения (28) и найти границу между абсолютной и относительной погрешностями найденного значения g. При определении ошибки следует учитывать, что в уравнении (28) необходимо получить приблизительное значение l0 числа l. Получите это число с точностью до 0,0001. То есть положить = 3.1416, Dia = 0,0001. Далее, согласно уравнениям (27) и (26), 81 = A | nv = | (1nv) i | jav | «-Aj + | (1nJ || i« Jav • A, +1 (\ ngjr | g = n, -Ar = * / = / o / = / o / = / » m = m „m-T0 m = mc 2Dl D, 2At _ 2 0,0001 0,01 2 0,0001 Lll / 1L + 3,1416 + ~ 50 «+ 1,4196 ~ U> UUU4U> Другими словами, относительная погрешность составляет 0,040%. Здесь найдите приблизительное значение g, используя уравнение (28).

4- (3,1416) а-50,00 _- (см \ — (1,4196) ^ — с того времени Af = 979,5-0,00040 * 0,4, «= 979,5 ± 0,4 В заключение рассмотрим некоторые правила приближенного расчета, вытекающие из уравнений (26) и (27). Предположим, что вы хотите получить аппроксимацию x0 и j / 0 на границе абсолютной ошибки A и Ду при измерении или расчете положительных значений x и y соответственно.

1) Когда z = x + y, AZ = AX4-Ay, дг. дециграмм Потому что 5- = 1 и m- = 1 ты делаешь Следовательно, общая граница абсолютной ошибки равна сумме границ абсолютной ошибки членов. 2) Если r = x — y, с того времени дециграмм ^ 1 = 1 д * * = 1 дг, дг д- = 1, = -1 и ты делаешь Следовательно, граница абсолютной погрешности разности равна сумме границ абсолютной погрешности, уменьшенных и вычтенных. 3) Если z = xy, то в z-In x-In- Ain r = ^ — + ^ = 6x + 6y. о Используя уравнение (27) = +

Другими словами, граница относительной погрешности произведения равна сумме границ относительной погрешности фактора. 4) Если 2 = y, вы можете получить его так же легко Другими словами, частная относительная граница ошибки равна сумме границ относительной ошибки дивиденда и делителя.

Вращение конкретной функции гг в точке P0 (1; 1) и значение ее линейной части Дх-f-2Ау и нелинейной части 2Дл «Д {/ — | — (Д //) 2 -} — 4-Дл ‘(Д ^) 2 для разных значений Да и Ду: ДхД * Д2 Линейная часть Дх + 2 Ду Нелинейная часть 2 Длг Ду + (Ду, «+ Дл (Д ^) ‘ 0,1 0,1 0,331 0,3 0,031 0,01 0,02 0,050804 0,05 0,000804 0,001 0,01 0,0211201 0,021 0,0001201 Полнофункциональный дифференциал В предыдущем абзаце приращение функции двух переменных выражается как сумма двух слагаемых, линейных и нелинейных по отношению к D * и Au, и Ax -> — 0, Au-0, нелинейная часть приращения больше Мы рассмотрели пример, который быстро стремится к нулю.

Чем линейный. Многие функции имеют сходные характеристики. Эти функции называются дифференцируемыми. Определяющая функция z = f (x, y) называется дифференцируемой в точке P (x, y), если ее полный прирост Az можно выразить в виде Az = Д-Ь-ВАВа + о) (Д:, Ау), (13) Где Ax и Au — приращения соответствующих аргументов x и y вблизи точки P. A и B — константы (то есть значения, которые не зависят от Ax и Au) ‘, co (Da; Au) бесконечно меньше точки P (расстояние между x p = V Ax2 + A y2; y ) И Pv (x + Ax \ y + Ly) (т.е. lim w (Ax * Dy) = o \ p- * oP / ‘ Таким образом, если функция z = * f (x, y) дифференцируема в конкретной точке, согласно уравнению (13), общее приращение в этой точке состоит из двух частей: •

Линейный по отношению к Dx Увеличение AAA + VAU основной части Au, а нелинейной части до (Да, Au) порядка меньше основной части приращения. Определение Основная часть приближения функции z = f (x, y), линейной по Ax и Au, называется полной производной этой функции и выражается в виде dz или df (x, y). Вот так dz = AAx- \ ~ BAy. (14) В формуле разности AAx + VAy величины A и B зависят не от Да: и Ay, а от точки P (x \ y), где эти разности учитываются. То есть A и B являются функциями x и y. Вид этих функций устанавливается следующей теоремой. Теорема * Когдафункция z = * f (x, y) отличается в точке P (x, y)

Возможно (т.е. есть производная A & x + Bhy), она имеет частную производную первого порядка в точке P (x \ y), и £ = £ = с. ты делаешь Доказательство. Согласно гипотезе теоремы, эта функция в точке P (x; y) является дифференцируемой, поэтому полное приращение Δ в этой точке определяется уравнением (13). Эта формула справедлива для достаточно малых Kx и Du. Особенно, когда ## = 0 и АхфΦ0, он остается в силе. Однако приращение функции гг является удельным приращением хх,

Формат mule (13) следующий: Axz = A Ax + co. Разделив обе части этого уравнения на Ax и передав его до предела как Dx- * 0, получим: Lim Li, н-я- Ах ах ах Указывает lim-> 0. На самом деле D * / = 0, поэтому _ Ах — ах p —YAX2 + Ay2 = | Dx |. так lim® ± iim m ^ m = ± lim- = 0 Следовательно, предельный предел существует и равен A. DDG-0 Lx lim-таким образом, частный дифференциал в точке P (x; y) -J- Ах 0 лх ах 0х Аналогичным образом можно показать, что в точке P (x; y) имеется частная производная 0 и она равна B. Замена уравнений (13) и (14) A и B частной производной ^ дает: Az ^^ от Ax-j- до Ay-fco (Ax, Ay), (15) dz- ^ Axe + ^ Ай. (16)

Вообще говоря, обратная теорема оказывается ложной. Другими словами, наличие частичной дифференциации не означает существования полной дифференциации. Однако, предполагая, что частная производная не только присутствует, но и непрерывна, функция дифференцируема. Другими словами, справедлива следующая теорема, но доказательств не приводится. Частная производная ^ теоремы функции z и 0 = f (xt y) Если оно непрерывно вблизи точки P (x, y), функция P (x, y) дифференцируемо. Как и в случае функций с одной переменной, мы вводим следующие обозначения для приращений независимых переменных: x-dxt Sy — dy. Формула дифференциации имеет следующий вид! или y) dx + f’u (x, y) dy. (18)

Все вышеперечисленное можно легко распространить на функции более двух переменных. Так, например, для дифференцируемой функции с тремя переменными u = f (x, y, z) общий прирост Di определяется как Au = Dx + * L Ay + g-Az + (o (Ax, Ay, Az) (19) Цель из lim- = 0 (p = YAX * + Aug + Ai5), p-o P l Его полная производная + (20, Пример 1. Найти полную производную функции z — xy1 в любой точке. Решения. Общая производная dz = ^ dx + ^ dtj существует Тема частичного дифференцирования непрерывности ^ и

Найти g £ y = (xy% = 2xu. Вы можете видеть, что найденные частные производные являются непрерывными функциями по всей плоскости Ox //. Таким образом, производная этой функции существует везде, dz ~ y2dx + 2hu dy. Пример 2. Нахождение значения полной производной функции И х-1; у-2; r = -1; Dx = 0,1; D * / ^ 0,2; Dg = 0,5. Решение: найти частные производные g g dg V g g * ‘

И полный дифференциал du = -j Axe + y Ay— ^ Dg. Здесь, если x = 1, найдите значение этой общей разницы. y = -2; r = -1; Ax = 0,1; Au = 0,2; Dg = 0,5: du =. О, один 0,2 • 0,5 = 0,2. Применение полной дифференциации для приближенных расчетов I. Полная дифференциация нескольких переменных функций Может использоваться для приблизительных расчетов.

Давай дадим Дифференцируемая функция z = f (x, y). Его полный шаг представлен выражением A * = f * (, Y) и x + Gu (x. Y) и Y + Du). Где co (Ax, Au) есть p = | / A (Dx) d + (D //): Стремиться к нулю быстрее, чем. Поэтому слагаемые small p, т.е. small | Dx | и | Af / |, co (yes, Au), можно игнорировать. »£ (. Y) Ax + Gu (x, y) Au, (21) Это означает, что приращения функций могут быть почти полностью заменены их полными различиями. Так как r = f (x, y) Dt = f (x + DA, y -} — Ay) -f (x, y). Подстановка этого уравнения для Az в уравнение (21) дает: f (x + Ax, y + Ay) -f (Xt y) </; (x, y) Ax + f’y (x, y) Au, Откуда f (x + Ax, y + Ay) // (a , y) /; (x, y) Ax + f’y (x, y) Au. (22) В уравнении (22) значением функции и ее частной производной являются точки P (a; y). Аналогичные уравнения могут быть выведены для функций n переменных с η> 2. Например, если η = 3: Cx + Ax, y + Au, z + Az) & f (x, y, z) + f’x (x, yt z) Ax + f’y (x, y, z) Ay + + /; (, Y, z) Az. (23) Пример 1. Примерный расчет с использованием полного дифференциального arctg (j — ^ — 1).