Оглавление:







Полуэмпирические методы решения задач о свободной турбулентности
Полуэмпирические методы решения задач о свободной турбулентности. Понятие свободной турбулентности обычно контрастирует с понятием париетальной турбулентности. Наиболее характерными примерами свободной турбулентности являются турбулентность в струе (в движущейся неподвижной жидкости) или следы движущегося тела. В разделе 18.2 уже отмечалось, что при достаточном удалении от стенки, вне логарифмического слоя трубы и пограничного слоя пластины, течение характеризуется также свободной турбулентностью, параметры которой практически не зависят от расстояния до твердой границы. В данном разделе рассматриваются возможности, предлагаемые уравнением Рейнольдса, их полуэмпирические методы решения простейших задач свободной турбулентности и основные методы их решения problems.
Полуэмпирический метод замыкания уравнения Рейнольдса эффективен только при решении задачи о распределении средней продольной скорости в двух областях. Людмила Фирмаль
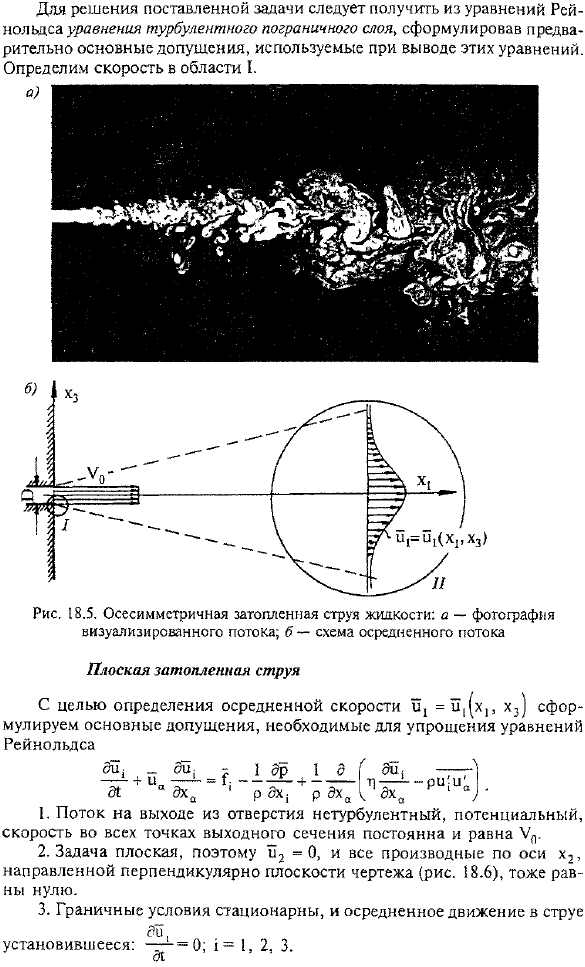
- As упомянутое выше, нас в первую очередь интересует распределение средней скорости. Отметим, что в случае свободной турбулентности молекулярная вязкость при расчете поля средних скоростей пренебрежимо мала и рассматривается только так называемый молярный транспортный процесс, обусловленный случайным движением турбулентности основного объема жидкости. В качестве примера рассмотрим вытекание жидкости с постоянным потоком из круглого отверстия в полупространство, занимаемое той же жидкостью в состоянии покоя (рис.18.5). Область / находится близко к краю отверстия. Здесь течение в этой области можно считать плоской потоковой турбулентной струей, игнорирующей кривизну круглого отверстия.
Область/ / расположена на значительном расстоянии от отверстия, когда влияние некоторых особенностей начальных условий (например, распределение скорости на выходе из отверстия) незначительно. Поток здесь описывается как осесимметричный погруженный поток, находящийся далеко от отверстия. Неравномерное течение каждой из этих областей является границей layer. In область I, этот слой отделяет невозмущенный равномерный поток от пространства, занятого отверстием и неподвижным liquid. In область II, все стороны пограничного слоя окружены неподвижной жидкостью. Плоский поток потока Чтобы определить среднюю скорость ω1= [[(x1, x3), сформулируйте основные допущения, необходимые для упрощения уравнения Рейнольдса 1.Поток на выходе из скважины является нетурбулентным, потенциальным, а скорость во всех точках выходного сечения постоянна, равна UL. 2.
- Так как задача плоская, и вдоль оси Х2 все производные, направленные перпендикулярно плоскости чертежа (рис.18.6), также будут равны нулю. 3.Граничные условия являются стационарными и означают движение внутри струи Да. Это было установлено. 4.Исключите из рассмотрения внешние объемные силы. 5.Do не вводите молекулярную вязкость в расчет. Потому что、 Свободная турбулентность 6.Рассмотрим постоянное давление для всей площади. p = saps следующие 3 предположения характерны для теории границ: В этом слое обычно принято, что все свойства турбулентного потока быстро изменяются во всем потоке, медленно изменяясь вдоль потока. В предположении 3 уравнений Рейнольдса (17.19) и несжимаемых уравнений (17.18) получаем 2 уравнения. Система (18.62)является уравнением турбулентного пограничного слоя.
Очевидно, что скорость в любой точке рассматриваемой области зависит от физических характеристик жидкости(т. е. ее плотности и вязкости) и величины скорости V0, поэтому можно рассчитать x〜x (игнорируя вязкость при свободном турбулентном течении) (p> V0, x, x3). Размерный анализ、 Используйте размерный анализ для определения зависимости между турбулентным касательным напряжением ri [U3 = p31 и функцией G. P3 на каждом поперечном сечении пограничного слоя! Постоянно, то есть p3! он не зависит от Х3.Тогда естественно рассмотреть Из анализа измерений это выглядит следующим образом Где c-универсальная постоянная. (18.63) если вы замените (18.66) на (18.62)、 Формула (18.67) делится на 2 Формулы.
Очевидно, что решение уравнения является линейной функцией, но функция потока, удовлетворяющая начальным и предельным условиям, принимает вид. Людмила Фирмаль
- Эта функция показывает распределение скорости вне пограничного слоя (рис. 18.6). Решая уравнение (18.69), вы должны быть в состоянии найти распределение скорости в пограничном слое и, следовательно, контур этого boundary. It необходимо сформулировать условие на этих границах и, согласно (18.64), быть прямой линией (плоскостью X [0×3).Рассмотрим уравнение верхней границы x3 = E, A-X], а нижней границы x3 = * x|;.%Значение, а затем Определить из решения уравнения (18.69). на границе пограничного слоя функция u =их ^ (X3) и ее производная должны быть непрерывными. Непрерывность функции от I! Должен Но от непрерывности его производных. Кроме того, в соответствии с предельными условиями, такими как x3-> oo, вам нужно поместить=то на верхнюю границу непрерывности функции.
Смотрите также:
Примеры решения задач по гидравлике
Возможно эти страницы вам будут полезны:
