Оглавление:







Полуэмпирические выражения для напряжений Рейнольдса
- Учитывая определенный тип турбулентности импульса τ, мы можем использовать уравнение (5.13) для нахождения профиля скорости P. Различные авторы предложили некоторые полуэмпирические представления этого потока(см. ниже). Эти выражения могут ссылаться на первоисточник. Кустистость вихревой вязкости [5]. Уже в прошлом веке по аналогии с законом вязкости Ньютона было решено описать выражение течения в следующем виде: (5.14) q (P обычно называют «коэффициентом турбулентной вязкости» или «вихревой вязкостью», как правило, это значение практически зависит от пространственных координат.
Путь смешения Прандтля [6]. Прандтль предположил, что частицы турбулентной среды совершают случайное движение, подобно молекуле газа, с постоянным тепловым движением (конечно, эта аналогия очень далека).Основываясь на этой гипотезе, он вывел формулу, описывающую передачу импульса. 1(1 ух(ух 1 & 1 БУ (5.15)} Здесь величина, называемая смешанным путем r, грубо говоря, играет ту же роль, что и средний свободный путь молекулы в кинетической теории Гаэ. Путь перемешивания примерно такой же, как и «вихревая вязкость», но определяется координатами. Прантл проанализировал характеристики турбулентности вблизи твердой стенки и предположил, что величина I линейно зависит от расстояния y от стенки.
Рекомендуется, чтобы значения физических параметров определились по температуре, подсчитанной по формуле (8-16). Людмила Фирмаль
То есть, я записал это количество выражений в виде/ = xxu. It следует отметить, что аналогичная связь с формулой (5.15) также выводится из теории переноса вихревого напряжения Тейлора[7]. Гипотеза подобия кармана[8, 9].Исходя из соображений размерности, Калман вывел следующее уравнение для напряжения Рейнольдса: Я (Ю/Ю) 9 (Да/ f) 9 (5.16 )) Здесь x2-универсальная константа, равная 0,36-0,40 на основе различных авторских экспериментов (граница интервала определяется по экспериментальным данным о профиле скорости круглой трубы).
Эмпирическая формула десслера для течения теменной части [9].Формулы Прандтля и кармана неприменимы в турбулентных областях в непосредственной близости от твердых стенок. Это связано с тем, что эффект молекулярной вязкости играет определенную роль в его близости. Для этой области дислер предложил эмпирическую формулу * ух = -ПН2 ^ ху(1-ехр (- nxu / г)} Ага. 1-летний (5.17)) Где n-эмпирическая constant. By измерив распределение скорости потока в трубе, Дайель Эр обнаружил, что n равно 0,124. В следующем примере показано, как использовать эмпирическую зависимость напряжения Рейнольдса для получения информации о свойствах турбулентности.
Заметим, что многие авторы игнорируют и упрощают эффект кривизны при применении указанного соотношения к криволинейной системе. Если это упрощение невозможно, то соответствующее выражение должно быть записано в криволинейных координатах. В связи с вышеизложенным, величина m (×Тензор form. It полезно представлять, например, для гипотезы подобия кармана тензорное представление потока является Общее соотношение, полученное этим исследователем, выглядит следующим образом: (5.18) Где D (/=[dU1 / dx1])+(du ^ dx ^ Y / y =(di ^ dx ^ by u>(задается компонент Ротора поля средней скорости, т. е. u> = [V e] количество (D; D) и (d; d) — скалярное произведение соответствующего тензора.
В плоском параллельном потоке со сдвигом уравнение (5.18) совпадает с уравнением (5.16).Для осесимметричного течения в трубе с полем скоростей, определенным в соотношениях r2 = p2 ® и= pr = 0, Формула(5.18)принимает вид: (5.19)) Для тангенциального течения между двумя вращающимися цилиндрами, если компоненты поля скоростей удовлетворяют соотношениям ® и\ = \ = 09, то из уравнения (5.18) мы видим следующее: Последняя формула точно соответствует соотношению, полученному Кальманом[10]. Пример 5-1. Выведение логарифмической формулы профиля скорости трупа (вдали от стены).
Это усредненное по времени распределение скорости турбулентности в длинной трубе с использованием гипотезы Прандтля о смешивающем пути. Радиус и длина трубы будут равны I и L. (5.20 утра)) Решение. 8 — — — в r укажите расстояние от стенки трубы, предположим I = uc8.Тогда, согласно соотношению (5.15), проекция вектора импульсного потока на ось x 。( _ * )•, (5.21> Явную форму уравнения движения можно получить из общего уравнения(5.13).Если несжимаемая жидкость течет с профилем скорости p3 = p, то (r>уравнение движения описывается следующим образом: РО-Пи-1 а Где хп = х% Это уравнение легко интегрируется.
Используя условную границу xy = 0 с r = 0, можно увидеть следующее: Т» = (По〜ПБ) л 2б г (5.23) Черный?3 он показывает напряжение сдвига стенки трубы( $-0). в основной области турбулентного ядра, или изменения координат, вклад молекулярных компонентов потока пренебрежимо мал по сравнению с вкладом турбулентной составляющей m. другими словами, в указанных областях перенос импульса осуществляется в основном турбулентными вихрями. Поэтому, если вы хотите учесть турбулентное ядро, подставьте значение[опорная формула-(5.21)]. в результате.
- Прандтль ввел математическое упрощение выражения (5.24) (физически невозможное вообще) и установил правую часть выражения равной m0. Это упрощение делает его еще более простым для вычисления и может быть легко проверено путем точного интегрирования этого уравнения, что приводит к очень малым ошибкам в конечном счете result. So, можно ли проще описать уравнение движения, ограничив его приведенным выше приближением? После удаления простого кинетического уравнения det 110 _ ±1 ед » & 3 X1 8 (5.25 )) Что касается смысла, то здесь, очевидно, есть только знак плюс.
Входящий Если ХРл представляет количество у, = / т0 / р в единицах скорости、 Интегрируйте GL y V (e » 2o) и в пределах предела от внешней границы интегрируйте буфер 5 51 до любого значения a, затем、 (5.26) Или безразмерной величины р + «р ^ / р, и S * =» п ^ п / ц: Т + » П ’ = ^ 1П (’7г) (5.27} Основываясь на анализе экспериментальных данных по распределению, Дайслер быстро установил, что наиболее вероятное число констант x в трупе равно 0,36.Мы пришли к выводу, что наиболее удобно использовать значение −26 в качестве внешней границы буферного слоя boundary= 12.85).Присвоение указанного значения выражению (5.27) даст отношение K’.
В качестве определяющей скорости берут среднюю скорость движения среды в самом узком сечении между трубами. Людмила Фирмаль
Ряд исследований показал, что логарифмическое распределение (5.28) достаточно хорошо объясняет профиль скорости турбулентного числа Рейнольдса Ke> 20 000(за исключением узкой области непосредственно у стенки трубы, конечно). Пример 5-2.Распределение скорости движущегося потока по трубе(вблизи стенки).Использовать эмпирическую формулу dieseler для расчета профиля скорости ламинарного подслоя и буферной области. Solution. In область течения, непосредственно примыкающая к стенке трубы, является суммой ламинарного течения, определяемого законом Ньютона вязкости, и турбулентности, описываемой предположениями, сделанными эмпирической формулой дайслара.
Если вы добавите эти потоки, вы увидите следующее: МН = — п — ^ — пн ^ р (р-р) {1-ехр [- н ^(р-р) м)(5.29) Подставьте формулу (5.23) в Формулу (5.29) и замените разность 1 — __(s / N) на 1 (последняя операция на участке у стены вполне оправдана, так как она находится в R). в результате вы получите: М0 = п + ПН ^(1-ехр(-n2p> / г)) (5.30) Интегрируем последнее уравнение в диапазоне любого значения от s = 0 до C.
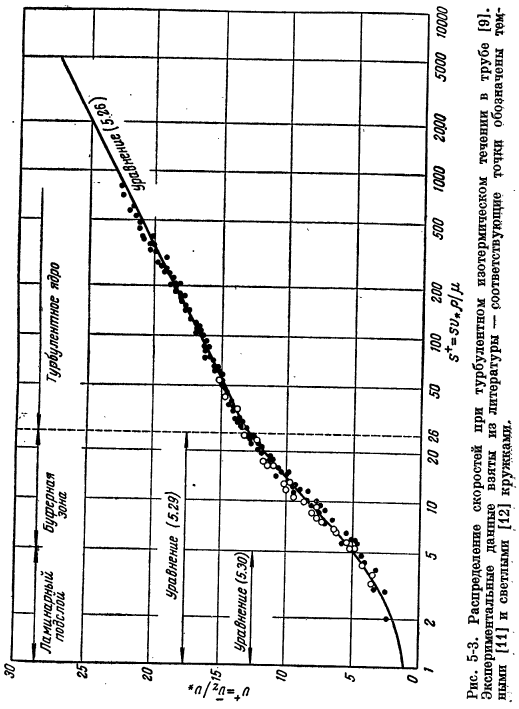
Безразмерная переменная, Интеграл результата имеет вид: −5. Унция * (1-exp (- n2y +» *)} (0 дюймов * 26) (5,31 дюйма)) Согласно имеющимся данным, эмпирический параметр n, содержащийся в этом Интеграле длинной гладкой трубы, равен 0,124.Интеграл (5.31) может быть вычислен методом последовательного приближения. Результаты расчета показаны на рисунке 5 с диаграммой зависимости V +от Альфа+. 5-3. При малых значениях 5* Интеграл (5.31) может быть вычислен аналитически. п + = б +(0 ^ б + ^ 5) (5.32) Аналогичные результаты получены путем интегрирования уравнений, представляющих законы вязкости Ньютона по толщине ламинарного подслоя.
Экспериментальные данные по распределению скоростей движения трупа при He> 20000 хорошо согласуются с расчетной кривой, приведенной на рисунке. 5-3.Читатель найдет в литературе[13]критический обзор экспериментальных исследований по определению профилей скоростей в трубах. Шероховатость стенки трубы может существенно повлиять на распределение скорости. Эффект шероховатости подробно изучался во многих теоретических и экспериментальных исследованиях.
Обширная информация по этому вопросу содержится в монографиях, приведенных выше[1].Это в дополнение к анализу потока в трубе — сяцилиндры вращения вращения и фиксированные = — ППС обсуждение упомянутых вопросов выходит за рамки настоящего » примера 5-3.Соотношение молекул и турбулентности ИЗЗ ° ° гт2!!! ^Отношениеотношение-это отношение = = 0,5 суток к турбулентности воды ^ / / при. Простите? В Радиус трубы H = 7,62 см; напряжение сдвига стенки 19 ′ 6D ^ X din? см-а; плотность Р = 1 г-см −3; Кинематическая вязкость V-0,01 см * с. Решение.
Вихревая вязкость определяется соотношением — _and ^ — и») — ^ =(P + M (0) 4 ^ m » — и Из уравнения(5.33) можно найти отношение n (P / P, выраженное в безразмерных переменных p +и$+, введенных выше. П «> 1 т». 1 ТР (1-* / I) _4_1цуд-4(5.34) Т = Уя Ли * ’ «=0.5 I, переменная » +принимает значение «’ .P_py ^ О / Р _lyak / х 2р Используйте соотношение (5.28) для вычисления производной^ / Ж * * для$ * = 485:(5.36) (5.33) (5.35 утра)) 0.36-485 Если вы подставите это значение в выражение (5.34), вы найдете следующее выражение: и =° ’362 ^-1 ^ 86 Первый Хноткохс ^^ еразыгрывается в турбулентном транспорте.
Смотрите также:
