Оглавление:
Пусть на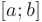 
задана непрерывная функция 
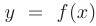. Разобьем отрезок 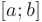точками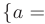 
на 
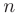элементарных отрезков 
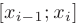. Тогда, обозначив длину элементарных отрезков как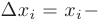 
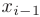и выбрав на этих отрезках произвольные точки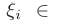 
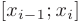можно составить для функции 
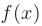так называемую интегральную сумму:
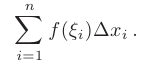
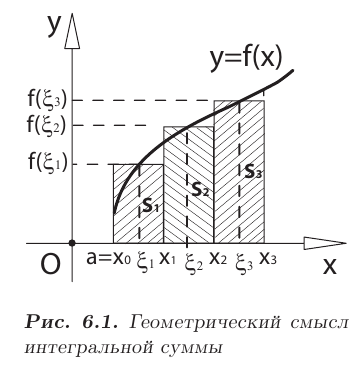
Геометрический смысл интегральной суммы. Пусть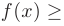 
0 на 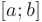. Каждое слагаемое 
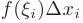интегральной суммы равно площади 
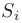прямоугольника со сторонам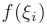и 
и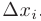 
. Поэтому интегральная сумма равна сумме площадей всех прямоугольников 
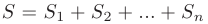(рис. 6.1).
Определенным интегралом от функции 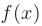на отрезке 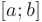называется предел ее интегральной суммы при длине наибольшего из отрезков стремящейся к нулю 
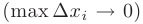, если этот предел существует, конечен и не зависит от способа разбиения отрезка 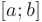на элементарные отрезки и выбора точек 
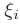. Формально этот факт обозначается следующим образом:
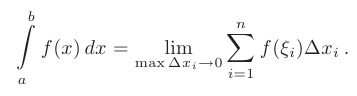
Числа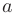 
и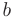 
называют нижним и верхним пределами интегрирования. Из приведенного определения следует, что определенный интеграл зависит от вида подынтегральной функции 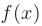и значений пределов интегрирования 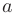и 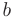, но не зависит от выбора переменной интегрирования:
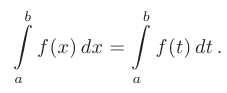
Геометрический смысл определенного интеграла
Если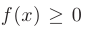 
на 
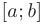, то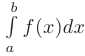 
численно равен площади под кривой 
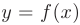на 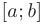(см. рис. 6.1). Действительно, при 
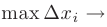0 ломаная, образованная на каждом из отрезков 
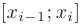прямой 
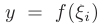параллельной оси 
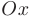, неограниченно приближается к кривой 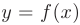. Площадь под ломаной переходит в площадь под кривой.
Свойства определенного интеграла
- Постоянный множитель
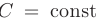можно выносить за знак определенного интеграла:
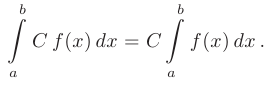
- Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме определенных интегралов от каждого из слагаемых:
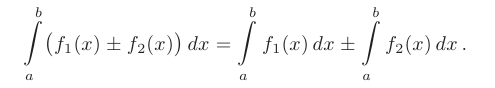
- При перемене мест верхнего и нижнего пределов знак определенного интеграла меняется на противоположный:
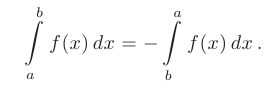
- При совпадении верхнего и нижнего пределов значение определенного интеграла равно нулю:
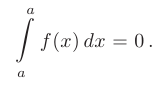
- Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых
:
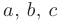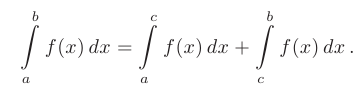
- Если для двух функций на отрезке 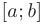верно неравенство
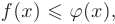, то такое же неравенство будет верно и для определенных интегралов от этих функций:
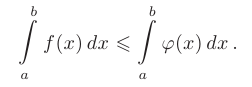
- Если функция 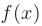непрерывна на отрезке 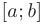, то на этом отрезке найдется хотя бы одна точка
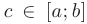. для которой будет справедливо равенство:
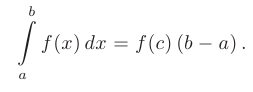
Вычисление определенного интеграла
Вычисление определенных интегралов как предела интегральной суммы часто затруднительно и значительно упрощается, если использовать формулу Ньютона-Лейбница. Если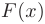 
— первообразная для непрерывной на 
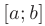функции 
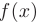, то определенный интеграл от этой функции 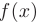равен приращению любой ее первообразной 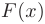на этом отрезке, т.е.:
Как и в случае неопределенного интеграла использование замены переменной позволяет упростить интеграл, приблизив его к табличному. При этом нет необходимости возвращаться к исходной переменной интегрирования, а следует найти пределы интегрирования для новой переменной.
Если функция 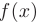непрерывна на отрезке 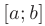, а функция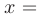 
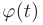непрерывно дифференцируема на отрезке 
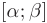, причем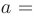 
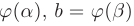. Тогда справедлива формула замены переменной в определенном интеграле:
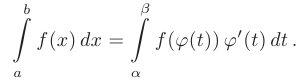
Если функци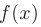и 
и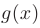 
имеют непрерывные производные на отрезке 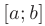, то справедлива формула интегрирования по частям в определенном интеграле:
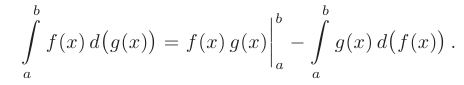
Пример:
Вычислить определенный интеграл с помощью формулы Ньютона-Лейбница
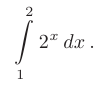
► Произвольная первообразная для функции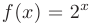 
имеет вид:
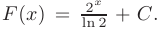
При вычислении по формуле Ньютона-Лейбница возьмем такую первообразную, у которой константа интегрирования равна нулю: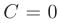 
. В результате получим:
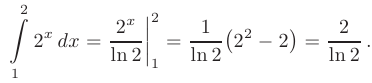
Пример:
Вычислить определенный интеграл методом замены переменной
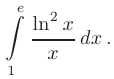
► Заметим, что множитель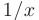 
представляет собой производную функции натурального логарифма. Поэтом}’ используя замену переменной вида 
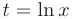, вычислим ее дифференциал
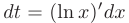
и выполним их подстановку в подынтегральное выражение:
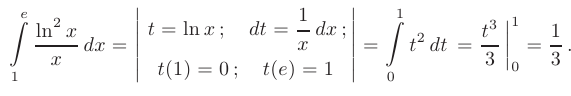
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Интегрирование рациональных дробей в математике |
| Интегрирование иррациональных функций в математике |
| Понятие о несобственных интегралах в математике |
| Вычисление площади плоской фигуры в математике |
