Оглавление:
Задача 2.90.
Построить главную задачу для задачи, состоящей в определении максимального значения функции
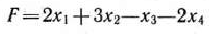
при условиях
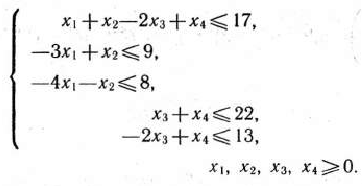
Система ограничений сформулированной задачи имеет блок-связку, определяемую первым неравенством, и два блока, первый из которых определяется вторым и третьим неравенствами системы (127), а второй — четвертым и пятым неравенствами. Следовательно,
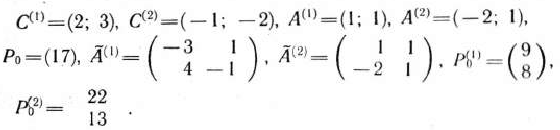
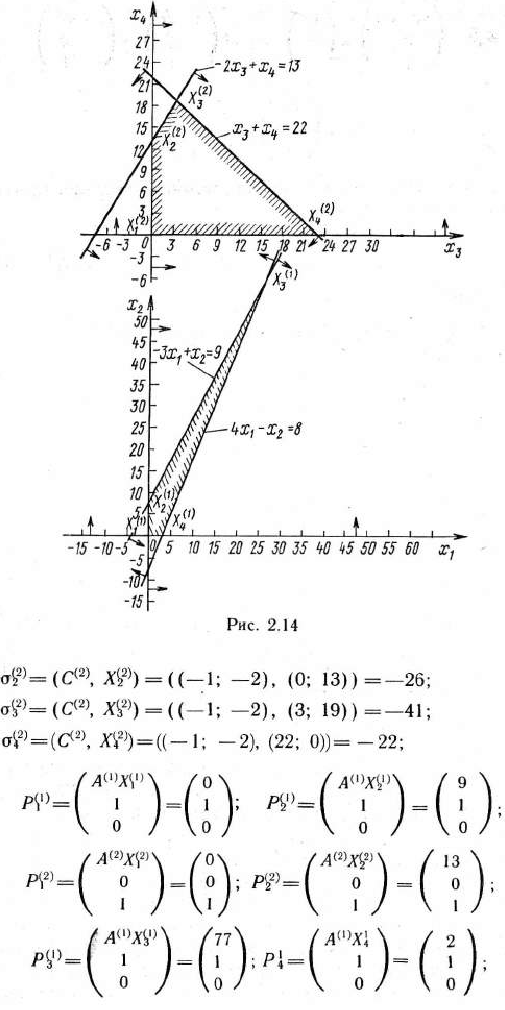
Найдем вершины многоугольников решений 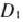 и
и 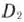 , определяемых системами неравенств:
, определяемых системами неравенств:
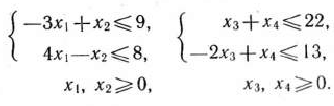
В данном случае это легко сделать геометрически. Из рис. 2.14 следует, что
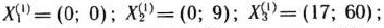
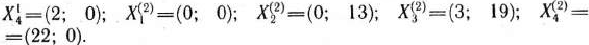
По формулам (119) к (120) получаем:
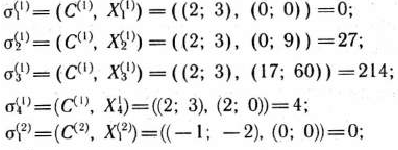
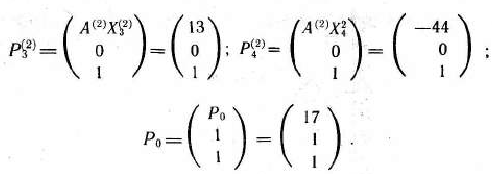
Таким образом, главная задача состоит в определении максимального значения функции
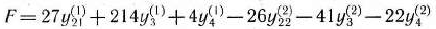
при условиях
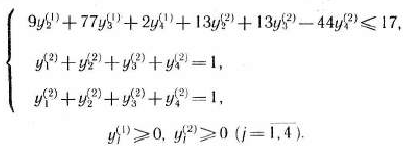
Запишем главную задачу (129) — (131) в форме основной задачи линейного программирования: найти максимальное значение функции
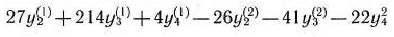
при условиях
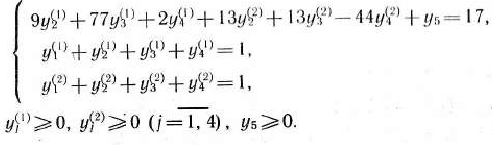
Если теперь сопоставить между собой задачи (126) — (128) и (129) — (131), то видим, что число ограничений-неравенств в первой задаче равно 5 и число переменных равно 4, а во второй эти числа соответственно равны 3 и 8. Таким образом, при переходе от задачи (126) —(128) к задаче (129) —(131) уменьшилось число ограничений, однако возросло число переменных. К тому женам понадобилось определить все вершины многогранников решений 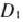 и
и 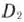 что не всегда возможно сделать так просто. Поэтому естественно возникает вопрос: стоит ли при нахождении решения задачи (126)—(128) переходить к определению оптимального плана задачи (129) — (131)? Положительный ответ на этот вопрос дает метод Данцига—Вулфа, позволяющий находить решение главной задачи (129) — (131), не зная при этом ни всех вершин многоугольников решений
что не всегда возможно сделать так просто. Поэтому естественно возникает вопрос: стоит ли при нахождении решения задачи (126)—(128) переходить к определению оптимального плана задачи (129) — (131)? Положительный ответ на этот вопрос дает метод Данцига—Вулфа, позволяющий находить решение главной задачи (129) — (131), не зная при этом ни всех вершин многоугольников решений 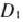 и ни их числа, а зная лишь какой-нибудь базис, определяющий план задачи (129) — (131). На этом методе и остановимся более подробно. А именно: используя его, рассмотрим нахождение решения главной задачи (121) — (123), построенной для задачи (115) — (117). В связи с этим отметим, что для начала итерационного процесса решения задачи (121) —(123) достаточно знать какой-нибудь базис, определяющий опорный план данной задачи. Этот базис можно либо непосредственно записать, либо определить его, например, используя метод искусственного базиса.
и ни их числа, а зная лишь какой-нибудь базис, определяющий план задачи (129) — (131). На этом методе и остановимся более подробно. А именно: используя его, рассмотрим нахождение решения главной задачи (121) — (123), построенной для задачи (115) — (117). В связи с этим отметим, что для начала итерационного процесса решения задачи (121) —(123) достаточно знать какой-нибудь базис, определяющий опорный план данной задачи. Этот базис можно либо непосредственно записать, либо определить его, например, используя метод искусственного базиса.
Итак, пусть известны базис, определяющий один из опорных планов главной задачи, и 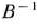 — матрица, обратная матрице, составленной из компонент базисных векторов. Для проверки данного опорного плана на оптимальность найдем вектор
— матрица, обратная матрице, составленной из компонент базисных векторов. Для проверки данного опорного плана на оптимальность найдем вектор
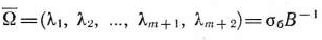
и обозначим через 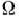 вектор, составленный из первых
вектор, составленный из первых 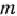 компонент вектора
компонент вектора 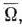 т. е.
т. е. 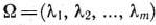 После этого найдем решение задачи, состоящей в определении максимального значения функции
После этого найдем решение задачи, состоящей в определении максимального значения функции
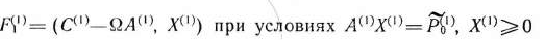
и определяемой первым блоком исходной задачи (115)—(117) (подзадача 1). Если она имеет оптимальный план 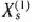 и
и 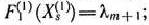 то находим решение подзадачи 2:
то находим решение подзадачи 2:
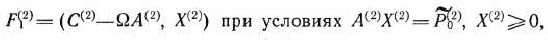
определяемой вторым блоком задачи (115) —(117). В том случае, если и эта задача имеет оптимальный план 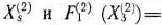
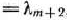 то исходный базис определяет оптимальный план главной задачи (121) —(123) и, таким образом, найдено ее решение, а следовательно, по формулам (125) и(126) можно определить оптимальный план исходной задачи (115)—(117).
то исходный базис определяет оптимальный план главной задачи (121) —(123) и, таким образом, найдено ее решение, а следовательно, по формулам (125) и(126) можно определить оптимальный план исходной задачи (115)—(117).
В тех случаях, когда
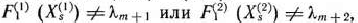
исходный опорный план не является оптимальным и необходимо перейти к новому базису, определяющему некоторый следующий опорный план главной задачи. Если при этом оказывается, что
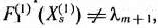
то находить решение второй подзадачи не имеет смысла.
Итак, пусть, например,
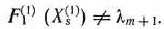
Тогда следует перейти к новому базису, определяющему некоторый последующий опорный план главной задачи. Для этого нужно какой-нибудь вектор исключить из базиса и ввести вместо него новый вектор. Вектор, вводимый в базис, определяется наименьшим отрицательным числом из чисел
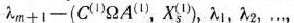
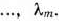
Если таким числом является  то в базис вводим вектор
то в базис вводим вектор 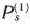 . Если же это есть некоторое число
. Если же это есть некоторое число 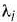 то в базис вводим вектор
то в базис вводим вектор 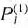 . определяемый данным числом.
. определяемый данным числом.
После нахождения вектора, вводимого в базис, определяем вектор, исключаемый из него. Для этого находим разложения векторов 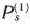 (или
(или 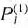 ) и
) и 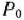 (вектор, определяющий опорный план главной задачи) по векторам данного базиса и определяем минимум отношения компонент вектора
(вектор, определяющий опорный план главной задачи) по векторам данного базиса и определяем минимум отношения компонент вектора 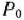 к соответствующим положительным компонентам вектора
к соответствующим положительным компонентам вектора 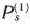 в данном базисе. Наименьшее из этих отношений и определяет вектор, исключаемый из базиса. В результате получается новый базис, определяющий последующий опорный план главной задачи. Этот план проверяем на оптимальность, для чего строим соответствующую подзадачу (подзадачи) и находим решение. Данное решение позволяет сделать вывод, является ли соответствующий опорный план оптимальным или нет. Если он не оптимален, то по описанным выше правилам переходим к новому базису, определяющему некоторый последующий опорный план. При этом заметим, что в ходе итерационного процесса возможен случай, когда среди компонент разложения вектора
в данном базисе. Наименьшее из этих отношений и определяет вектор, исключаемый из базиса. В результате получается новый базис, определяющий последующий опорный план главной задачи. Этот план проверяем на оптимальность, для чего строим соответствующую подзадачу (подзадачи) и находим решение. Данное решение позволяет сделать вывод, является ли соответствующий опорный план оптимальным или нет. Если он не оптимален, то по описанным выше правилам переходим к новому базису, определяющему некоторый последующий опорный план. При этом заметим, что в ходе итерационного процесса возможен случай, когда среди компонент разложения вектора 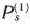 по векторам данного базиса не имеется положительных. Это означает, что целевая функция главной задачи на множестве ее допустимых решений не ограничена, а следовательно, не ограничена и целевая функция исходной задачи.
по векторам данного базиса не имеется положительных. Это означает, что целевая функция главной задачи на множестве ее допустимых решений не ограничена, а следовательно, не ограничена и целевая функция исходной задачи.
В результате после конечного числа шагов либо устанавливаем неразрешимость, либо находим оптимальный план главной задачи, а следовательно, и решение исходной задачи.
Выше рассмотрено нахождение решения задачи линейного программирования с блочной структурой для случая двух блоков. Если число блоков больше двух и равно, например, к, то алгоритм решения такой задачи, по существу, отличается лишь тем, что теперь в общем случае на каждой итерации приходится решать не две подзадачи, а к подзадач. Однако если решение одной из подзадач показало, что данный базис не определяет оптимальный план главной задачи, то находить решение других подзадач не имеет смысла.
Задача 2.91.
Найти решение задачи 2.90, состоящей в определении максимального значения функции
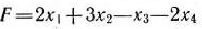
при условиях
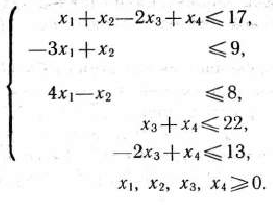
Решение:
Запишем исходные данные в матричном и векторном виде:
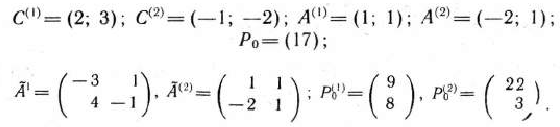
Определим теперь базис главной задачи (эта задача была записана выше).
Так как блок-связка в системе ограничений (136) задачи (135) —(137) представляет собой неравенство вида 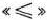 , то такой же вид примет и первое ограничение в главной задаче. Следовательно, приводя главную задачу к задаче, записанной в форме основной задачи линейного программирования, добавляем к правой части первого ограничения дополнительную переменную, которую обозначим через Этой переменной соответствует единичный вектор
, то такой же вид примет и первое ограничение в главной задаче. Следовательно, приводя главную задачу к задаче, записанной в форме основной задачи линейного программирования, добавляем к правой части первого ограничения дополнительную переменную, которую обозначим через Этой переменной соответствует единичный вектор
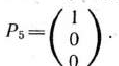
Далее, из системы неравенств
Поскольку вектор свободных членов главной задачи (136) задачи (135) —(137) видно, что многоугольники решений, определяемые соответственно первым и вторым блоками, имеют вершины
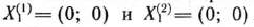
Этим вершинам соответствуют векторы
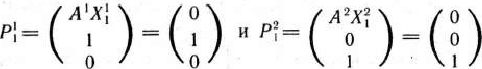
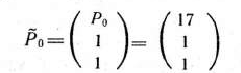
не имеет отрицательных компомент, векторы
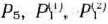
образуют базис, определяющий опорный план главной задачи, в котором отличные от нуля компоненты таковы:
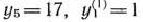
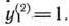
Чтобы проверить, определяет ли найденный базис оптимальный план главной задачи, найдем максимальное значение функции
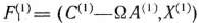
при условиях
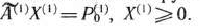
В данном случае 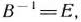 , поскольку матрица
, поскольку матрица 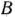 состоит из компонент единичных векторов
состоит из компонент единичных векторов
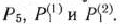
Далее,
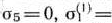
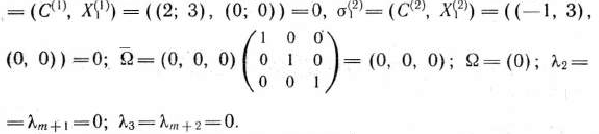
Составляем и решаем подзадачу 1:
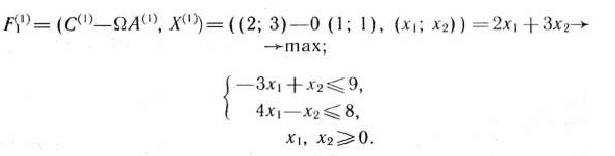
Оптимальным планом последней задачи является 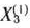 =(17; 60). При этом
=(17; 60). При этом
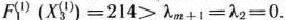
Значит, исходный базис, образованный векторами
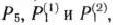
определяет опорный план главной задачи, который не является оптимальным.
Первая большая итерация, Из чисел
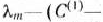
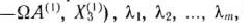
т, е. в данном случае из чисел —214 и 0, наименьшим отрицательным является —214. Следовательно, в базис вводим вектор
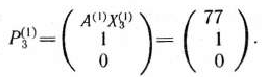
Для него
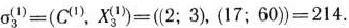
Разложение вектора 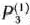 как и вектора
как и вектора
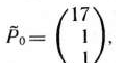
по векторам исходного базиса совпадает с этими векторами. Поэтому для определения вектора, исключаемого из фазиса, находим наименьшее из отношений компонент вектора 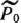 к положительным компонентам вектора
к положительным компонентам вектора 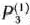 т. е. min (17/77; 1/1) =17/77. Таким образом, из базиса исключаем первый вектор, т. е. вектор
т. е. min (17/77; 1/1) =17/77. Таким образом, из базиса исключаем первый вектор, т. е. вектор 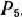 , и, следовательно, новый базис образуют векторы
, и, следовательно, новый базис образуют векторы 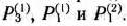 Матрица, составленная из компонент этих векторов, такова:
Матрица, составленная из компонент этих векторов, такова:
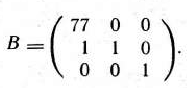
Теперь находим матрицу
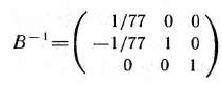
и определяем векторы
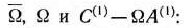
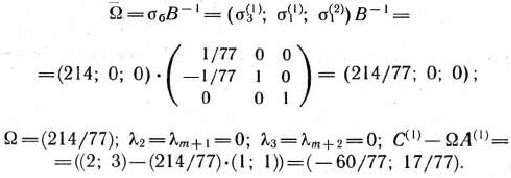
Подзадача I имеет вид
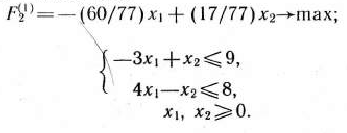
Оптимальным планом последней задачи является
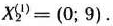
Так как
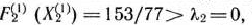
то рассматриваемый базис определяет опорный план главной задачи, не являющийся оптимальным.
Вторая большая итерация.
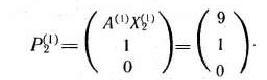
Соответственно
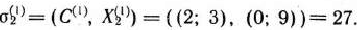
Чтобы определить вектор, исключаемый из базиса, разложим векторы 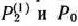 по векторам рассматриваемого базиса, т.е.
по векторам рассматриваемого базиса, т.е.
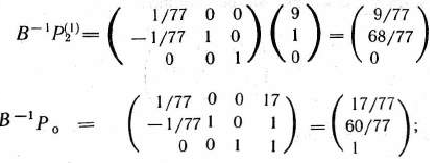
и найдем min (17/77:9/77; 60/77:68/77)= min (17/9; 15/17) = = 15/17. Следовательно, из базиса исключаем второй вектор, т. е. вектор Новый базис образуют векторы
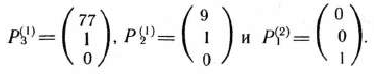
Матрица, составленная из компонент этих векторов, такова:
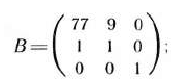
обратная к ней имеет вид
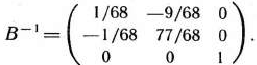
Находим векторы
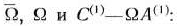
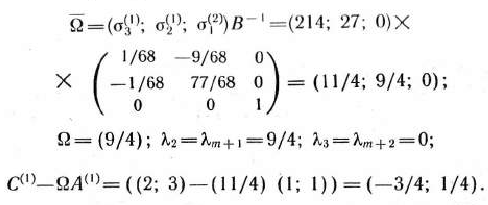
Составляем и решаем подзадачу 1:
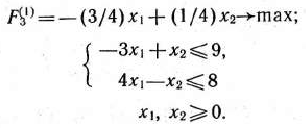
Подзадача 1 имеет оптимальный план
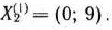
При этом

Составляем и решаем подзадачу 2:
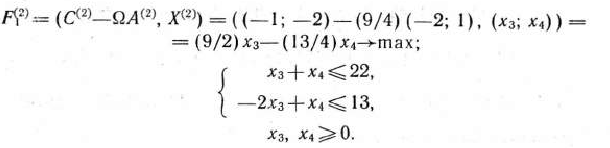
Подзадача 2 имеет оптимальный план
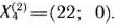
Так как
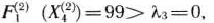
то рассматриваемый базис определяет опорный план главной задачи, не являющийся оптимальным.
Третья большая итерация. Из чисел
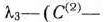
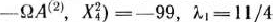
наименьшее отрицательное есть —99. Поэтому в базис вводим вектор
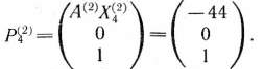
Соответственно
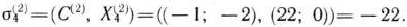
Чтобы определить вектор, выводимый из базиса, разложим векторы 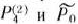 по векторам рассматриваемого базиса, т. е.
по векторам рассматриваемого базиса, т. е.
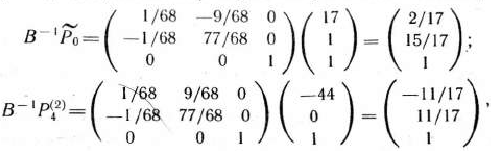
и найдем min (15/17:11/17; 1/1)= 1. Таким образом, из базиса исключаем вектор 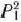 . Новый базис образуют векторы
. Новый базис образуют векторы
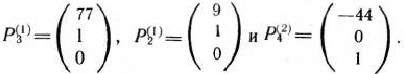
Матрица, обратная матрице, составленной из компонент векторов 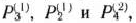 , такова:
, такова:
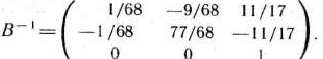
Найдем векторы
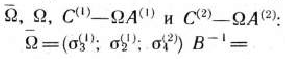
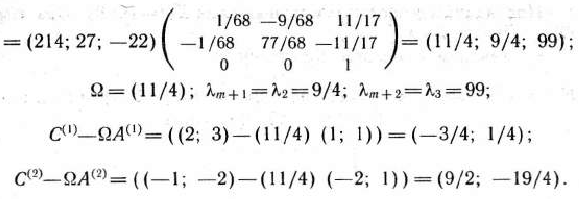
Составляем и решаем подзадачу I:
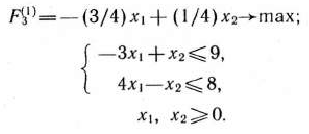
Оптимальный план
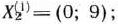
при этом
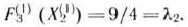
Составляем и решаем подзадачу 2:
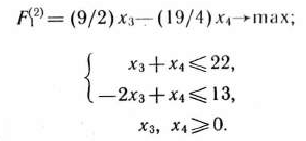
Подзадача 2 имеет оптимальный план
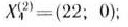
при этом
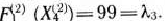
Таким образом, определяемый рассматриваемым базисом опорный план является оптимальным. Для его нахождения разложим вектор 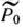 по векторам данного базиса:
по векторам данного базиса:
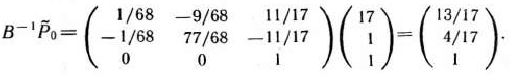
Значит, в оптимальном плане главной задачи отличные от нуля компоненты таковы:
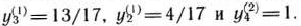
Используя формулы (124) и (125), находим оптимальный план исходной задачи (135)—(137):
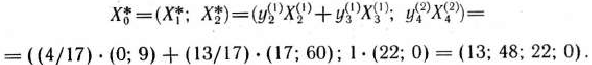
Максимальное значение целевой функции
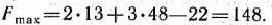
В заключение отметим, что помимо метода Данцига—Вулфа существуют и другие методы, позволяющие сводить решение задачи большой размерности к решению ряда подзадач меньшей размерности.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
