Оглавление:




Поверхности вращения, конические поверхности
- Поворотная поверхность, конус поверхность 1. Поворотная поверхность Поверхность, образованная вращением плоской кривой вокруг оси в плоскости, называется вращающейся поверхностью. Предположим, кривая L находится на плоскости Oyz. Уравнение для этой кривой можно записать в виде: jF («; *) = O, \ х = 0 Найти уравнение поверхности, образованное вращением кривой L вокруг оси Oz. Возьмем любую точку M (x; y; z) на поверхности.
Координаты точки N обозначены (0; yi; 2i). Сегменты OiM и 0 \ N имеют одинаковый радиус окружности. Итак, 01M = Q \ N. Но 01 A / = y / x2 + y2, OxN = |? / Я | Поэтому | i / i | = yjx1 + y2 или y 1 = ± \ / x2 + y1. Кроме того, z \ = 2;. Понятно что.
Нарисуйте точку, перпендикулярную оси Oz через точку M, и укажите пересечение с осью Oz и кривой L через 0 \ и N соответственно. Людмила Фирмаль
• Поскольку точка N находится на кривой L, ее координаты удовлетворяют уравнению (1). Следовательно, F (y \ z ) = 0. Исключая вспомогательные координаты yi и z \ точки N, получаем уравнение. F (± y / x * + y *] ‘z) = 0. (2) Уравнение (2) является предпочтительным уравнением для вращающейся поверхности и удовлетворяется координатами любой точки M на этой поверхности, а не координатами точек, не находящихся на вращающейся поверхности.
Как видите, уравнение (2) можно получить из (1), просто заменив y на ± y / x2 4-2 / 2, и координата 2 сохраняется. Очевидно, что если кривая (1) вращается вокруг оси Oy, уравнение плоскости вращения имеет вид F («; ± vV + ^) = 0; Если кривая находится в плоскости Oxu (z = 0) и ее уравнение F (x \ y) = 0, уравнение плоскости вращения, образованное вращением кривой вокруг оси Ox, имеет вид F (x; ± у / у2 + z2 ) = 0
| Прямая и плоскость в пространстве. Основные задачи | Канонические уравнения поверхностей второго порядка |
| Цилиндрические поверхности | Понятие множества. Логические символы |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Пример: поверните линию 2 / = .g вокруг оси Oz. Результирующая поверхность (ее формула ± y / x2 4-y2 = z или x2 4-y2 = <r2) называется вторичным конусом. 2. Коническая поверхность Поверхность, образованная прямой линией, которая проходит через определенную точку P и пересекает определенную плоскую линию L (не через P), называется конической поверхностью или конусом. Кроме того, линия L называется конической направляющей, точка P — ее вершина, а прямая линия, описывающая поверхность, называется генератором.
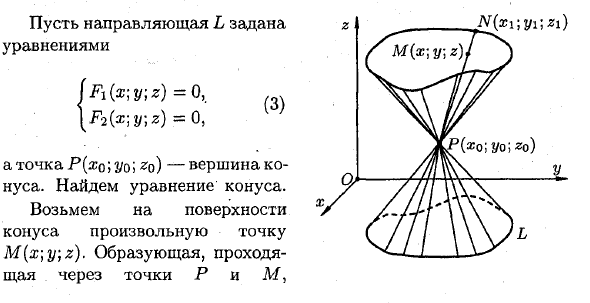
Точка P (x0 \ y0 \ z0) является вершиной конуса. Найти уравнение коники. Возьмем любую точку M (x \ y; z) на поверхности конуса. Генератор, проходящий через точки P и M,Пересекает направляющую L в определенной точке N (x \ yi \ z ). Координаты точки N удовлетворяют направляющему уравнению (3). f * i (si; i / r, *. i) = о, {F2 (xl] yl-z1) = 0. Каноническое уравнение генератора, проходящего через точки P и iV, имеет вид x-x0 y-y o z-Zq Xi-x0 yi- y0 Zi-z0 Удаление a; i, yi и z \ из уравнений (4) и (5) приводит к уравнению конической поверхности, связанному с текущими координатами x, y и z.
Дайте руководство L как уравнение («;»; *) = 0, () \ F2 (x] y; z) = O ,; Людмила Фирмаль
Пример: создание уравнения конуса с вершинами в вершинах 2 2 0 (0; 0; 0), если направляющая является эллипсом ^ + pg == 1> в плоскости z-c. ♦ M (x \ y \ z) — любая точка на конусе. Генератор канонических уравнений, проходящий через точку (0; 0; 0) и точку (xi \ yi \ z ) Пересечение генеалогии ОМ и эллипса — = = -. IS- Xi y 1 Z \ включают y \ и Zi из этих уравнений и уравнений 2 2 Вл / ли ^ 2-б ^ -1 (б) (Точка (xiji / i; zi) находится на эллипсе), 2i = c. Есть: == Следовательно, o: i = с • -и j / i = ii и j /! Значение присваивается. в Эллиптическое уравнение (6),
