Оглавление:
Разложение функций в ряд Тейлора (Маклорена) находит широкое практическое применение в вопросах приближенного вычисления значений функций, определенных интегралов (в тех случаях, когда первообразная нс выражается через элементарные функции или находится сложно), приближенного решения дифференциальных уравнений. Обратимся к примерам подобного практического применения.
Пусть требуется вычислить значение функции 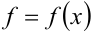 при
при 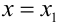 с заданной точностью. Если функцию
с заданной точностью. Если функцию 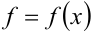 в интервале
в интервале 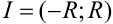 можно разложить в степенной ряд
можно разложить в степенной ряд 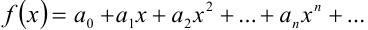 , и
, и 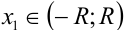 , то точное значение
, то точное значение 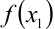 равно сумме этого ряда при
равно сумме этого ряда при 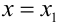 , т.е.
, т.е. 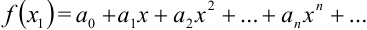 , а приближённое — частичной сумме
, а приближённое — частичной сумме 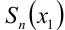 , т.е.
, т.е. 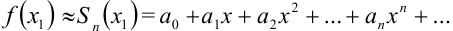 . Точность этого равенства увеличивается с ростом
. Точность этого равенства увеличивается с ростом 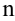 .
.
Пример №36.6.
Найдите приближенное значение выражения 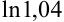 с точностью до 0,0001, используя известные разложения функций в ряд Маклорена.
с точностью до 0,0001, используя известные разложения функций в ряд Маклорена.
Решение:
Воспользуемся известным разложением в ряд Маклорена функции 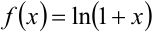 :
: 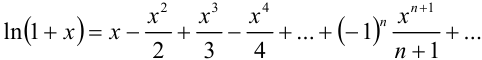 Поскольку
Поскольку 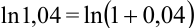 , подставим в данное разложение вместо
, подставим в данное разложение вместо 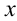 0,04, получим
0,04, получим 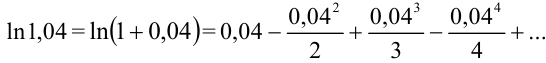 Так как мы имеем знакочередующийся ряд, то при замене его суммы некоторой частичной суммой абсолютная погрешность нс превышает модуля первого отброшенного члена. Непосредственной проверкой убеждаемся, что
Так как мы имеем знакочередующийся ряд, то при замене его суммы некоторой частичной суммой абсолютная погрешность нс превышает модуля первого отброшенного члена. Непосредственной проверкой убеждаемся, что 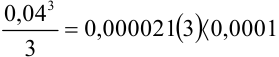 , следовательно, достаточно ограничиться двумя первыми членами разложения:
, следовательно, достаточно ограничиться двумя первыми членами разложения: 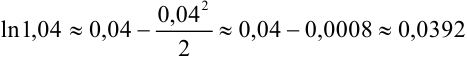 .
.
Ответ: 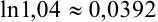 .
.
Пусть требуется вычислить 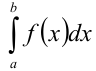 с определённой точностью. Если подынтегральную функцию
с определённой точностью. Если подынтегральную функцию 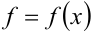 можно разложить в ряд по степеням
можно разложить в ряд по степеням 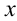 , и интервал сходимости
, и интервал сходимости 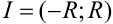 включает в себя отрезок
включает в себя отрезок 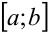 , то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда (свойство 4 лекции 35).
, то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда (свойство 4 лекции 35).
Пример №36.7.
Вычислить интеграл 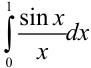 с точностью до 0,0001, где при
с точностью до 0,0001, где при 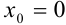 значение подынтегральной функции принимается равным 1.
значение подынтегральной функции принимается равным 1.
Решение:
Подынтегральная функция 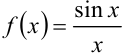 представляет собой частное
представляет собой частное 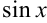 и
и 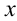 , поэтому для её разложения в ряд Маклорена воспользуемся разложением функции
, поэтому для её разложения в ряд Маклорена воспользуемся разложением функции 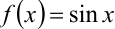 :
: 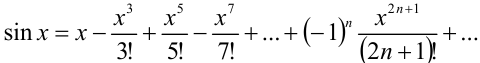 Поделим обе части этого разложения на
Поделим обе части этого разложения на 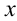 :
:
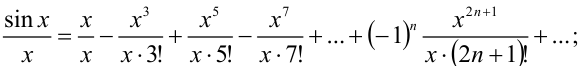
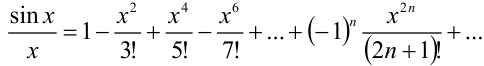
Это разложение имеет место на всей числовой оси, поэтому его можно почленно интегрировать на [0;1]:
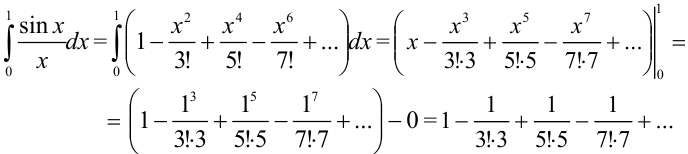
Полученный ряд является знакочередующимся рядом. Так как 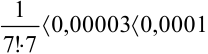 , то достаточно взять три первых члена разложения:
, то достаточно взять три первых члена разложения: 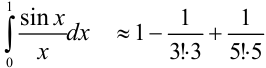 .
.
Вычисляя промежуточные результаты с пятью десятичными знаками, получим окончательный результат с четырьмя верными десятичными знаками: 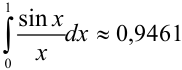 .
.
Ответ: 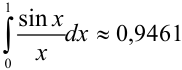 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Ряды Тейлора и Маклорена. |
| Разложение элементарных функций в ряд. |
| Тригонометрический ряд Фурье. |
| Разложение в ряд Фурье периодических функций с периодом 2п. |
