Правило Лопиталя
В э том параграфе мы докажем утверждение, которое может оказаться полезным при вычислении пределов функций, которые приводят к неопределенностям вида 2 или
Теорема. Пусть функции 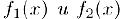 определены и дифференцируемы в некотором интервале, содержащем точку
определены и дифференцируемы в некотором интервале, содержащем точку 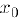 , кроме, может быть, самой этой точки, и
, кроме, может быть, самой этой точки, и 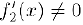 в этом интервале. Предположим также, что
в этом интервале. Предположим также, что
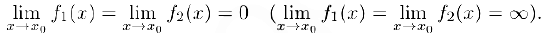
Тогда, если существует предел (конечный или бесконечный)
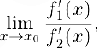
то существует также предел
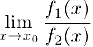
и
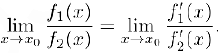
(правило Лопиталя)
Доказательство проведем для неопределенности  . Доопределим функции
. Доопределим функции в точке
в точке 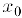 нулевыми значениями и применим теорему Коши к отрезку
нулевыми значениями и применим теорему Коши к отрезку 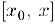 :
:
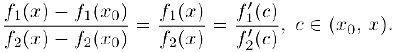
Из последнего равенства и следует утверждение теоремы, так как при 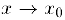 также и
также и 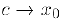 .
.
Замечание 1. Правило Лопиталя сохраняет также свою силу и в случае неопределенностей вида 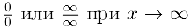 .
.
Замечание 2. В некоторых случаях правило Лопиталя целесообразно применять повторно. При нахожденш! сложных пределов имеет смысл комбинировать свойства пределов (глава IV’. §4, пункты 2 — 4) и правило Лопиталя.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Математический анализ онлайн помощь
Возможно эти страницы вам будут полезны:
