Оглавление:
С понятием последовательности вы ознакомились ещё в основной школе, когда изучали арифметическую и геометрическую прогрессии. Несколько последовательностей:
1) бесконечная последовательность рациональных приближений числа 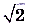 с точностью до десятых, сотых, тысячных и т. д.:
с точностью до десятых, сотых, тысячных и т. д.:
1,4; 1,41; 1,414; 1,4142; 1,41421;… ; (*)
2) последовательность степеней с основанием 3, показателями которых являются рациональные приближения числа 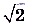 с точностью до десятых, сотых, тысячных и т. д.:
с точностью до десятых, сотых, тысячных и т. д.:
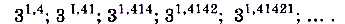
Числовой последовательностью называется функция 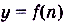 , которая задана на множестве натуральных чисел. При таком задании
, которая задана на множестве натуральных чисел. При таком задании 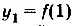 ,
, 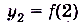 ,
, 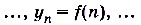 — соответственно первый, второй, n-й,… члены числовой последовательности.
— соответственно первый, второй, n-й,… члены числовой последовательности.
Обозначают числовые последовательности 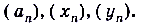 Числовые последовательности задают описательно, перечнем членов, либо с помощью формулы (n-го члена или рекуррентной).
Числовые последовательности задают описательно, перечнем членов, либо с помощью формулы (n-го члена или рекуррентной).
Например:
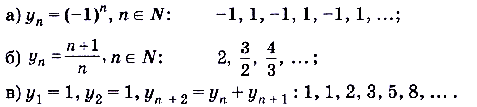
В курсе геометрии, чтобы вывести формулы длины окружности и площади круга, рассматривают последовательности вписанных в круг и описанных вокруг круга многоугольников. При этом отмечают, что при неограниченном увеличении числа сторон многоугольника его периметр всё ближе и ближе приближается к длине окружности (рис. 41).
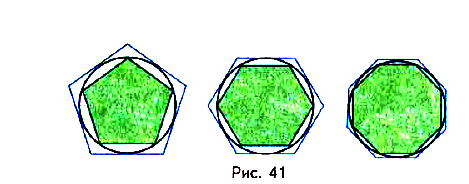
Так получают первое интуитивное понятие предела числовой последовательности. В курсе математического анализа — это одно из важнейших понятий. Рассмотрим его подробнее.
Пусть задано числовую последовательность 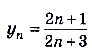 . Вычислим её первые пять членов и изобразим их на координатной прямой (рис. 42). Имеем:
. Вычислим её первые пять членов и изобразим их на координатной прямой (рис. 42). Имеем:
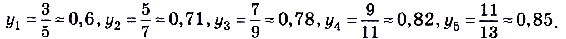
Как видим, с увеличением номера члена последовательности сами члены последовательности всё ближе и ближе приближаются к числу 1. Поскольку расстоянием между точками, которые соответствуют числам на координатной прямой, есть модуль разности этих чисел, то можно утверждать, что для данной последовательности 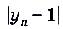
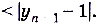
Очевидно, что при росте числа п члены заданной последовательности всё меньше и меньше будут отличаться от числа 1. Например: 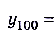
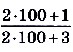
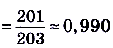 ,а
,а 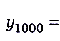
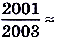
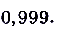
В данном случае для любого достаточно малого числа 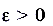 (эпсилон) можно найти такое число N (номер члена последовательности), что для всех последующих членов этой последовательности будет выполняться неравенство
(эпсилон) можно найти такое число N (номер члена последовательности), что для всех последующих членов этой последовательности будет выполняться неравенство 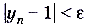 .
.
Например, в рассмотренной выше последовательности для 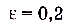 таким членом будет
таким членом будет 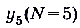 , поскольку
, поскольку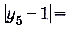
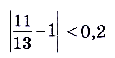 , а для
, а для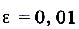 таким членом будет
таким членом будет 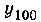 (проверьте).
(проверьте).
В этом случае говорят, что число 1 является пределом заданной числовой последовательности.
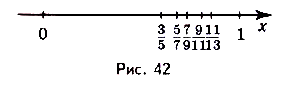
Число А называют пределом числовой последовательности 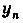 , если для любого
, если для любого 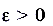 существует номер члена последовательности такой, что для всех
существует номер члена последовательности такой, что для всех 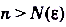 выполяется неравенство
выполяется неравенство 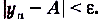
Обозначают: 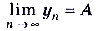 . Читают: предел числовой последовательности
. Читают: предел числовой последовательности 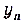 при n, стремящемся к бесконечности, равен А.
при n, стремящемся к бесконечности, равен А.
Пример №1
Вычислите предел последовательности 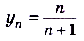 .
.
Решение:
Запишем несколько членов заданной последовательности: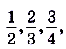
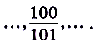 Как видим, ее члены стремятся к числу 1. Проверим наше предположение. По определению предела надо найти такое число N, что для всех
Как видим, ее члены стремятся к числу 1. Проверим наше предположение. По определению предела надо найти такое число N, что для всех 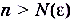 будет выполняться неравенство
будет выполняться неравенство 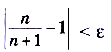 . Имеем:
. Имеем:
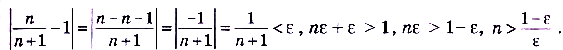
Следовательно, такое число существует. Например, при 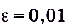 последнее неравенство будет иметь вид
последнее неравенство будет иметь вид 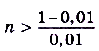 , или
, или 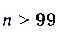 .
.
То есть, начиная с 100-го члена последовательности расстояние между любым членом последовательности и числом 1 будет меньше 0,01.
Следовательно, 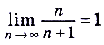 .
.
Докажите самостоятельно и запомните, что 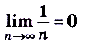 .
.
Если числовая последовательность 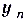 имеет предел, то она называется сходящейся. Если числовая последовательность предела не имеет, то она называется расходящейся.
имеет предел, то она называется сходящейся. Если числовая последовательность предела не имеет, то она называется расходящейся.
Рассмотрим свойства сходящихся последовательностей.
- Если последовательность имеет предел, то этот предел единственный.
- Предел постоянной последовательности равен значению любого члена этой последовательности, то есть
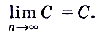
3. Предел суммы (разности) двух сходящихся последовательностей равен сумме (разности) пределов этих последовательностей , то есть:
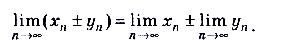
4. Предел произведения двух сходящихся последовательностей равен произведению пределов этих последовательностей , т.е.
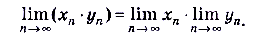
5.Если последовательности 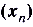 и
и 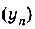 — сходящиеся ,
— сходящиеся , 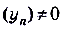 .
.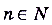 , то числовая последовательность
, то числовая последовательность 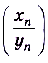 тоже сходящаяся и выполняется равенство
тоже сходящаяся и выполняется равенство
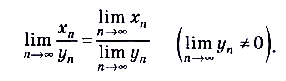
Пример №2
Найдите предел последовательности 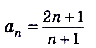 .
.
Решение:
Эту последовательность можно представить в виде суммы двух сходящихся последовательностей 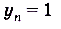 ,
,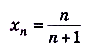 (проверьте). На основании свойств 2 и 3 имеем:
(проверьте). На основании свойств 2 и 3 имеем:
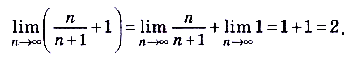
Для вычисления предела последовательности, которая задается как отношение двух многочленов 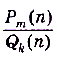 , используют следующее правило.
, используют следующее правило.
Для того чтобы вычислить предел числовой последователь кости, которая задаётся как отношение двух многочленов 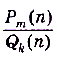 (одной переменной n, степеней m и k соответственно),каждый из которых имеет предел, равный бесконечности, необходимо каждый член заданных многочленов разделить на наивысшую степень п и выяснить, к чему стремится каждый из полученных членов заданного отношения.
(одной переменной n, степеней m и k соответственно),каждый из которых имеет предел, равный бесконечности, необходимо каждый член заданных многочленов разделить на наивысшую степень п и выяснить, к чему стремится каждый из полученных членов заданного отношения.
Пример №3
Вычислите 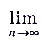
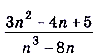 .
.
Решение:
Здесь 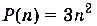
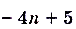 ,
, 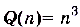
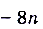 . Предел каждого многочлена равен бесконечности. Поскольку
. Предел каждого многочлена равен бесконечности. Поскольку  ,
, 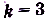 , то делим каждый член многочленов на
, то делим каждый член многочленов на 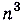 и выясняем, к чему стремится каждый из полученных членов.
и выясняем, к чему стремится каждый из полученных членов.
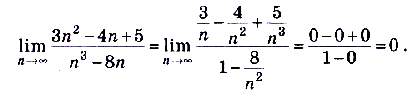
Пример №4
Вычислите:
a) 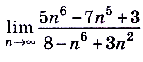 ; б)
; б) 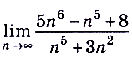 .
.
Решение:
a) 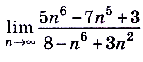
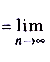
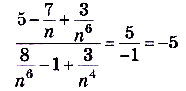
б) 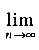
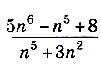
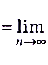
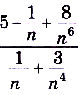
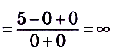 .
.
Заметим, что здесь не происходит деление на ноль, поскольку знаменатель лишь стремится к нулю, но ему не равен.
Проанализируем полученные ответы. В примере 3 степень числителя меньше степени знаменателя. Это означает, что знаменатель стремится к бесконечности быстрее, чем числитель, а следовательно, предел их отношения будет равняться нулю. В примере 4, в задании а) степени числителя и знаменателя одинаковы и в результате получили отношение коэффициентов при старших степенях. В задании б) степень числителя больше степени знаменателя. Это означает, что числитель стремится к бесконечности быстрее, чем знаменатель, а потому предел их отношения равен бесконечности. Итак, имеем еще такое правило.
Для того чтобы вычислить предел числовой последовательности при 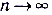 , которая задаётся как отношение двух многочленов
, которая задаётся как отношение двух многочленов 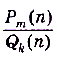 (одной переменной n, степеней m и k соответственно)* каждый из которых имеет предел,равный бесконечности, необходимо сравнить эти степени. Если:
(одной переменной n, степеней m и k соответственно)* каждый из которых имеет предел,равный бесконечности, необходимо сравнить эти степени. Если:
1 )m = k, то предел равен отношению коэффициентов при старших степенях заданных многочленов;
2) m < k , то предел равен нулю;
3) m> k, то предел равен бесконечности.
Пример №5
Пользуясь определением предела числовой последовательности, докажите, что 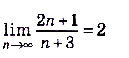 .
.
Решение:
Нужно доказать, что существует такое 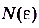 , что для всех
, что для всех 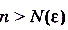 выполняется неравенство
выполняется неравенство 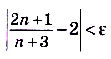 . Преобразуем выражение , стоящее в левой части :
. Преобразуем выражение , стоящее в левой части :
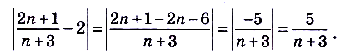
Пусть 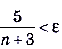 , тогда
, тогда 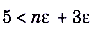 , а
, а 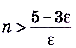 . Для любого
. Для любого 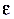 можем найти соответствующее
можем найти соответствующее 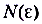 , например
, например 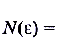
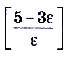 .
.
Итак, пределом заданной последовательности является число 2.
Пример №6
Вычислите: а) 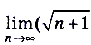
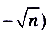 ; б)
; б) 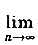
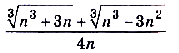 .
.
Решение:
а) Умножим и разделим выражение, стоящее под знаком предела, на сопряжённое.
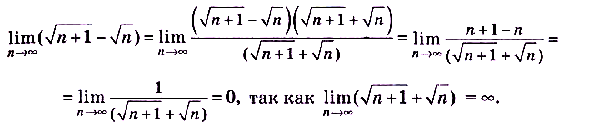
б) Разделим числитель и знаменатель дроби на n. Имеем:
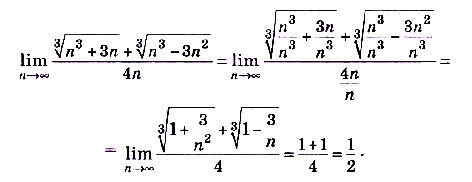
Предел и непрерывность функции
Часто говорят о значении функции в точке, пределе функции в точке, приращении функции в точке, непрерывности функции в точке. О каких точках идёт речь? О точках оси абсцисс — значениях аргумента.
Значение функции в точке
Пусть задано, например, функцию 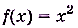
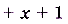 . Если х = 1, то соответствующее значение функции равно 3. Говорят, что в точке х = 1 значение функции f(x) равно 3. В точке х = 0 её значение равно 1, в точке х = 10 значение функции f(x) равно 111. Пишут:
. Если х = 1, то соответствующее значение функции равно 3. Говорят, что в точке х = 1 значение функции f(x) равно 3. В точке х = 0 её значение равно 1, в точке х = 10 значение функции f(x) равно 111. Пишут: 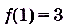 , f(0) =1 , f(10)=111.
, f(0) =1 , f(10)=111.
Предел функции в точке
Рассмотрим ту же функцию 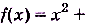
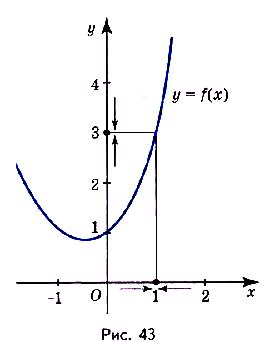
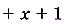 . Если значения её аргумента х достаточно близко и с обеих сторон приближаются к 1, то соответствующие значения функции как угодно близко приближаются к числу 3 (рис. 43). Об этом свидетельствуют данные таблицы (рис. 44), в которой содержатся значения.
. Если значения её аргумента х достаточно близко и с обеих сторон приближаются к 1, то соответствующие значения функции как угодно близко приближаются к числу 3 (рис. 43). Об этом свидетельствуют данные таблицы (рис. 44), в которой содержатся значения.

функции 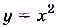
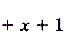 для 10 значений аргумента, близких к числу 1, и график, изображённый на рисунке 43.
для 10 значений аргумента, близких к числу 1, и график, изображённый на рисунке 43.
Другими словами: разность 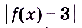 может стать и оставаться сколь угодно малой, если разность
может стать и оставаться сколь угодно малой, если разность 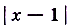 будет достаточно малой. В этом случае говорят, что предел функции f(x) в точке х = 1 равен 3. Пишут: если х —> 1, то
будет достаточно малой. В этом случае говорят, что предел функции f(x) в точке х = 1 равен 3. Пишут: если х —> 1, то 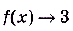 , или
, или 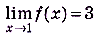 .
.
Существенная деталь: функция может иметь предел даже в такой точке, в которой она не определена, потому что знаменатель не может равняться нулю. Во всех остальных точках функция 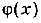 имеет такие же значения, как и функция f(x), ибо
имеет такие же значения, как и функция f(x), ибо 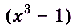 :
: 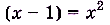
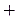
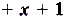 , если
, если 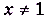 . График функции
. График функции 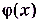 изображён на (рис) 45.
изображён на (рис) 45.
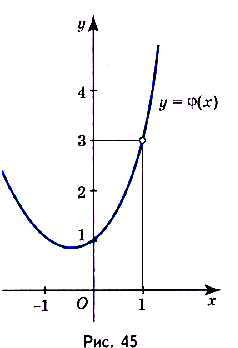
Хотя значение функции 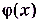 в точке x= 1 не существует, а её предел в этой точке существует и равен 3.
в точке x= 1 не существует, а её предел в этой точке существует и равен 3.
Определение предела функции можно сформулировать так.
Число b называется пределом функции f(x)в точке 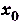 ,если для любого положительного числа
,если для любого положительного числа 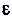 можно указать такое положительное число
можно указать такое положительное число 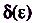 , что для всех значений х из промежутка
, что для всех значений х из промежутка 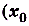
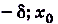
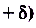 кроме, возможно, самой точки
кроме, возможно, самой точки 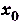 , справедливо неравенство
, справедливо неравенство 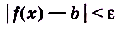 .
.
Пишут так: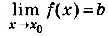 .
.
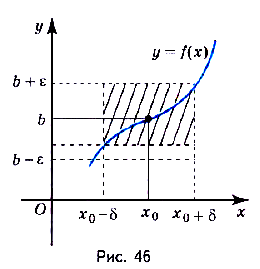
Определение предела функции имеет простое геометрическое толкование: какое бы ни было достаточно малое наперёд за-данное положительное число (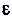 ), можно указать такое положительное число
), можно указать такое положительное число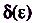 , что для всех точек х, которые удалены от точки
, что для всех точек х, которые удалены от точки 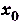 не далее чем на
не далее чем на 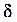 , график функции
, график функции 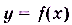 лежит внутри полосы — шириной
лежит внутри полосы — шириной 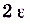 , ограниченной прямыми
, ограниченной прямыми 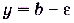 и
и 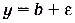 (рис. 46).
(рис. 46).
Предел функции имеет интересные свойства. Например:
• функция не может иметь двух различных пределов в точке;
• если с — число, то 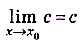 ;
;
Несколько свойств сформулируем в виде теоремы.
Теорема. Если каждая из функций f(x) и g(x) имеет предел в точке 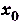 , то в этой точке существуют пределы функций
, то в этой точке существуют пределы функций 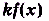 ,
,
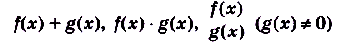
справедливы равенства:
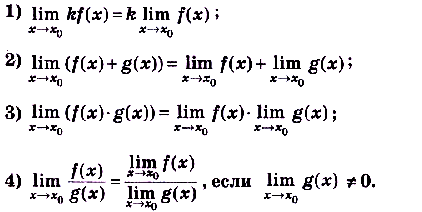
Другими словами можно сказать так.
Постоянный множитель можно выносить за знак предела. Предел суммы (разности, произведения) функций равен сумме (разности, произведению) пределов данных функций. Предел отношения двух функций равен отношению их пределов, если предел делителя не равен нулю.
Эти свойства используют для вычисления пределов функций в заданных точках.
Пример №7
При условии, что 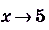 вычислите предел функции f(x), если:
вычислите предел функции f(x), если:
а)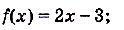 б)
б)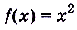
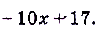
Решение:
a) 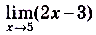
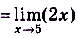
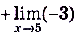
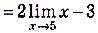
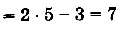 ;
;
б) 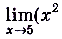
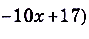
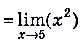
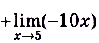
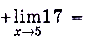
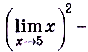
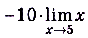
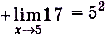
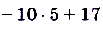
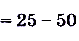
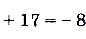 .
.
Замечание. Решая такие упражнения, некоторые преобразования можно выполнять устно.
В предыдущих примерах для нахождения предела достаточно было подставить в данное выражение предельное значение аргумента. Но часто такая подстановка приводит к неопределённости вида 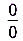 ,
, 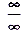 ,
,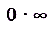 ,
,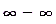 ,
, 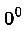 ,
, 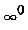 ,
, 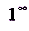 . В таких случаях и сначала необходимо преобразовать данное выражение, а уже потом вычислять предел. Нахождение предела таким образом называется раскрытием неопределённостей.
. В таких случаях и сначала необходимо преобразовать данное выражение, а уже потом вычислять предел. Нахождение предела таким образом называется раскрытием неопределённостей.
Пример №8
Найдите 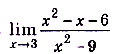 .
.
Решение:
Поскольку при 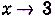 предел знаменателя равен нулю, то использовать теорему о пределе частного нельзя. Непосредственная подстановка в данное выражение предельного значения аргумента х = 3 приводит к неопределенности вида —
предел знаменателя равен нулю, то использовать теорему о пределе частного нельзя. Непосредственная подстановка в данное выражение предельного значения аргумента х = 3 приводит к неопределенности вида — 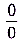 .
.
Чтобы её раскрыть, разложим числитель и знаменатель дроби на множители. Имеем:
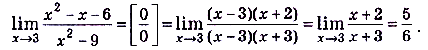
Приращения аргумента и функции
Пусть дано, например, функцию 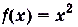 . В точке
. В точке 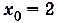 ее значение
ее значение 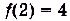 . Увеличим значение аргумента на 0,01, то есть, пусть
. Увеличим значение аргумента на 0,01, то есть, пусть 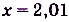 . Соответствующее значение функции
. Соответствующее значение функции 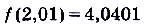 . По сравнению с предыдущим значением оно увеличилось на 0,0401. Здесь 0,01 — приращение аргумента, а 0,0401 — соответствующее приращение функции, а именно: приращение функции
. По сравнению с предыдущим значением оно увеличилось на 0,0401. Здесь 0,01 — приращение аргумента, а 0,0401 — соответствующее приращение функции, а именно: приращение функции 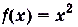 на промежутке [2; 2,01].
на промежутке [2; 2,01].
Приращением аргумента в точке 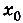 называют разность
называют разность 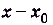 , где х — произвольное число, которое мало отличается от
, где х — произвольное число, которое мало отличается от 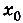 и может быть положительным или отрицательным. Соответствующее приращение функции f(x) — разность
и может быть положительным или отрицательным. Соответствующее приращение функции f(x) — разность 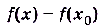 .
.
Приращение аргумента х обозначают символом 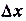 , а приращение функции
, а приращение функции 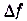 ,
, 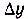 (читают: дельта икс, дельта эф, дельта игрек). Так, в рассматриваемом примере
(читают: дельта икс, дельта эф, дельта игрек). Так, в рассматриваемом примере 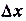 = 0,01,
= 0,01, 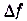 = 0,0401.
= 0,0401.
Геометрически приращение аргумента изображается приращением абсциссы точки кривой, а приращение функции — приращением ординаты этой точки (рис. 47),
Свойства этих понятий показано на рисунках 47 и 48. Если функция f(x) — возрастающая и 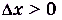 , то
, то 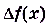 — число положительное, а если f(х) — убывающая функция и
— число положительное, а если f(х) — убывающая функция и 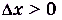 , то
, то 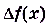 — число отрицательное.
— число отрицательное.
Непрерывность функции
Как связаны между собой приращения аргумента х и функции 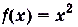 в точке
в точке 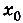 = 2? Если
= 2? Если 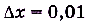 , то
, то 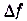 = 0,0401; если
= 0,0401; если 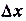 = 0,001, то
= 0,001, то 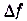 = 0,004001 и т. д. Вообще, если
= 0,004001 и т. д. Вообще, если 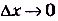 , то и
, то и 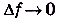 , т. е. приращение функции стремится к нулю, когда стремится к нулю приращение аргумента (слева или справа). В таком случае говорят, что функция f(x) непрерывна в точке
, т. е. приращение функции стремится к нулю, когда стремится к нулю приращение аргумента (слева или справа). В таком случае говорят, что функция f(x) непрерывна в точке 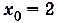 .
.
| Функция f(x) называется непрерывной в точке 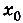 , если в этой точке достаточно малым приращениям аргумента соответствуют сколь угодно малые приращения функции.
, если в этой точке достаточно малым приращениям аргумента соответствуют сколь угодно малые приращения функции.
Иначе: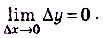
Преобразуем последнее равенство:
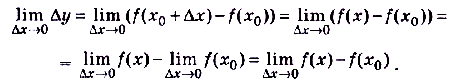
Поскольку 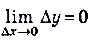
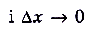 , когда
, когда 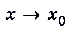 то получим
то получим 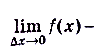
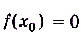 , отсюда
, отсюда
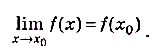
Функция у =f(x) называется непрерывной в точке 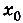 , если существует предел функции в этой точке и он равен значению функции в точке
, если существует предел функции в этой точке и он равен значению функции в точке 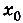 .
.
Использование последней формулы существенно упрощает вычисление пределов для непрерывных функций.
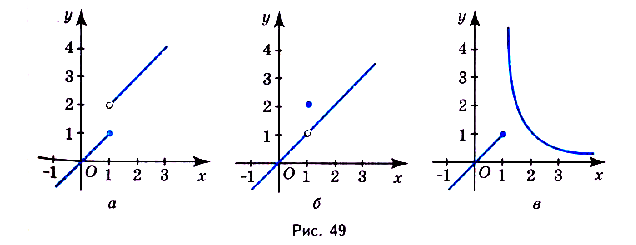
Функция называется непрерывной на промежутке, если она непрерывна в каждой его точке. График такой функции — непрерывная кривая (её можно провести, не отрывая карандаш от бумаги).
На рисунке 49 изображены графики функций, имеющих разрывы в точке х = 1; они не являются непрерывными в этой точке.
Непрерывными в каждой точке своей области определения есть элементарные функции — рациональные, тригонометрические, 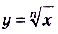
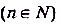 , а также функции, образованные из них с помощью четырёх арифметических действий. Графики элементарных функций на каждом промежутке из области определения являются неразрывными линиями.
, а также функции, образованные из них с помощью четырёх арифметических действий. Графики элементарных функций на каждом промежутке из области определения являются неразрывными линиями.
Теория пределов — большой и интересный раздел курса математического анализа, который изучается в университетах. В школе этот материал изучают обзорно, на основе наглядных представлений и интуиции. Представление о пределах и их свойствах желательно иметь для изучения производной и её применений — мощного аппарата для исследования многих реальных процессов.
Предлагаем вам ознакомиться с одним из интересных и важных фактов теории пределов. Рассмотрите таблицу, составленную с помощью Excel.
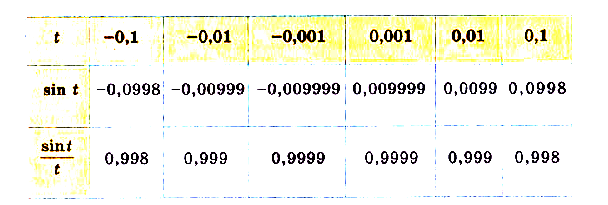
Как видим, при достаточно малых значениях 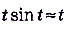 , а
, а 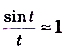 .
.
В курсе математического анализа строго доказывается, что
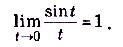
Это равенство называется первым замечательным пределом. Его используют для нахождения пределов функций, связанных с тригонометрическими.
Пример №9
Вычислите предел 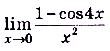 .
.
Решение:
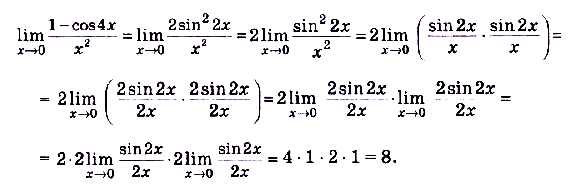
Пример №10
Вычислите:
а) 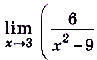
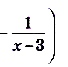 б)
б) 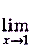
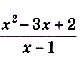 в)
в) 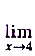
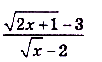
Решение:
а) В точке x = 3 предел каждой из дробей не существует, поэтому воспользоваться теоремами о пределах мы не можем. Упростим функцию, содержащуюся под знаком предела, выполнив действие вычитания. Имеем:
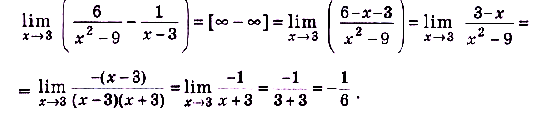
б) В тючке х = 1 данная функция не определена, но дробь 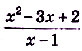 можно сократить:
можно сократить: 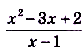
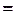
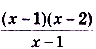
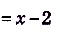 .
.
Поскольку для вычисления предела при 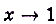 саму точку
саму точку 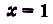 можно исключить и не рассматривать, то
можно исключить и не рассматривать, то
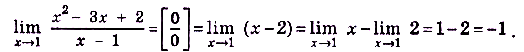
в) Умножим числитель и знаменатель дроби на выражения, сопряжённые к данным.
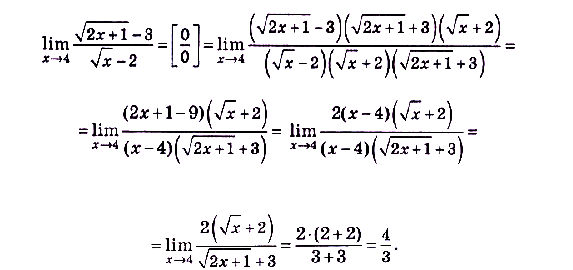
Пример №11
Найдите приращение функции 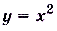 при переходе значения аргумента от 3 до 3,5.
при переходе значения аргумента от 3 до 3,5.
Решение:
Способ 1. Имеем 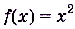 , a
, a 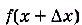
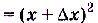 , тогда
, тогда
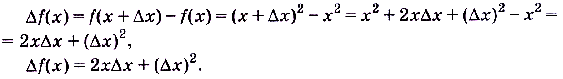
До этой формуле можно вычислить значение 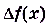 для любых х и
для любых х и 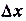 . В частности, в нашем примере х = 3,
. В частности, в нашем примере х = 3,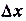 = 3,5 — 3 = 0,5, поэтому
= 3,5 — 3 = 0,5, поэтому 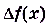
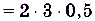
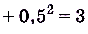
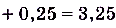 .
.
Способ 2. 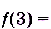
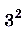 ,
,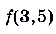
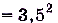 .
.
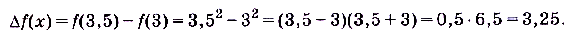
Пример №12
Для функции 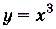 найдите:
найдите:
а) приращение функции при переходе от некоторой точки х к точке х + 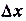 ;
;
б) предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Решение:
a) 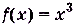 ,
, 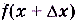
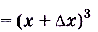 .
.
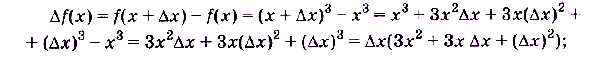
б) 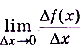
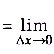
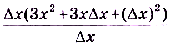
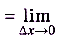
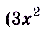
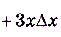
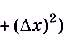
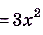 , поскольку
, поскольку 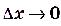 , а х — не зависит от
, а х — не зависит от 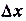 .
.
Вычисление пределов, производная функции, исследование функций
Пример №13
Вычислить предел 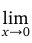
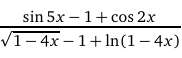 .
.
Решение:
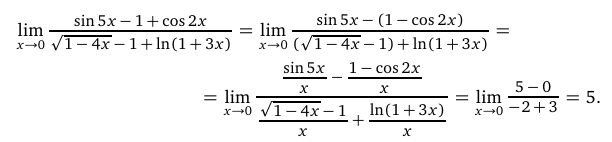
Таблица производных основных элементарных функций

Правила дифференцирования
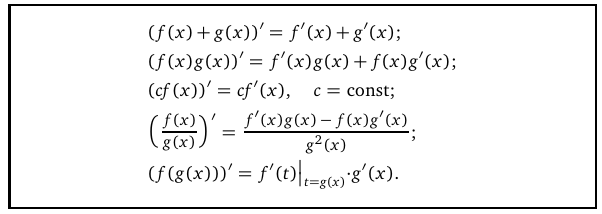
Пример №14
Вычислить производную функции у(х), заданной в неявной форме 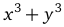
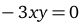 .
.
Решение:
В случае неявного задания функции F(x,y) = 0 для нахождения ее производной нужно:
1) вычислить производную по переменной х функции F(x, у(х)),
2) приравнять эту производную нулю,
3) решить полученное уравнение относительно у'(х). В нашем случае получаем 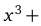
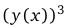
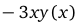
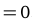 ,
,
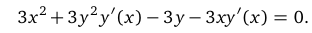
Отсюда получим, что 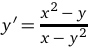 при
при 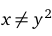 .
.
Пример №15
Провести исследование функции 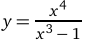
Решение:
1. Функция определена и непрерывна всюду, кроме точки х=1. Она равна нулю в точке х = 0.
2. Вычислим первую производную данной функции: 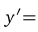
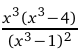 .
.
3. Нахождение интервалов монотонности и точек экстремума функции.
Приравнивая первую производную функции нулю, находим ее критические точки (с учетом тех точек, где производная не существует): 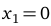 ,
, 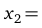
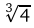 ,
, 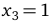 . Данные точки разбивают область определения функции на четыре промежутка монотонности:
. Данные точки разбивают область определения функции на четыре промежутка монотонности: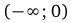 ,
, 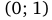 ,
, 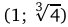 ,
, 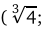
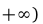 . Так как у’ >0 при
. Так как у’ >0 при 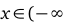
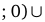
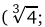
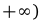 и у’ < 0 при
и у’ < 0 при 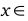
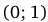
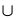
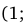
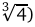 ,то на промежутках
,то на промежутках 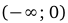 и
и 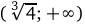 функция возрастает, а на промежутках (0; 1) и
функция возрастает, а на промежутках (0; 1) и 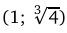 убывает. Точка х = 0 является точкой локального максимума
убывает. Точка х = 0 является точкой локального максимума 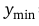
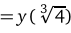
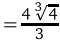 .
.
4. Найдем промежутки выпуклости и точки перегиба графика функции. Для этого исследуем знак второй производной:
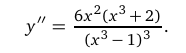
Так как у»>0 при 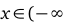 ;
; 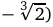
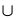
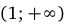 и у»<0 при
и у»<0 при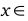
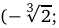
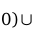
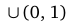 , то на промежутках
, то на промежутках 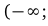
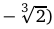 и
и 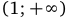 график функции является выпуклым вниз, а на промежутках
график функции является выпуклым вниз, а на промежутках 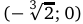 и (0, 1) график функции является выпуклым вверх. При этом точка
и (0, 1) график функции является выпуклым вверх. При этом точка 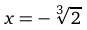 области определения функции, при переходе через которую вторая производная меняет знак, задает точку перегиба,
области определения функции, при переходе через которую вторая производная меняет знак, задает точку перегиба, 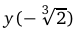
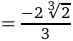 .
.
Точка х = 1 не задает точку перегиба, поскольку она не входит в область определения функции.
5. Найдем асимптоты графика.
Вертикальной асимптотой является прямая х= 1, поскольку
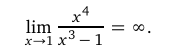
Найдем наклонные асимптоты графика функции 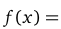
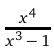 .
.
Уравнение наклонной асимптоты имеет вид 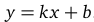 . Для определения ее параметров последовательно вычислим два предела:
. Для определения ее параметров последовательно вычислим два предела:
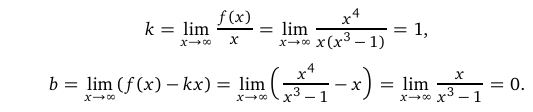
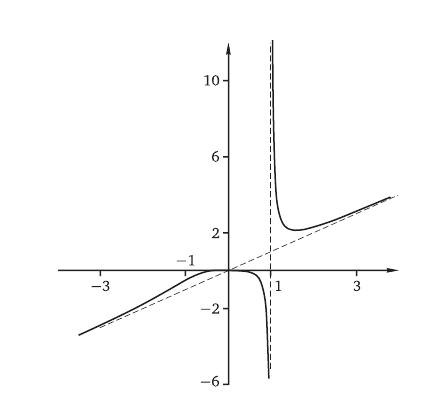
В результате получаем, что наклонной асимптотой является прямая у = х. Исследование функции закончено.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Первообразная и интеграл |
| Функции и их основные свойства |
| Степени с действительными показателями |
| Показательные функции |
