Оглавление:





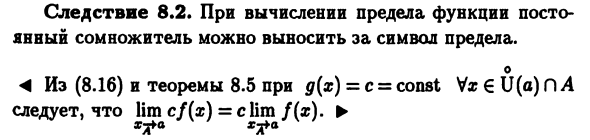




Пределы действительных функций
- Пусть X метрическое пространство, а X Предельная точка множества AS X. Функция J: A- * R принимает значение пространства R Реальное число Для таких функций вы можете ввести арифметические операции. Два стригущий лишай дан Функции} (x) и g (x) имеют значения R и обозначение f (x) ^ g (x) Означает, что неравенство верно Vx € A. И сумма f (x) + g (x) определяется как результат сложения Соответствующее значение функции. Определить также Функция вычитания, умножения и деления (последняя У рассматриваемой точки χe A есть этот делитель Точка не ноль).
Функция f (x) называется: 1)какие / (*)> 0 (f (x)> 0) VxeV (a) CiA (8,13) (Аналогичным образом определяют неположительную функцию (F (x) <0), отрицательное (f (x) <0) и не равно нулю 2) Ограничение как x-> if (сверху вниз) о 6 R постоянная и проколотая окрестность U (а) Относится к таким вещам , C> 0 (f (x) ^ c, f (x)> c) VxeV (a) DA; (8.14) 3) х-га бесконечно мала (см. (8.6)), если lim f (x) = 0; 4) x-g бесконечность (см. (8.7) — (8.9)), если lim / (x) = oo (= + oo или -oo). Из примера 8.1 ограничение на x-ga для функции / (x) Сохранение с x-> постоянным значением c = const равно c. Для функции со значением в R, main Ограничить теорему.
Когда x-m> a, неотрицательный (положительный) О л Панк Чад U (а) существует. Людмила Фирмаль
Читатель может доказать эти теоремы. Независимо от вышеуказанного определения, Свойство реальной абсолютной стоимости. Теорема 8.5. Функция f (x) с конечной x-ga Ограничено Теорема 8.6 (функция, ее пределы и Бесконечно маленький). Конечный предел функции f (x) равен 6 € R только если x-> и функция равна сумме Число 6 и бесконечно малые а (х) Теорема 8.7. Белые функции f (x) и g (x) имеют вид ^, А их сумма f (x) + g (x) и произведение f (x) g (x) Когда ограничено Теорема 8.8. Белые функций a (x) и 0 (x) бесконечны Если оно меньше x-a, a (x) + β (k) бесконечно мало
Теорема 8.0. Функция f (x) И а (х) бесконечно мал, как х-> а, и произведение f (x) a (x) бесконечно мал при x-> a. Необходимость 8.1. Два бесконечно малых произведения Функция при x-> a является бесконечной функцией Докажите предельную теорему на основе этих теорем Количество, продукт, коэффициент. Тот же подход Доказательство может быть выполнено с учетом характеристик Ограничения на фактические функции актуальных функций Переменная (см. 7.4 и 7.5).
- Теорема 8.10 (сумма, произведение и Private). Следующее утверждение верно: (3 Km f (x) = bx e R) L (3 Ud (x) = 62 € R) 3 bma (f (x) + g (x)) = 61 + 62; (8,15) 3Hin / (s) 0 (s) = 6i62; <По теореме 8.6 f (x) = 61 + a (x) и g (x) = 62 + β (s), где a (x) и / 3 (x) — x-fta бесконечно малые функции. тогда f (x) + g (x) = bi + 62 + a (x) + β (α) • Из теоремы 8.9 a (x) +0 (x) бесконечно мал для x-ga. На рассмотрении Для теоремы 8.6 это означает справедливость (8.15). Напишите, чтобы доказать (8.16) f (x) g (x) = * i62 + <* (x) b2 + P (x) bx + a (x) / 3 (x). Сумма трех последних сроков по этому праву Бесконечно по теорем 8.8 и 8.9 и последующим 8.1 Маленький как х-> ню. Согласно теореме 8.6 Правосудие (8.16). (8.5) показывает, что есть проколотая окрестность
Ах ах U (o) of a, например, Vs∈U (a) PA \ d (x) -b2 \ <| & 2 | / 2 или B2-M / 2 | 62 | / 2 и \ 1 / d (x) \ < <2 / | 6r |. Следовательно, функция l / d (x) Ниже приводится bi + ot (x) & i (bi + a (x) b% \ bi a (x) b2-f3 (x) b] flf (x) ^ 2 +) C’i3 ‘) & 2V b2 «^ (j \ X) 02 I 02 Второй член в правой части этого равенства Теоремы 8.8 и 8.9 бесконечно малы для x-ga. Согласно теореме 8.6 это означает справедливость (8.17). ► Ясно, что (8.15) и (8.16) могут быть расширены Любое конечное количество терминов и факторов. Необходимость 8.2. При расчете функциональных ограничений о <g (x) = c = const Vs € U (a) из АА (8.16) и теоремы 8.5 lim cf (x) = исправление клима) ► *** *** 20 *
Символ константы может быть взят из символа ограничения. Людмила Фирмаль
Объедините этот результат с (8.15), чтобы получить правило Рассчитать предел линейной комбинации функций: если V & = 1, т lim fk (x) = bk и Re Ck = const Белый 171171 lim Y * <* D (*) = Y) c * lim fk (x) = YW (8.18) Учитывая определение предела, Бесконечно большая функция, легко доказать Теорема. Теорема 8.11 (Об отношении бесконечно малого n Бесконечно большая функция). Вери (х) — x-ga инфинитезимальная функция и x-a} a (x) Φ0 f (x) = 1 / a (x) — £ -> a * как бесконечно большое и наоборот f (x) бесконечно большой, как x-> a, a (x) = 1 // (x) Бесконечно маленький
Теорема 8.12 (Относительно сохранения функцией символов Ограничения). Если x-> a, функция f (x) конечна Эта функция сохраняет знак с ненулевыми пределами, тогда x-ga Это ограничение. Очевидно, что f (x) a, если x-ga разница g (x) -f (x) неотрицательна (положительна) (См. (8.13).) Следствие 8.3. Для x-ga функции f (x) и d (x) Существует предел 6i и 62 соответственно, если b \ <62 f (x) 0 и Если lim f (x) = 6, вы можете сказать, в любом случае B> 0 вместо 6> 0. Теорема 8.14 (при приближении к пределу неравенства). x-ga f (x) <p (x), если они ограничены Неравенство сохраняется при переходе к функции, а затем к ограничению. lim / (x) <\ img (x). xrfa v ‘xrfa
Смотрите также:
| Понятие предела отображения | Признаки существования предела действительной функции |
| Некоторые свойства предела отображения | Непрерывность функции в точке |
