Преобразование произведения синусов и косинусов в сумму с примером решения

Преобразование произведения синусов и косинусов в сумму (разность):

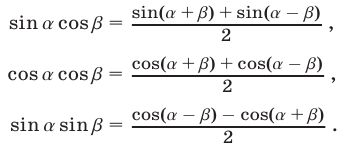
Выражение синуса и косинуса через тангенс половинного аргумента:

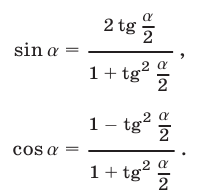
Пример №42.

Доказать тождества

Доказательство. 1) Преобразуем правую часть А первого равенства, пользуясь формулами (23) и (21). Так как

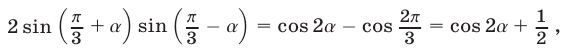
то

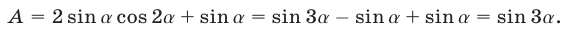
2) Аналогично преобразуется правая часть В второго равенства. Так как

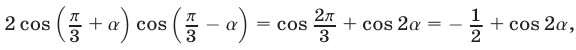
Замечание. Тождества примера 9 можно доказать, используя формулы (11) и (12). Из доказанных тождеств следует, что

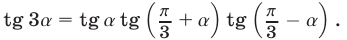
Пример №49.

Найти наибольшее и наименьшее значения выражения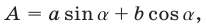 если по крайней мере одно из чисел a, b не равно нулю,

Решение:

Так как 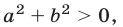то умножив и разделив данное выражение на 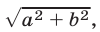запишем его в виде

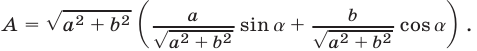
Рассмотрим точку 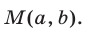Эта точка лежит на окружности радиуса 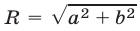с центром в начале координат. Поэтому существует угол 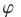такой, что

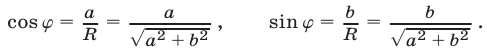
Тогда

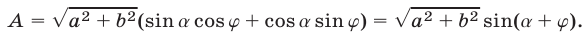
Отсюда следует, что наибольшее значение выражения 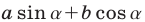равно 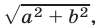а наименьшее значение равно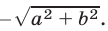

Замечание. При решении этой задачи получено равенство

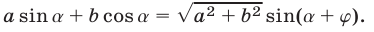
Метод, примененный при преобразовании выражения 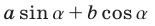а к виду 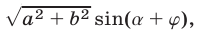называют методом вспомогательного угла.

Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:

Решение задач по математике

Возможно вам будут полезны эти страницы:

Формулы понижения степени с примерами решения

Формулы приведения с примерами решения

Арксинус с примером решения

Арккосинус с примерами решения