В большинстве случаев при измерениях, вычислениях, выполнении операций над действительными числами получаются не точные, а приближенные значения величин.
Приближенным будем называть такое число, которое отличается от точного на погрешность (ошибку), допущенную в соответствии с условиями данной задачи, и заменяет точное число в расчетной формуле.
Основными источниками погрешностей при решении практических задач могут быть:
- Погрешности исходных данных (например, результаты измерений всегда выражаются приближенными числами, точность которых во многом зависит от точности измерительных приборов).
- Погрешности модели (при построении модели невозможно учесть все влияющие на нее факторы. Так, в случае физического явления мы иногда пренебрегаем трением, сопротивлением среды, температурой, поэтому и модель получается приближенной, с погрешностями).
- Методические погрешности (во многих методиках расчета часто используются приближенные формулы. На ближайших занятиях мы познакомимся с методиками приближенного решения уравнений, вычисления определенных интегралов, решения дифференциальных уравнений).
- Операционные погрешности (возникают из-за погрешностей округлений в результате счета, например, при замене
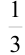десятичной дробью 0,33. Данные и результаты промежуточных операций округляются, вследствие чего накапливаются погрешности).
Введем следующие обозначения:
— точное значение величины;
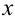— приближенное значение величины (
).
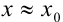Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Переход от тригонометрической и показательной формы. |
| Переход от алгебраической формы к тригонометрической и показательной. |
| Абсолютная погрешность. |
| Относительная погрешность. |
