Оглавление:







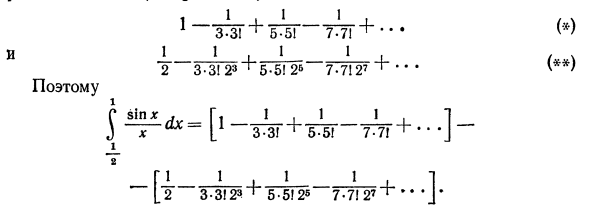

Приложение рядов к приближенным вычислениям
- , Примерный расчет серии приложений Числовые и функциональные ряды широко используются в приближенных расчетах. Укажите наиболее важные из этих приложений. /. Вычисление значений функций с использованием рядов Предположим, что * = и значение функции f (x) необходимо вычислить с определенной точностью. Предположим, что функция может быть расширена в степенных рядах f (x) = a0 + ax (x-a) + …. + a (x-a) n + … Интервал (a- /?, A — \ — R) и точка x = x0 принадлежат этому интервалу. тогда f (* 0) = a, + a, (* o 4 — (* <> — a) 2 -I. • — (x0 — a) n + …
\ Точность этого уравнения увеличивается с увеличением n. Абсолютная погрешность этого приближенного уравнения, т.е. | / (dc0) -S \ f (xJ-Sn (x0) \ = \ rn (x0) \ t где rnW = fl «+ i to a) n + 1 + i„ +2 (x0 — a) «+ * + ..; Если вы хотите вычислить значение функции / — (* c) с точностью e> 0, возьмите сумму из n первых членов,
Если вы получите первый член достаточного количества рядов, вы можете получить приближенное уравнение f (x0) Sn Sn (x0) = a0 + ax (xn-a) + ai (x0-af + … + an (x0-a) Людмила Фирмаль
Метод оценки остальных рядов был введен в § 1, пункт 7. Ниже приведен еще один способ оценки остатка ряда с использованием остатка ряда Тейлора (или Маклаурина). Если функция расширяется степенным рядом, как мы знаем, это ряд Тейлора или Маклаурина (см. § 3, пункт 4). В этом случае абсолютная ошибка, \ f (x0) -S „(xn) \, равна модулю оставшейся части ряда Тейлора (или Маклорина). Вот так I / (,) — S „(,) | = | fln (*,) | = | J- ^ g- (AC.-e) — * ■ 1 с включен между а и х0. В зависимости от каждого конкретного случая, для оценки остальной части ряда используется тот или иной метод. Давайте посмотрим на некоторые примеры. Пример Рассчитать числовое значение e с точностью до 0,001.
Решения. Как известно, разложение (93) может быть любым х Когда х = 1 Получение первого члена i-f-l дает приблизительную эквивалентность «» Я + я + я + я + … + д Оцените погрешность аппроксимации, используя остаточный член ряда Маклаурина. Поскольку f (m + 1) (x) = ex, М = (/ г 4-1)! * I + 1> где c находится между 0 и x. Когда х = 1 Учитывая e ° 0’001 ‘и PRI / r == 6 3 1 <0,001. <04-1)! 1680 Следовательно, n = G достаточно для достижения требуемой точности. Поэтому до 0,001 Ёжик 1 + 1 + 2! + 31 + 41 + 5! + 6! • Запишите каждый термин с одним дополнительным знаком, чтобы ошибки, связанные с округлением терминов, не добавлялись к ошибке. е «1,0000 + 1,0000-L 0,5000 + 0,1667 + 4-0,0417 + 0,0083 + 0,0014 = 2,7181.
| Функциональные ряды | Решение систем линейных уравнений методом Гаусса |
| Степенные ряды | Системы линейных однородных уравнений |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Поэтому с точностью 0,001 е = 2,718. Пример 2. Расчет с точностью 0,0001 до 18 °. Решения. Существует расширение (94) для греха * Все значения х: _, (—L) * -1 ** «-1. Грех ДС-l: 3j-t-5 | • ..- Г- (2 l-1)! + Преобразование 18 ° в радианы дает х =. Таким образом, При чередовании ряда (104) абсолютное значение его членов уменьшается и стремится к нулю. Следовательно, остаток не превышает период, когда он был впервые уничтожен (см. § 1, пункт 7). с того времени 13 л ■ 3> 1Q3> 0,0001 и -5 | 1Q6- <0,0001, затем 0,0001 Все расчеты выполняются с одним дополнительным символом, настройка 71.3.14159. Поскольку n3 = 31,00624, грех 18 ° = 31 ^ из4 = 0,31416 —0,00517 = 0,30899, Таким образом, грех 18 ° «0,3090.
Приблизительный расчет интеграла 1/3 Пример б. Вычислить определенный интеграл J e ~ * r dx с точным интегрированием о До 0,0001. Решения. Антидифференциальный коэффициент e ~ * 2 существует, но не выражается в элементарных функциях, поэтому формула Ньютона-Лейбница не может быть применена для вычисления этого интеграла.
Давайте проиллюстрируем природу метода на примере. Людмила Фирмаль
Следовательно, разложение степенных рядов интегрирует e в x * (см. Уравнение (100)). -x2 1 uii — J in II * 21 31 —- Эта серия сходится по всей оси значений. Так что любой сегмент, особенно обслуживание N1 Иллинойс S-я -x7- 3+. , , = 7 31 | О «—— 3 3-1! 33 5-2I35 7-3! 37» Найденный интеграл равен сумме чередующихся рядов. с того времени Затем в пределах 0,001 на основе правил оценки ошибок для чередующихся рядов (см. § 1, пункт 7), 5-2! 0,3333-0,0123 = 0,3210. Я Я е ~ х * дх Z-Z3
так $ е ~ х * дх ш 0,321 Замечания. Как известно, обратная производная F (x) функции e ~ x * не является элементарной функцией. Интегрируя ряд (100) для каждого члена в диапазоне от 0 до x, его можно легко получить в виде суммы степенных рядов. F (x) = x — 4 -—_ + Г ш л 31! Г 5-2! 7 3! Производная этой функции есть e ~ * r: F ‘(x) -e ~ xZ. Пример 2. Расчет интеграла 1 Грех х Я дх 2 Точность 0,001. Решения. с того времени x3. ху Затем разделите каждую часть этого уравнения на x, чтобы получить разложение Грех x x2, x4 / 1hp \ — = 1-W + 5G ~ — <105> Объединение равенства с обеих сторон (105) дает 1 1. JL _L -L _L 2 2 2 8 2 Результирующий ряд можно рассматривать как разность двух сходящихся чередующихся рядов, которые удовлетворяют условиям теоремы Лейбница (см. § 1, с. 6).
i__L__U J___Li / ч 3-3! «5-5! 7 * 71 ••• l * J J _ 1 . 1 1 , v 2 3-3! 23 ‘5 * 5! 2B 7-7I27 ••• V ** J так j ^ = [, + J _ J + …] _ 2 _G ± ! l 1 [2 3-3! 23 ‘5-5! 2s 7-7! 27 ^’ ‘J * Для IIo, чередующегося ряда, сходящегося на основе Лейбница, ошибка не превышает модуль первого отброшенного члена, 1 <0,001 (для строки х), 7-7! <0,001 (для строки **), тогда j «[l_s ^ + ^ r] — [j-yC * 0.4530. Поэтому с точностью 0,001 ^ = 0,453.
