Применение дифференциала к различным задачам

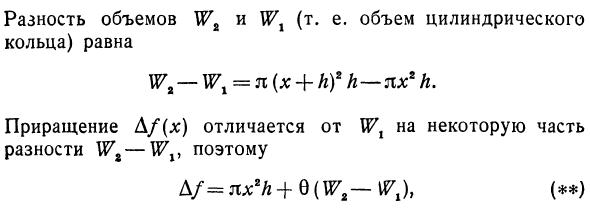
Применение дифференциала к различным задачам

• Дифференциальное применение для различных задач Обсуждение в § 2 не только приводит к концепции дифференцирования, но в некоторых случаях вы можете найти производные. Предположим, что приращение функции выражается как Au = (p (x) A + (o (x, A), (*)Здесь φ (x) не зависит от A, Лм> ч Тогда где ч-н лм> ч- * о н Таким образом, f (q 🙂 является производной данной функции. Пример 1. Найти производную функции f (x), определенной геометрически как граница объема. 1) Поверхность Py, полученная при вращении вокруг оси Ox дуги OA, принадлежащей параболе y = x1 \ 2) По плоскости Pr, перпендикулярной оси Ox и отстоящей от начала координат на x (рис. 74). «1 a <\ n <c. 1 A B o \ XГXОгГ • ftv Рис. 74 Рисунок 75

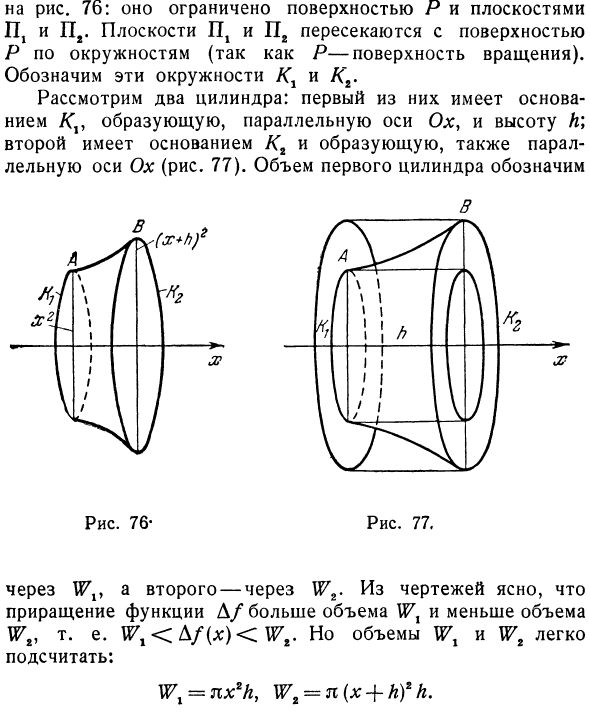
. Возьми любое число jt. Соответствующее значение функции f (x) определяется объемом, окруженным поверхностью P и плоскостью P. Дайте х приращение h. Объем, связанный с этим, то есть функция / (*), получает приращение D /. Этот прирост показан на рисунке. 75 и индивидуальный Рисунок 76: Окружен поверхностью P и плоскостью ITj и P2. Плоскости ITj и P2 пересекают поверхность P с окружностью (поскольку P — поверхность вращения). Эти круги Kx и Kr показаны. Рассмотрим два цилиндра.

Понятно, что объем зависит от величины х, то есть функции от х Людмила Фирмаль

Первый цилиндр имеет основание Kv и высоту A, образованную параллельно оси Ox. Второй имеет базу O2 и генератор, который также параллелен оси Ox (рис. 77). Объем первого цилиндра составляет в Рисунок 76 — Рисунок 77. 2-й до W2 от Wv. Из чертежа ясно, что приращение функции D / больше, чем объем Wx, и меньше, чем объем Wt, то есть Wt <bf (x) <Wt. Однако объем Wl и Wt можно легко рассчитать. Wx = nx2h, Wz = n (x + h) 2h

Разница в объеме между W2 (т.е. объем цилиндрического кольца) составляет Wi-W1 = n (x + h) 2 h-xx2h. Приращение A / (x;) отличается от Wl частью разности Wz-Wv. Таким образом, D / = nx2h + 8 (W2-Wx), (**)Где G — положительное число меньше 1. с того времени I7t-Wx n (x + h) * h— nx * h ободок L ободок Ах ах = lim-yal: a] = 0, Поскольку Q (W2 — справа от уравнения ()) является бесконечно малым высшим порядком по h, уравнение () является частным случаем уравнения (*).

• Таким образом, заключение было сделано в начале раздела. Он также может быть преобразован в равенство (то же самое). То есть производная функции f (x) равна nx2. В этом примере мы должны отметить тот факт, что функция f (x) чисто геометрически определена. Я не знал выражения, определяющего эту функцию, но нашел производную.

Пример 2. . Найдите объем V материала, из которого изготовлена ​​эта труба (Рисунок 78). Этот объем называется объемом цилиндрического слоя. Поскольку объем внешнего цилиндра равен nR2H, а объем внутреннего цилиндра равен tcr2, объем слоя цилиндра равен K = i R2H — nr2H, Рисунок 78.

Рассмотрим цилиндрическую трубу с внешним радиусом / внутренним, внутренним радиусом r и высотой I Людмила Фирмаль

или V = nH (R2-r1) = nR (r + r) (r-r) (♦) Если стенки трубы тонкие, r и R не сильно отличаются друг от друга. Выразите разницу в h (h = R — r). Тогда выражение (*) принимает вид: V = нН (2r + ч) ч, или l / = 2 nHrh + nHh \ (# *) Второе слагаемое в правой части (**) уравнения является квадратичным по отношению к h.

Следовательно, член nHh * является бесконечно малым высоким порядком, таким как h — »- 0. Если вы откажетесь от него, вы получите приблизительное выражение для расчета объема тонкого цилиндра. Богатый слой: () N Интересно отметить еще один способ получить это выражение (рисунок 79). Если трубка разрезана вдоль своей образующей и повернута на плоскости, получается «почти» кубоид с измерениями 2π, A и H. Его объем составляет 2 r rHh, который получается из уравнения ().

Смотрите также:

Предмет высшая математика

Дифференциал	Первообразная и неопределенный интеграл
Применение к приближенным вычислениям	Преобразования неопределенных интегралов