Пример решённой на заказ задачи №89.
Исследовать на экстремум функции: 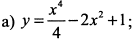
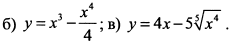
Решение:
а) Находим первую производную 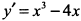 и приравниваем ее к нулю
и приравниваем ее к нулю 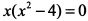 . Корни этого уравнения:
. Корни этого уравнения: 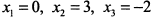 являются критическими точками.
являются критическими точками.
Находим вторую производную 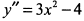 и выясним знак второй производной в критических точках:
и выясним знак второй производной в критических точках: 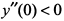 — функция имеет максимум;
— функция имеет максимум; 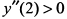 — функция имеет минимум;
— функция имеет минимум; 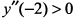 — функция имеет минимум. Определяем экстремальные значения функции:
— функция имеет минимум. Определяем экстремальные значения функции: 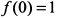 — максимум функции;
— максимум функции; 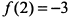 — минимум функции;
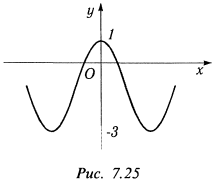
— минимум функции; 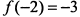 — минимум функции. График функции показан на рис. 7.25.
— минимум функции. График функции показан на рис. 7.25.
б) Находим первую производную 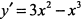 и приравниваем ее к нулю
и приравниваем ее к нулю 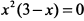 . Корни этого уравнения:
. Корни этого уравнения: 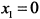 ,
, 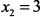 являются критическими точками.
являются критическими точками.
Находим вторую производную 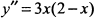 и выясним знак в критических точках.
и выясним знак в критических точках.
При 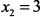 вторая производная
вторая производная 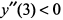 — функция имеет максимум. При
— функция имеет максимум. При 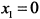 вторая производная
вторая производная 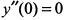 , следовательно, судить об экстремуме нельзя. Проверим наличие экстремума по первой производной. Поскольку при переходе через точку
, следовательно, судить об экстремуме нельзя. Проверим наличие экстремума по первой производной. Поскольку при переходе через точку 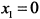 первая производная знака не меняет, то в точке
первая производная знака не меняет, то в точке 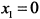 экстремума нет.
экстремума нет.
Определяем в точке 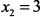 максимальное значение функции
максимальное значение функции 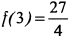 .
.
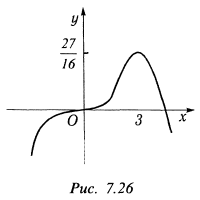
График функции показан на рис. 7.26.
в) Функция определена на всей числовой оси. Находим производную 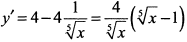 . Приравниваем производную к нулю
. Приравниваем производную к нулю 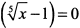 и находим критическую точку
и находим критическую точку 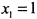 . При переходе через точку
. При переходе через точку 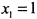 производная
производная 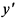 меняет знак с минуса на плюс, следовательно, в точке
меняет знак с минуса на плюс, следовательно, в точке 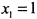 функция имеет минимум
функция имеет минимум 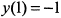 .
.
Приравнивая к нулю знаменатель производной, получаем 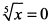 . Отсюда находим критическую точку функции
. Отсюда находим критическую точку функции 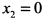 , в которой производная не существует. Очевидно, что в точке
, в которой производная не существует. Очевидно, что в точке 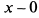 производная
производная 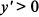 , а в точке
, а в точке 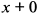 производная
производная 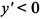 . Следовательно,
. Следовательно, 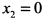 есть точка максимума функции
есть точка максимума функции 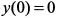 (рис. 7.27).
(рис. 7.27).
На этой странице найдёте ещё больше примеров с решением по всем темам высшей математики и сможете заказать решение:
Заказать решение заданий по высшей математике
Для вас подобрала похожие примеры с решением возможно они вам пригодится:
| Пример решённой на заказ задачи №85. |
| Пример решённой на заказ задачи №87. |
| Пример решённой на заказ задачи №91. |
| Пример решённой на заказ задачи №93. |
