Оглавление:
Системы, содержащие логарифмы с постоянными основаниями
Рассмотрим системы логарифмических уравнений, в которых содержатся логарифмы с постоянными основаниями. При решении таких систем часто используется формула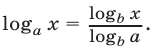 
Примеры с решениями
Пример №212.
Решить систему уравнений
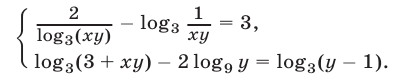
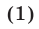
Решение:
Система (1) имеет смысл лишь в том случае, когда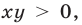 
т. е. при выполнении условий
Полагая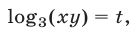 
запишем первое уравнение системы (1) в виде 
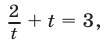откуда 
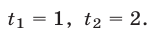Если 
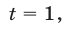, то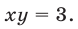 
В этом случае система (1) примет вид
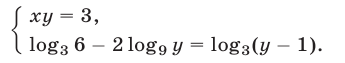
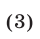
Если 
то 
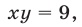и система (1) примет вид
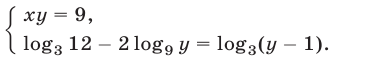
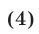
Рассмотрим систему (3). Так как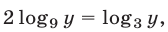 
то второе уравнение этой системы равносильно уравнению
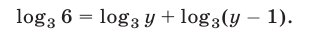
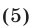
Потенцируя, получаем уравнение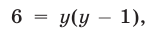 
являющееся следствием уравнения (5) и имеющее корни 
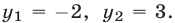. Значение 
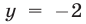не удовлетворяет условию (2), а при 
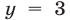из первого уравнения системы (3) находим 
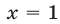. Пара чисел 
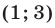— решение системы (1).
Аналогично, решив систему (4), найдем еще одно решение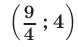 
; системы (1).
Ответ.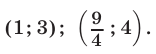 
Пример №214.
Решить систему уравнений
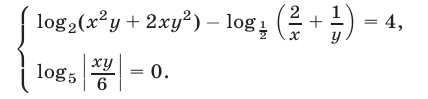
Решение:
Первое уравнение системы можно записать в виде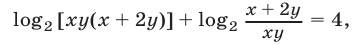 
а множество допустимых значений 
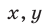определяется условием
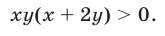
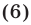
При выполнении условия (6) исходная система равносильна системе
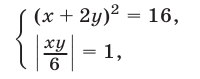
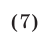
а система (6)-(7) равносильна совокупности двух систем
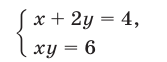
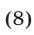
и
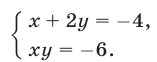
Исключая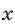 
из системы (8), получаем уравнение 
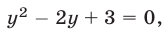не имеющее действительных корней. Поэтому система (8) не имеет действительных решений.
Из системы (9) получаем уравнение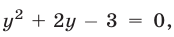 
имеющее корни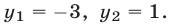 
Поэтому исходная система имеет два решения: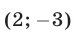 
и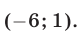 
Ответ.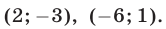 
Пример №215.
Решить систему уравнений
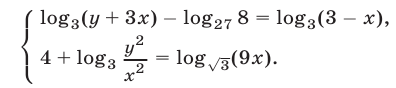
Решение:
Считая, что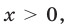 
и переходя к логарифмам по основанию 3, заменим исходную систему равносильной ей:
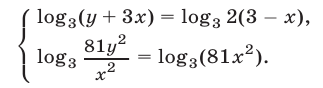
Потенцируя, получаем систему
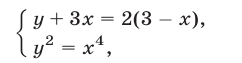
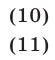
являющуюся следствием исходной системы. Из (11) следует, что 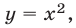либо 
либо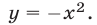 
1) Если 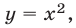, то из (10) получаем уравнение 
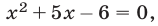откуда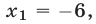 
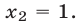При 
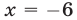исходная система теряет смысл. При 
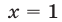имеем 
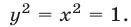Пара чисел 
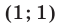— решение исходной системы.
2) Если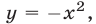 
то из (10) получаем уравнение 
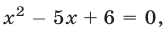имеющее корни 2 и 3. При 
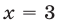исходная система теряет смысл. При 
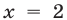находим 
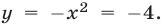Пара чисел 
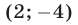образует решение исходной системы.
Ответ.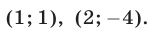 
Пример №216.
Решить систему уравнений
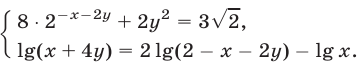
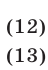
Решение:
Потенцируя, заменим (13) на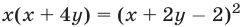 
или
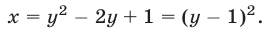
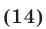
Система (12), (14) является следствием системы (12), (13). Исключив 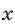из системы (12), (14), приходим к уравнению
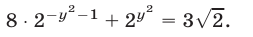
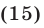
Полагая в (15)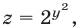 
получаем уравнение 
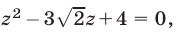откуда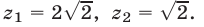 
1) Если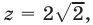 
то 
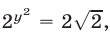откуда 
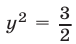и из (14) следует, что 
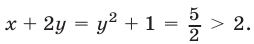В этом случае правая часть уравнения (13) теряет смысл.
2) Если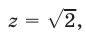 
то 
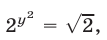откуда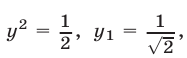 
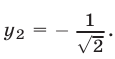Из уравнения (14) находим 
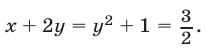При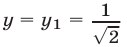
.
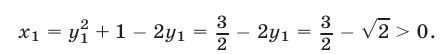
В этом случае выражения, содержащиеся под знаками логарифмов в уравнении (13), положительны и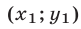 
— решение системы (12), (13). При 
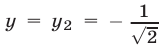имеем 
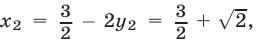
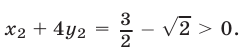Пара чисел 
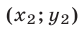также образует решение системы (12), (13).
Ответ.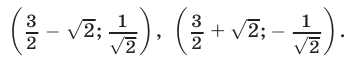 
Пример №217.
Решить систему уравнений
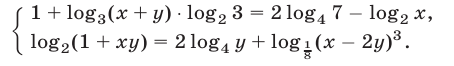
Решение:
Используя равенство
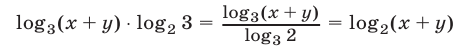
и переходя к логарифмам по основанию 2, получим систему
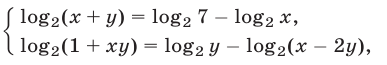
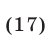
равносильную системе (16). Потенцируя, приходим к системе
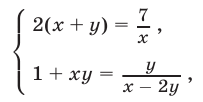
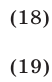
являющейся следствием системы (17). Из уравнения (18) следует, что
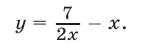
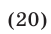
Подставляя это в уравнение (19), получаем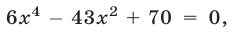 
откуда 
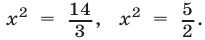Так как при 
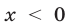первое уравнение системы (16) теряет смысл, то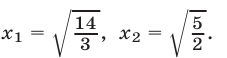 
Если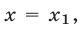 
то из (20) имеем 
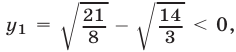тогда как второе уравнение системы (16) имеет смысл лишь при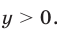 
Если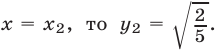 
Проверка показывает, что пара чисел 
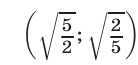является решением системы (16).
Ответ.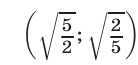
Пример №218.
Решить систему уравнений
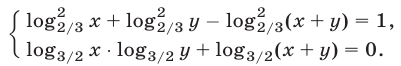
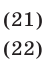
Решение:
Переходя в уравнении (22) к логарифмам по основанию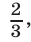 
получаем
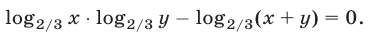
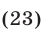
Складывая уравнение (21) с удвоенным уравнением (23), имеем
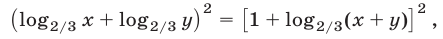
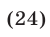
откуда
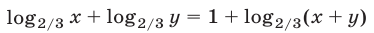
или
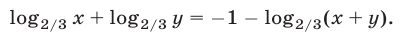
Система (21), (22) равносильна совокупности систем (23), (25) и (23), (26).
1) Рассмотрим систему (23), (25). Из (25) следует, что
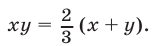
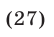
Исключая из уравнений (23) и (25)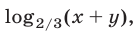 
получаем
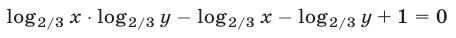
или
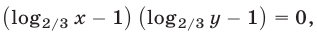
откуда следует, что 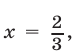либо 
либо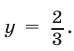 
Но если 
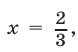то равенство (27) не может быть верным ни при каких значениях 
.
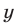Аналогичное утверждение справедливо и при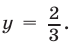 
Таким образом, система (23), (25) не имеет решений.
2) Рассмотрим систему (23), (26). Из уравнения (26) следует, что
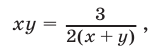
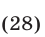
а из (23) и (26) находим
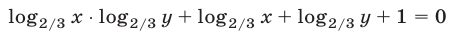
или
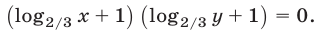
Если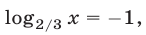 
то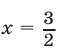 
и тогда из уравнения (28) получаем 
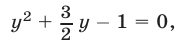откуда 
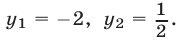Значение 
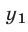следует отбросить, так как при 
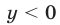исходная система теряет смысл.
Если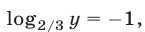 
то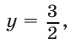 
и из (24) найдем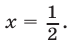 
Ответ.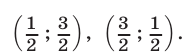 
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
