Приведение силы к точке
Ранее мы установили, что вектор силы можно переносить по линии действия в любую точку тела.
Попробуем силу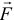 
(рис. 5.1) перенести в какую-нибудь точку 
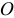, не расположенную на линии действия.
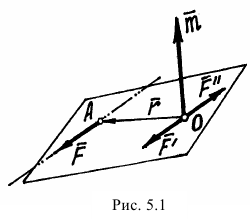
Приложим к этой точке две уравновешивающиеся силы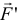 
и 
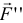, параллельные силе 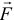и равные ей по величине, 
.
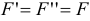В результате получим силу 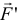равную силе 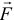и приложенную к точке 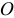. То есть мы как бы перенесли заданную силу 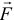из точки 
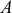в точку 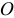, но при этом появилась пара, образованная силами 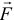и 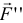. Момент этой пары
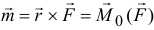
равен моменту заданной силы 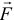относительно точки .
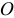Процесс замены силы 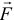равной ей силой 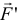приложенной к точке 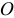, и парой называется приведением этой силы к точке .
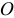Точка 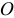называется точкой приведения; сила 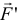приложенная к точке приведения, — приведенной силой. Появившаяся пара — присоединенной парой.
- Сложение сил, произвольно расположенных в пространстве
Пусть дана система, состоящая из нескольких произвольно расположенных сил (на рис. 5.2 показаны три силы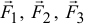 
). Требуется сложить эти силы и посмотреть, что в результате получится.
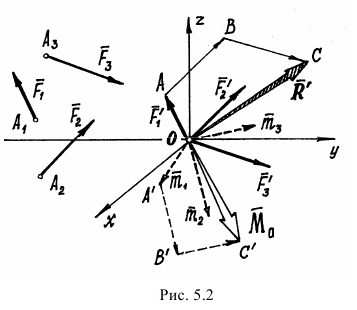
Приведем все силы к произвольно выбранной точке 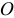, центру приведения. Получим систему приведенных сил, приложенных к точке 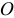, равных заданным силам: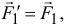 
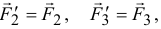, и систему присоединенных пар, моменты которых равны векторам моментов заданных сил относительно центра приведения :
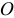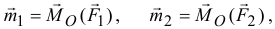
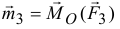
Сложив первую систему, систему сходящихся приведенных сил, например, построением многоугольника сил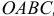 
, получим их равнодействующую 
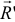которая равна векторной сумме этих приведенных сил, а значит, и заданных сил, потому что они векторно равны
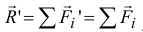
А сложив систему пар, например, построением многоугольника их векторов моментов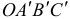 
, получим пару, момент которой 
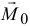равен векторной сумме моментов присоединенных пар или сумме моментов заданных сил относительно центра приведения
Сила 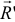равная векторной сумме заданных сил, называется главным вектором этих сил. Приложена эта сила к центру приведения.
Момент 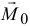равный векторной сумме моментов заданных сил относительно центра приведения, называется главным моментом этих сил относительно центра приведения.
Главный вектор 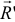можно найти так же, как находили ранее равнодействующую сходящихся сил (см. И, §2, формула (2.2)).
Проекции его на оси (см. рис. 5.2)
Поэтому модуль главного вектора
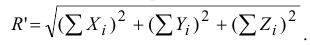
Направление вектора 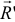определяется с помощью направляющих косинусов:
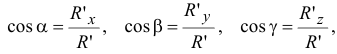
где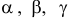 
— углы между вектором 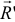и направлением осей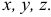 
Так как векторы моментов присоединенных пар также образуют систему сходящихся векторов, то и главный момент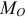 
находим аналогичным способом
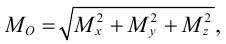
где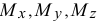 
— проекции вектора 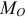на оси. Проектируя его на оси, получим, принимая во внимание, что проекция вектора момента силы относительно точки на ось, проходящую через эту точку, есть момент относительно оси (3.4):
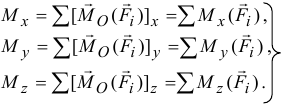
Эти проекции 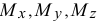— вектора главного момента 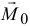на оси, равные алгебраическим суммам моментов заданных сил относительно осей, проходящих через центр приведения, называются главными моментами сил относительно соответствующих осей.
Модуль главного момента 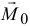находится по (5.4) или с учетом (5.5)
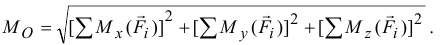
Направление этого вектора можно найти с помощью направляющих косинусов
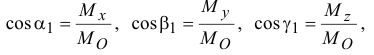
где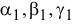 
— углы между 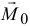и направлением осей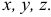
Итак, при сложении сил, произвольно расположенных в пространстве, в общем случае получается сила 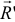, приложенная к центру приведения, и пара с моментом .
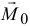Два важных замечания. Первое — главный вектор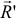 
не является равнодействующей 
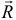заданных сил, так как он не может один заменить действие всех сил, а только вместе с парой.
Второе — главный вектор 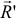как векторная сумма заданных сил не зависит от положения центра приведения. А главный момент 
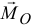зависит, так как моменты заданных сил относительно центра приведения изменятся, если этот центр будет в другом месте.
Конечно, возможны различные результаты сложения сил.
- Может оказаться, что главный момент относительно выбранного центра приведения
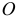окажется равным нулю 
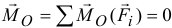, а главный вектор 
.
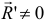Это значит, что в результате сложения получится только сила, равная главному вектору. И она, эта сила, в данном частном случае является равнодействующей 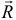всей системы сил. Линия действия равнодействующей будет проходить через этот центр приведения.
В этом частном случае имеет место очень важная и полезная теорема — теорема Вариньона.
Пусть на тело действует несколько сил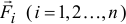 
и у них существует равнодействующая 
, приложенная к центру приведения 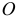(рис. 5.3).
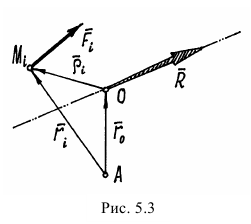
Покажем радиусы-векторы, проведенные из некоторой точки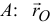 
— радиус-вектор точки приложения равнодействующей; 
— точек 
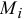, точек приложения сил 
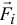, где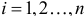 
. И добавим векторы 
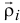, соединяющие точку 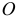сточками .
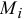Момент сил 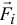относительно точки 
:
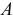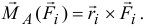
А так как
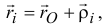
то
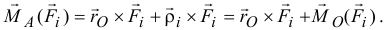
Сумма моментов всех действующих сил 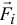относительно точки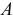
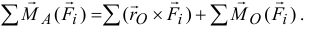
но
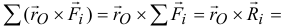
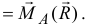
А сумма
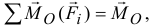
равна главному моменту сил относительно точки 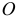, который в этом частном случае равен нулю. Поэтому
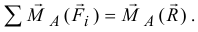
Если у системы сил имеется равнодействующая, то момент равнодействующей относительно любой точки 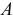равен векторной сумме моментов всех сил относительно этой точки
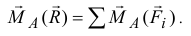
Следствие. Если спроектировать это векторное равенство на какую-нибудь ось, например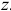 
, проходящую через точку 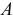, то, имея в виду доказанный ранее результат (3.4), получим теорему Вариньона в другой форме.
Если у системы сил имеется равнодействующая, то момент ее относительно любой оси равен алгебраической сумме моментов всех сил относительно этой оси
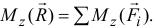
- Возможен и другой случай, при котором, наоборот, главный вектор равен нулю
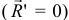, а главный момент относительно данного центра 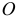не равен нулю 
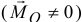. Это означает, что в результате сложения сил получится только пара с моментом 
.
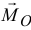А так как момент пары сил относительно любой точки равен моменту этой пары (IV, §2), то в этом случае, когда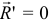 
, главный момент не зависит от выбора центра приведения. Относительно любой точки 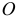он будет одинаков и равен
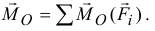
И, наконец, может оказаться, что и главный вектор 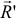и главный момент 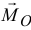равны нулю. В этом случае силы уравновешиваются, а тело под действием этих сил находится в равновесии.
А так как
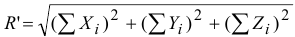
и главный момент
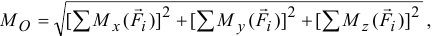
то для равновесия тела необходимо выполнение шести условий
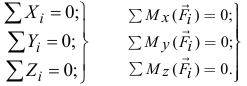
Эти условия называются уравнениями равновесия сил, произвольно расположенных в пространстве.
В частности, если силы расположены в одной плоскости, то, направив оси так, чтобы ось 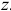стала перпендикулярна этой плоскости, третье уравнение 
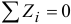, четвертое 
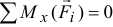и пятое 
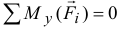обратятся в тождества, а в шестом — моменты сил относительно оси 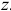будут равны моментам относительно точки 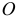, точки пересечения оси и плоскости.
Останутся только три уравнения из шести:
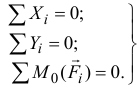
Так как в системе уравнений (5.10) уравнения моментов удовлетворяются относительно любой оси, то таких уравнений моментов можно составить больше трех, хоть все шесть.
Точно так же в системе уравнений (5.11) для плоской системы сил можно составить и два, и три уравнения моментов. Поэтому возможны три варианта
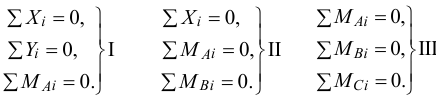
Правда, имеются ограничения на выбор точек и осей. Например, при использовании II варианта точк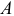и 
и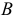 
не должны лежать на прямой, перпендикулярной оси; а в III варианте — точк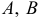и 
и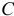 
не должны располагаться на одной прямой.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Зависимость между моментами силы относительно точки и относительно оси |
| Пара сил. Момент, свойства, сложение пары сил |
| Сложение параллельных сил. Центр параллельных сил |
| Центр тяжести тел |
