Оглавление:


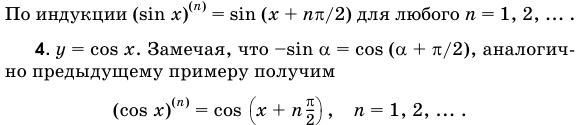

Производные высших порядков
Производные высших порядков. Определение 1.Пусть функция f (x), определенная в интервале (a, b), имеет производную A ’(x) в каждой точке x∈(a, b) и равна x∈(a, b). если x = x, то производная функции A (x) называется 2-й производной (или 2-й производной) функции A, обозначаемой A’ (x) или A (2) (x). Итак, a » (x)= [A ’(x)’] ’| x = xo, или опустите обозначение аргумента, y «=(y’)’.Любой порядок n = 1, 2,…Производная y (n) аналогично определяется, если существует производная y (n 1) Порядка n-1 (в этом случае производная нулевого порядка сама по себе Под функцией y () = y, а 1-я производная-y’), по определению, получаем y (n = [y (n 1)]’. А(n) (х) = Хм Дуплексный<sup class=»reg»>®</sup> А(N 1}(х-я-ДХ) А(Н 1}(х)DX n = 1, 2,….
Все, что мы здесь говорим, естественно переносится на так называемые односторонние производные высшего порядка, которые читатель легко может определить для себя сам. Людмила Фирмаль
- Напомним определение производных (см.§ 9.1), определение N-й производной в x может быть записано как ограничение. Учитывая предположение, что функция A имеет производную Порядка n в точке x, по последнему определению, в некоторой окрестности точки x функция A имеет производную Порядка n-1, и поэтому в n 1 все производные определяются в окрестности x, в частности, сама функция определяется в окрестности точки X. x. In кроме того, все производные, порядок которых меньше n-1, являются смежными в указанной окрестности. 3 4 Поскольку во всех отношениях они имеют производные (см. теоремы 9.2, 1 и 2).
- Определение 2.At все точки этого интервала, непрерывные производные до степени n(n=, 1, 2,…Если есть a), то функция называется непрерывной дифференцируемой n раз в определенном интервале. Кроме того, как обычно, под производной понимается соответствующая односторонняя производная на любом конце рассматриваемого интервала, когда этот конец принадлежит промежутку. Для того чтобы функция была N раз непрерывной дифференцируемой на определенных интервалах, достаточно иметь непрерывную производную Порядка n на it.
Дело в том, что согласно определению, если в рассматриваемом интервале имеется производная Порядка n, то на ней имеется производная порядка n-1. Людмила Фирмаль
- In существование производной функции в определенной точке подразумевает непрерывность функции в этой точке, как уже было сказано выше, а производная Порядка n-1 непрерывна на заданном интервале. Аналогично для случая n 1 доказана непрерывность в рассматриваемом интервале производной Порядка n-2. Образцы. 1. y = хр, у ’= 3×2,у = 6х, у(П)= 6,у(4)= г(ч)= 。 =. В индукции (81n x) (n)= 81n (x + pr / 2), n = 1, 2,…. 4. y =soy x. 8 m a = soy(a + mc / 2), как и в предыдущем примере、 (co8 х) (н)= С8(х + Н2), где N = 1, 2,…
Смотрите также:
