Задача №16.
Прямолинейный стержень 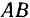 скользит своими концами по двум взаимно перпендикулярным направляющим
скользит своими концами по двум взаимно перпендикулярным направляющим 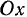 и
и 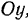 вращающимся вокруг точки
вращающимся вокруг точки 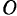 с постоянной угловой скоростью
с постоянной угловой скоростью 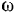 . Угол наклона стержня
. Угол наклона стержня 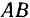 к оси
к оси 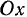 изменяется по закону
изменяется по закону
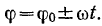
Определить абсолютную траекторию произвольной точки 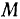 стержня.
стержня.
Решение:
Предположим, что угол 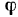 изменяется по закону
изменяется по закону 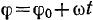 , и пусть стержень .имеет длину
, и пусть стержень .имеет длину 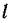 . Стержень в этом случае участвует в двух движениях: вместе с подвижной системой (направляющими) он вращается с угловой скоростью
. Стержень в этом случае участвует в двух движениях: вместе с подвижной системой (направляющими) он вращается с угловой скоростью 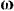 против часовой стрелки и относительно подвижной системы отсчета вращается с такой же угловой скоростью
против часовой стрелки и относительно подвижной системы отсчета вращается с такой же угловой скоростью 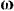 .по часовой стрелке. Мгновенный центр вращения в подвижной системе находится в точке
.по часовой стрелке. Мгновенный центр вращения в подвижной системе находится в точке 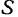 , расположенной, на пересечении перпендикуляров к осям
, расположенной, на пересечении перпендикуляров к осям 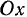 и
и 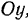 восстановленных из концов стержня
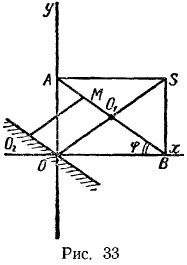
восстановленных из концов стержня 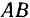 (рис. 33). Результирующее движение в этом случае представляется парой вращений, эквивалентной мгновенно-поступательному движению твердого тела, скорость которого равна моменту пары
(рис. 33). Результирующее движение в этом случае представляется парой вращений, эквивалентной мгновенно-поступательному движению твердого тела, скорость которого равна моменту пары 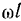 . Скорость центра стержня во все время движения остается постоянной по величине и направлена ортогонально к прямой
. Скорость центра стержня во все время движения остается постоянной по величине и направлена ортогонально к прямой 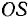 , а следовательно, центр стержня движется по окружности с постоянной скоростью. Чтобы определить траекторию точки
, а следовательно, центр стержня движется по окружности с постоянной скоростью. Чтобы определить траекторию точки 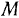 , воспользуемся тем обстоятельством, что стержень совершает поступательное движение. Построим на прямых
, воспользуемся тем обстоятельством, что стержень совершает поступательное движение. Построим на прямых 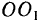 и
и 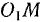 параллелограмм. Сторона
параллелограмм. Сторона 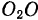 этого параллелограмма остается неподвижной во все время движения, а точка
этого параллелограмма остается неподвижной во все время движения, а точка 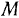 будет двигаться по окружности с центром, в точке
будет двигаться по окружности с центром, в точке 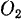 .
.
Рассмотрим второй случай, когда
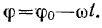
Угол 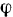 убывает, и стержень совершает два происходящие против часовой стрелки вращения. Результирующее движение является мгновенным вращением с мгновенной угловой скоростью
убывает, и стержень совершает два происходящие против часовой стрелки вращения. Результирующее движение является мгновенным вращением с мгновенной угловой скоростью 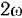 , причем линия действия вектора мгновенной угловой скорости -проходит через центр стержня
, причем линия действия вектора мгновенной угловой скорости -проходит через центр стержня 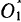 . Поэтому скорость точки
. Поэтому скорость точки 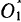 будет постоянно оставаться равной нулю, а все остальные точки стержня будут описывать концентрические окружности вокруг точки
будет постоянно оставаться равной нулю, а все остальные точки стержня будут описывать концентрические окружности вокруг точки  .
.
В общем случае мгновенное движение твердого тела может быть задано как сложное движение, состоящее из нескольких мгновенно-поступательных и мгновенно-вращательных движений. Такое общее движение всегда можно свести к более простому мгновенному движению — мгновенно-винтовому движению твердого тела. При этом задача сводится к приведению системы скользящих векторов, каковыми являются вектора мгновенной угловой скорости вращения твердого тела, к простейшему виду.
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
