Оглавление:
Решение многих задач с параметрами, предлагаемых на вступительных экзаменах, требует умения правильно формулировать необходимые и достаточные условия, соответствующие различным случаям расположения корней квадратного трехчлена на числовой оси.
Пусть квадратный трехчлен 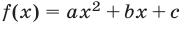 имеет корни
имеет корни 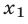 и
и 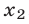 ,
, 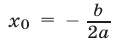 абсцисса вершины параболы
абсцисса вершины параболы 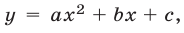
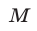 и
и 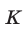 — заданные числа.
— заданные числа.
Справедливы следующие утверждения, связанные с расположением точек 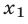 и
и 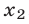 на числовой оси.
на числовой оси.
1°. Для того чтобы оба корня квадратного трехчлена были меньше 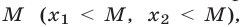 необходимо и достаточно выполнение условий
необходимо и достаточно выполнение условий
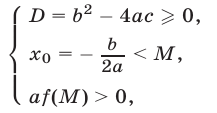
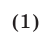
где 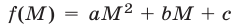 — значение квадратного трехчлена при
— значение квадратного трехчлена при 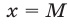 (рис. 21.6 и 21.7).
(рис. 21.6 и 21.7).
В частности, 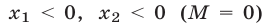 тогда и только тогда, когда выполняются условия
тогда и только тогда, когда выполняются условия
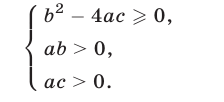
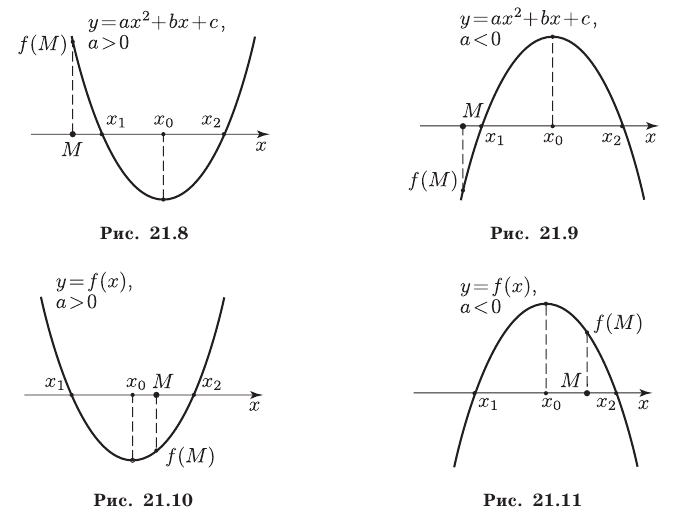
2°. Для того чтобы оба корня квадратного трехчлена были больше 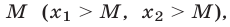 необходимо и достаточно выполнение условий
необходимо и достаточно выполнение условий
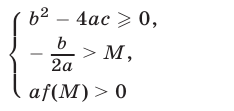
(рис.21.8 и 21.9).
В частности, 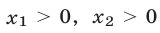 тогда и только тогда, когда выполняются условия
тогда и только тогда, когда выполняются условия
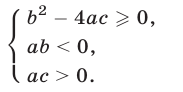
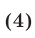
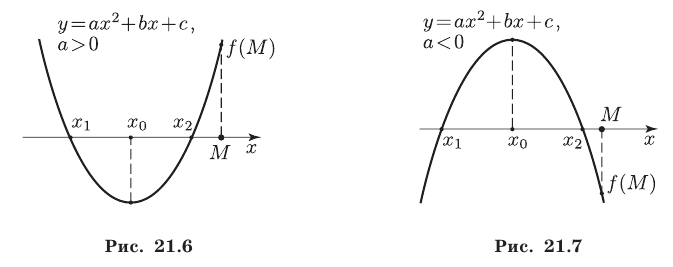
3°. Для того чтобы число 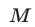 было расположено между корнями квадратного трехчлена
было расположено между корнями квадратного трехчлена 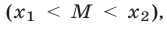 необходимо и достаточно выполнение условия
необходимо и достаточно выполнение условия
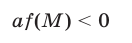
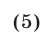
(рис. 21.10 и 21.11).
4°. Для того чтобы оба корня квадратного трехчлена лежали в интервале 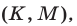 т.е.
т.е. 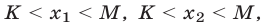 необходимо и достаточно выполнение условий
необходимо и достаточно выполнение условий
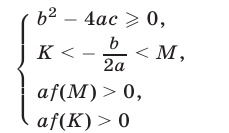
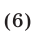
(рис. 21.12 и 21.13).
Заметим, что в условиях (6) последние два неравенства можно заменить одним неравенством
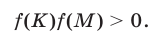
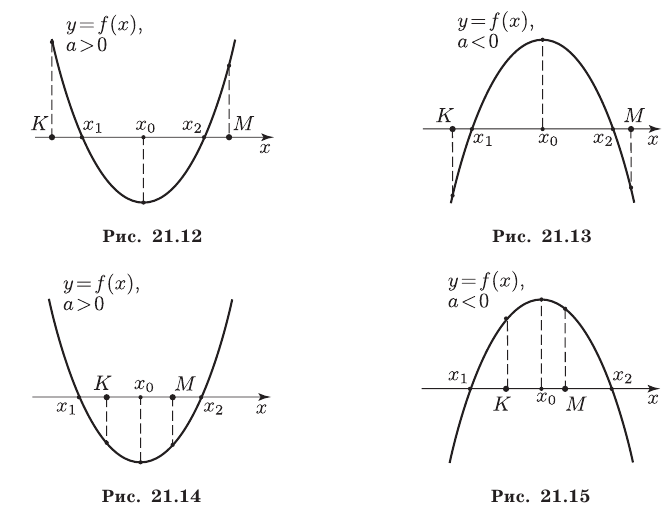
5°. Для того чтобы отрезок 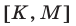 лежал в интервале
лежал в интервале 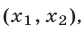 необходимо и достаточно выполнение условий
необходимо и достаточно выполнение условий
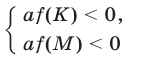
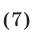
(рис. 21.14 и 21.15).
Ограничимся доказательством утверждения 1°. Квадратный трехчлен 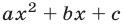 имеет действительные корни
имеет действительные корни 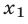 и
и 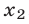 тогда и только тогда, когда
тогда и только тогда, когда
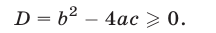
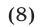
Эти корни удовлетворяют условиям 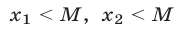 тогда и только тогда, когда
тогда и только тогда, когда

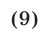
Неравенства (9) выполняются в том и только в том случае, когда, наряду с условием (8), справедливы неравенства
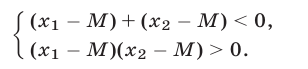
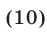
Используя формулы Виета
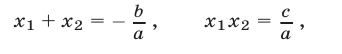
получим систему неравенств
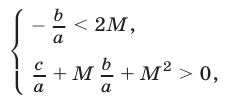
в которой второе неравенство равносильно неравенству 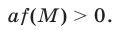
Итак, корни 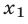 и
и 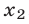 квадратного трехчлена
квадратного трехчлена 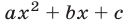 удовлетворяют условиям
удовлетворяют условиям 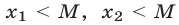 тогда и только тогда, когда коэффициенты
тогда и только тогда, когда коэффициенты 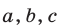 удовлетворяют системе неравенств (1).
удовлетворяют системе неравенств (1).
Аналогично доказываются утверждения 2°-5°, связанные с расположением корней квадратного трехчлена.
Примеры с решениями
Пример №262.
Найти все значения 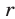 , при которых корни уравнения
, при которых корни уравнения
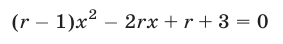
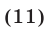
положительны.
Решение:
Корни квадратного уравнения 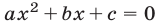 положительны тогда и только тогда, когда выполняются условия (4). Для уравнения (11) при
положительны тогда и только тогда, когда выполняются условия (4). Для уравнения (11) при 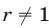 эти условия записываются в виде:
эти условия записываются в виде:
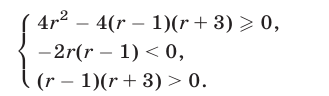
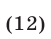
Первые два неравенства системы (12) равносильны соответственно неравенствам

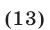
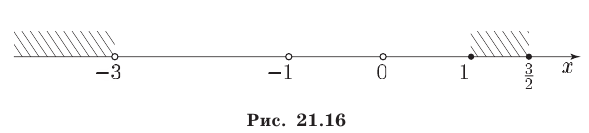
Первое из неравенств (13) справедливо при 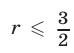 (рис. 21.16),
(рис. 21.16),
второе — при 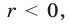 а также при
а также при 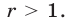 Решениями третьего неравенства системы (12) являются значения
Решениями третьего неравенства системы (12) являются значения 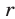 такие, что
такие, что 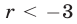 или
или 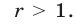 Таким образом, множество решений системы (12) — объединение промежутков
Таким образом, множество решений системы (12) — объединение промежутков 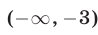 и
и 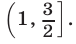
Если 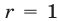 , то уравнение (11) примет вид
, то уравнение (11) примет вид 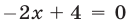 , откуда
, откуда 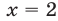 , т.е. корень уравнения (11) при
, т.е. корень уравнения (11) при 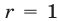 положителен.
положителен.
Ответ. 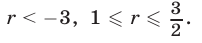
Пример №263.
Найти все значения 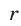 , при которых квадратный трехчлен
, при которых квадратный трехчлен 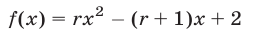 имеет действительные корни
имеет действительные корни 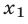 и
и 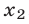 такие, что
такие, что 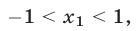
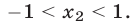
Решение:
В силу утверждения 4°, искомые значения 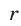 являются решениями системы неравенств (6), которая в данном случае имеет вид
являются решениями системы неравенств (6), которая в данном случае имеет вид
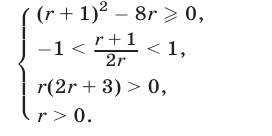
Эта система равносильна каждой из следующих систем:
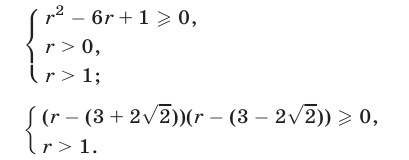
Так как 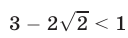 , то в результате получаем
, то в результате получаем 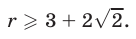
Ответ.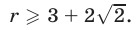
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:
| Квадратный трехчлен и квадратные неравенства с примерами решения |
| Примеры решения рациональных неравенств |
| Иррациональные неравенства с примерами решения |
| Показательные неравенства с примерами решения |
