Оглавление:









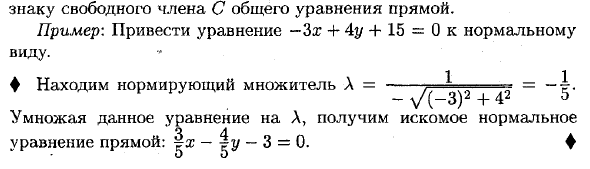
Различные виды уравнений прямой на плоскости
- Различные типы уравнений, действующих непосредственно на плоскости Самая простая линия — это прямая линия. Различные способы определения прямых соответствуют различным типам уравнений в декартовых системах координат. 1. Линейное уравнение с угловым коэффициентом Дает произвольную прямую линию на плоскости Ohu, которая не параллельна оси Oy. Его положение полностью определяется ординатой b пересечения N (Q; b) с осью Oy и углом a между осью Oh и линией. Под углом o; (0 ^ a <n) Наклон прямой — это наименьший угол, на который ось Ox вращается вокруг пересечения прямой и оси Ox, пока не совпадет с прямой.
Возьмем любую точку M (x; y) на прямой. Нарисуйте ось Nx \, которая проходит через точку N, параллельную оси Ox, и направьте ее в том же направлении. В системе Nx’y координаты точки M равны x и y-b. Из определения тангенса угла tan a = V + -, то есть y = tan a • x + b. Я представлю х Значение tga = A: получить уравнение а) Y = kx + 6
Угол между осью Nx ‘и линией равен a. Людмила Фирмаль
Знак свободного члена C общего уравнения для прямой. Пример: приведите уравнение -3x-b 4y + 15 = 0 к стандартной форме. ♦ Коэффициент нормализации Л = — ^ Д3 ^ 2 + 42 = Умножьте это уравнение на A, чтобы получить желаемое нормальное уравнение для линии. — 3 = 0.Это удовлетворяется координатами любой точки M (x; y) на прямой.
Вы можете видеть, что любая точка P (x; y) <координаты вне данной линии не удовлетворяет уравнению (1). Число k = tga называется угловым коэффициентом линии, а уравнение (1) называется уравнением линии с угловым коэффициентом. Если линия проходит через начало координат, 6 = 0, то форма этого уравнения линии будет y = kx. Если линия параллельна оси Ox, то a = 0, поэтому k = tga = 0, и уравнение (1) принимает вид y = b. Если линия параллельна оси Oy, уравнение (1) теряет смысл. Для этого угловой коэффициент k = tga = tg? (= Os)
| Преобразование системы координат | Прямая линия на плоскости. Основные задачи |
| Уравнение линии на плоскости, примеры | Окружность |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Не существует В этом случае линейное уравнение имеет вид х = а, (2) Где а — абсцисса пересечения линии и оси Ox. Обратите внимание, что уравнения (1) и (2) являются линейными уравнениями. 2. Общее уравнение прямой Рассмотрим уравнение первого порядка относительно общего вида x и y. Ax + By + C = 0, (3) Где A, B и C — произвольные числа, а A и B — одновременно ненулевые. Уравнение (3) указывает, что это линейное уравнение. Есть два случая. Если B = 0, форма уравнения (3) имеет вид Ax + C = 0, AΦ0, т.е. x = -Это линейное уравнение, параллельное оси Oy и проходящее через точку В случае ΦΦ0 y =-получается из уравнения (3).
Это линейное уравнение с угловым коэффициентом k = tgc * = -. Некоторые частные случаи общего уравнения прямой: 1) Если A = 0, уравнение сводится к виду y =. Это линейное уравнение, параллельное оси Ox 2) Когда B = 0, линия параллельна оси Oy. 3) Если C = 0, получить Ax + By = 0. Координаты точки 0 (0; 0) удовлетворяют уравнению, и линия проходит через начало координат.
Следовательно, уравнение (3) является линейным уравнением и называется общим линейным уравнением. Людмила Фирмаль
Линейное уравнение через заданную точку В этом направлении Сделайте так, чтобы линия проходила через точку M (x0; y0), и ее направление характеризуется угловым коэффициентом k. Уравнение для этой линии можно записать в виде y = kx 4-6. Поскольку прямая проходит через точку M (x0, y0), координаты точки удовлетворяют уравнению линии y0 = kx o + b.
Следовательно, 6 = уо-кхо. Подставляя значение b в выражение y = kx + b, получаем искомое выражение для строки y = kx + yo-kx0. у-йо = к (х-хо). (4) Уравнение (4) с различными значениями k также называется уравнением пучка вокруг точки M (x0 ‘, Y0). • Из этого карандаша невозможно определить только прямые линии, параллельные оси Oy. 4. Уравнение прямой, проходящей через две точки Пусть прямая проходит через точки M \ (x \ y ) и M2 (x2 ‘, Y2). Форма уравнения для прямой, проходящей через точку Mb: Y ~ 2 / i = k (x-zi), (5) Где k — неизвестный коэффициент Поскольку прямая проходит через точку M2 (^ 22/2)>, координаты этой точки должны удовлетворять уравнению (5): Y2-Y1- = k (x2-x1).
Найти k = ^ отсюда — заменить найденное X2-X \ Получите уравнение для прямой, которая проходит через значения k, точек M \ и M ^ в уравнении (5). L = (б) 2 / 2-2 / 1- Для этого уравнения Xi × X2, Y \ Φy-X2 = xi прямая, проходящая через точки M \ {xi ‘} yi) и M2 (x2] Y2), предполагается параллельной оси ординат. Форма уравнения: х = х . Если y2 = 2 / s, уравнение линии можно записать в виде y = y / i. Линия M-yM2 параллельна горизонтальной оси.
Уравнение отрезка Линия пересекает ось Ox в точке M \ (a; 0) и ось Oy в точке Mg (0; b). В этом случае уравнение (6) принимает следующий вид: U- 0 Это 6-0 0-а ‘ Это уравнение называется линейным сегментным уравнением. Это связано с тем, что числа a и b указывают, какой отрезок отрезает линия по координатным осям. , х-а Х у ~ + I = L a b в Mg (0; 6) б \ ИЛИ ®
Уравнение прямой через заданную точку, перпендикулярную этому вектору Найти линейное уравнение через заданную точку M0 (x0 \ y0), перпендикулярную данному ненулевому вектору n = (A; B). Возьмем произвольную точку M (x; y) на прямой и рассмотрим вектор M0M- (x-x0; Y-Yo). • Векторы n и McM являются вертикальными, поэтому их скалярное произведение равно нулю. A (x-x0) + B (y-yo) = 0. (7) Уравнение (7) называется уравнением прямой, проходящей через данную точку, перпендикулярную данному вектору и y. Вектор ri = (A) B), перпендикулярный прямой, называется вектором нормали этой прямой.
Уравнение (7) можно переписать в следующем формате Ax + By + C = 0, (8) Где A и B — координаты нормального вектора, а C = —Aho — W / o — свободный член. Уравнение (8) является общим уравнением для линии (см. (3)). 7. Полярные координатные уравнения для прямых Найти линейные уравнения в полярных координатах. Его положение может быть определено путем указания расстояния p от полюса O до конкретной линии и угла a между полюсом OP и осью I через полюс O, перпендикулярный этой линии. Для любой точки M (r; <p) на данной прямой: npj OM = p.
с другой стороны, pR / OM = \ OM \ cos (a- <p) = r • cos (<£ -a). так r cos (<^ — a) = p (9) Полученное уравнение (9) представляет собой линейное уравнение в полярных координатах. Линия нормального уравнения По заданным p и a определите линию (см. Рисунок). Рассмотрим декартову систему координат Оху. Вводит полярную систему координат с O в качестве полюса и Ox в качестве полярной оси. Уравнение линии можно записать в виде r-cos (y? -a) -p = 0, т.е. g • cos 9 cos и 4-g sin? грех: -p = 0. Однако уравнения, связанные с декартовой и полярной координатами, дают r cos) = x, rsinip = y.
Следовательно, линейное уравнение (9) в декартовой системе координат принимает вид: x-cosо4-у • sinа-р = 0. (10) Уравнение (10) называется линейным нормальным уравнением. 44 года п / / a \ x о Вот как можно сделать уравнение (3) прямой в виде (10). Умножим все слагаемые в уравнении (3) на некоторый коэффициент, чтобы получить Л ^ ОХЛх + ХВу + АС = 0. Это уравнение становится уравнением (10). В результате должно быть выполнено уравнение: A / 4 = cos a-, XB = sin a, A C = -p. Из первых двух уравнений найдите Л2А2 + A2J52 = cos2 a + sin2а, т.е. А = ±> * y / A2 + B’2 Х называется нормировочным фактором. Согласно третьему уравнению АС = -р, знак нормировочного коэффициента меняется на противоположный
