Оглавление:



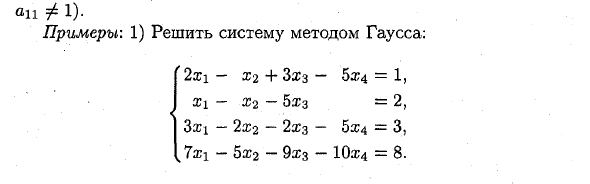


Решение систем линейных уравнений методом Гаусса
- Решение системы линейных уравнений Метод Гаусса (1) Одним из наиболее универсальных и эффективных методов решения систем линейной алгебры является метод Гаусса. Дайте одновременные уравнения (A \ X \ + a \ 2×2 + •• + a \ nxn = bu 1 a2 \ Xi 4-a22 ^ 2 + •• + a2nxn = b2 » «BAmnXn = b Гауссовский процесс принятия решения состоит из двух этапов.
. Следующая система является постепенной Гай си + a12x2 H —— б ахкк. -I —— b ainxn = b «22 ^ 2 + ‘•’ + & 2kXk H —— b 0-2n £ n = & 2> Я akkXk +; •• + akpn = bk, Здесь k ^ n, anφ0, i = 1, k. Коэффициент ats называется основным элементом системы. На втором этапе (обратный) неизвестные из этой системы шагов определяются последовательно. Я объясню метод Гаусса в деталях. Двигайся прямо.
На первом этапе (прямой ход) система сводится к постепенной (особенно треугольной) форме Людмила Фирмаль
Предположим, что основным элементом является otsΦ0 (если a = 0, мы впервые написали уравнение в системе, где коэффициент x \ не равен нулю). Преобразуйте систему (1), удалив неизвестные x \ во всех уравнениях, кроме первого (используя базовое преобразование системы).
Для этого умножим обе части первого уравнения на Добавьте термин для каждого члена во второе уравнение системы. Затем умножьте с обеих сторон первое уравнение и добавьте к третьему уравнению Емкость системы. Если вы продолжите этот процесс, вы получите эквивалент Система на ^ i + ai2X2 H —— h alnxn = bi a22 x2 t ‘• * T a2n xn- » am2®2 + •• + GmUn = bn • Где (t, j = 2, m) — новое значение коэффициента, Правильная часть получена после первого шага. Аналогичным образом исключают неизвестные X2 из всех уравнений системы, учитывая основной элемент <4UФ0, исключая первое и второе.
| Степенные ряды | Системы линейных однородных уравнений |
| Приложение рядов к приближенным вычислениям | Векторы и линейные операции над ними |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Продолжайте этот процесс как можно больше. Если процесс приведения системы (1) к постепенной форме показывает нулевые уравнения, то есть уравнения вида 0 = 0, они отбрасываются. Если отображается уравнение вида 0 = aΦ0>, это указывает на несовместимость системы. Второй шаг (обратный) — это решение ступенчатой системы. В общем, существует множество решений системы градуированных уравнений. В последнем уравнении этой системы первое неизвестное xb представлено оставшимися неизвестными (£ fc + 1, …, xn). Затем подставьте значение Xk в предпоследнее уравнение системы и выразите Xk- \ через a: n).
Тогда найди Xk-2> … Примечания: 1. Если система ступеней представляет собой треугольник, то есть k = 7i, исходная система имеет единственное решение. Найти xn из последнего уравнения и из второго уравнения xn-1) из последнего далее в систему всех остальных неизвестных [xn — 2? ••• yXi). 2.
Прибавьте произвольные значения к свободным неизвестным …, xn), получите бесконечное число решений для системы. Людмила Фирмаль
На практике удобнее выполнять все базовые преобразования для строк, используя матрицу расширения, а не систему (1). Удобно, если коэффициент aj равен 1 (переместить уравнение на место или отделить обе стороны уравнения все ф 1). Пример: 1) Решить систему, используя метод Гаусса. 2x \ -x-2 + 3×3-5 # 4 = 1, X \ -X2-bx3 = 2 3xi-2×2-2hz-5×4 = 3, 7xi-5×2-9hz-10×4 = 8.
♦ В результате базового преобразования в расширенную матрицу системы / 2-1 3 «-5 1 \ 1-1-5 0 2 3 -2 -2 -5 3 \ 7-5-9-10 8 / 1 -1 -5 0 2 \ 0 1 13 -5 -3 0 1 13 -5 -3 х0 2 26-10-6 / ^ 1 -1 -5 0 2 \ 2-13 -5 1 3 -2 -2 -5 3 ^ 7-5-9-10 8J -1 О 1 Ах ах \ 0 O -5 0 ‘2 л 13-5-3 LLC O O O y Оригинальная система была уменьшена до ступенчатой системы. xi-x2-5xs = 2 x2 + 13 Гц + 5×4 = -3. Итак, общее решение системы: x2 = -5×4-13x-X \ = -5×4-8×3-1. 1, x2 = x3 = 0, x4 = 0. 2) Решить систему, используя метод Гаусса. — = О, -3, ♦ X1 + x2 + x3 = 3, 2xi + 3×2 + 3×3 = 7, 3X] + X2 + x3 = 5, 5xi-x2-. Xs = 3. ♦ Выполнять базовые преобразования в строках расширенной матрицы системы.
/ 11 1 3 \ / 11 1 3 \ / 1 1 1 3 \ / 1 1 1 3 \ 2337 010 1 0101 0101 31 15 ~ 0-2—2-4 ~ 0112 ~ 0011 \ 5 -1 -1 3 / \ 0 -b -6 -12 / \ 0 I 1 2 / \ 0 0 0 0 / Полученная матрица соответствует системе + X-2 + xs = 3, X-2 = 1 Xb = 1. Выполнение обратного хода приводит к £ 3 = 1, x2-1, Xj = 1.
