Оглавление:
Задачи с целочисленными неизвестными отличаются тем, что в ответе должны получиться целые числа. Либо это оговаривается в условии, либо соответствует смыслу задачи. При этом задача может не иметь общего однозначного решения и только то, что ответ должен быть целочисленным, помогает найти окончательное решение. Чаще всего при решении таких задач используется свойство делимости, т.е. если при делении одного выражения на другое должно получиться целое число, то приходится подбирать такие значения неизвестных, которые обеспечивают деление без остатка.
Задача №20
Найдите все пары натуральных чисел, разность квадратов которых равна 55.
Решение:
По условию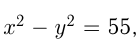 
где 
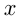и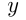 
— искомые числа,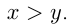
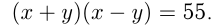
Число 55 может быть представлено в виде двух сомножителей: либо как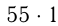 
, либо как 
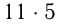, других возможностей нет. Т.к. 
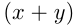— натуральное число и 
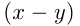— натуральное, то рассматриваются два случая:
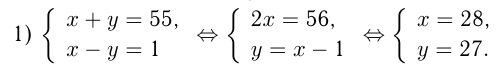
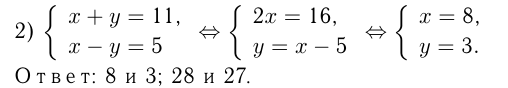
Задача №21
В автогонках принимают участие команды, имеющие одинаковое число автомобилей марк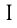и 
и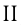 
, причем в каждой команде число всех автомобилей меньше 7. Если в каждой команде число автомобилей марки 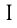оставить без изменения, а число автомобилей марки 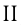увеличить в 3 раза, то общее число автомобилей марки 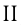, участвующих в гонках, будет на 50 больше общего числа автомобилей марки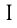, а число автомобилей в каждой команде превысит 12. Определить число команд, участвующих в гонках, и число автомобилей марк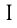и и 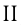в каждой команде.
Решение:
Обозначим число команд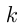 
, а число автомобилей марк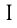и и 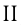в каждой команде — 
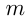и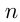 
соответственно. Условия задачи приводим к соотношениям:
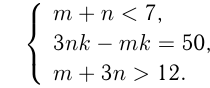
Займемся сначала неравенствами.
Из 1-го неравенства и условия задачи получаем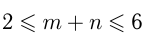 
и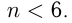 
3-е неравенство запишем в виде:
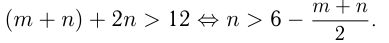
С учетом предыдущих неравенств получаем из последнего неравенства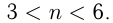 
Следовательно, 
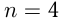или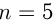 
.
Рассмотрим возможные случаи:
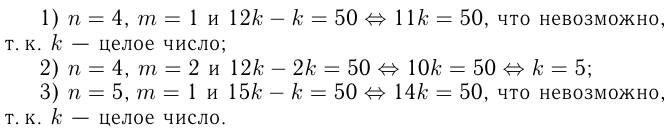
Итак, единственно возможный 2-й случай.
Ответ: число команд 5, в командах 2 автомобиля марки 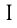и 4 автомобиля марки .
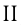Последний пример иллюстрирует не только решение задачи с целыми числами, но использование неравенств в условии и решении задачи.
Задача №22
Было куплено несколько одинаковых тетрадей и одинаковых книг, причем книг куплено на 4 больше, чем тетрадей. За все тетради заплачено 7 руб. 20 коп., за все книги 66 рублей. Если бы тетрадь стоила столько, сколько стоит книга, а книга — столько, сколько стоит тетрадь, то было бы истрачено меньше, чем 44 руб. 40 коп. Сколько куплено тетрадей?
Решение:
Пусть куплено 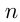книг и 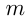тетрадей; книга стоит 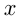руб., тетрадь — 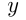руб. Тогда, исходя из условий, можно написать:
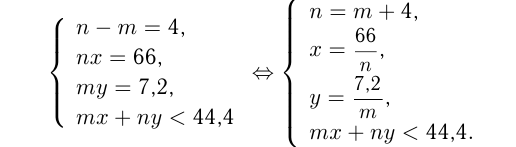
Подставим 3 первых равенства в неравенство:
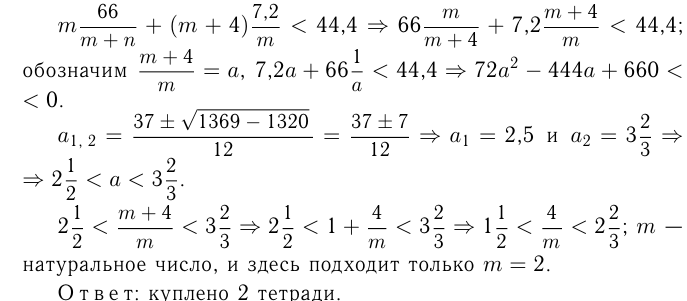
Задача №115
Некто купил 30 птиц за 30 монет. Из числа этих птиц за 3-х воробьев заплачена 1 монета, за 2-х горлиц — 1 монета, а за каждого голубя — 2 монеты. Сколько было куплено птиц каждой породы?
Решение:
Пусть куплено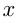 
воробьев, 
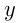горлиц, 
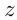голубей. Из условия 1 воробей стоит 
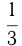монеты, 1 горлица — 
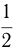монеты, 1 голубь — 2 монеты. Поэтому имеем 2 уравнения:
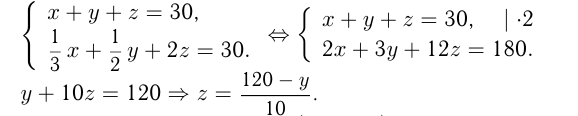
Т.к. 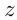— целое число, то 
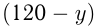должно делиться на 
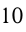, и, значит, 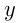либо 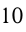, либо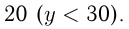 
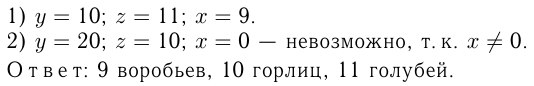
Задача №116
Вася и Петя поделили между собой 39 орехов. Число орехов, доставшихся любому из них, меньше удвоенного числа орехов, доставшихся другому. Квадрат трети числа орехов, доставшихся Пете, меньше увеличенного на 1 числа орехов, доставшихся Васе. Сколько орехов у каждого?
Решение:
Если у Васи 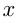орехов, а у Пети 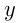орехов, то имеем систему:
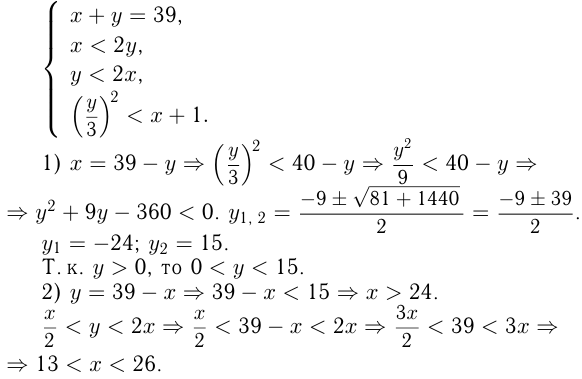
Отсюда, т. к.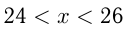 
и 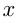— целое число, то 
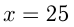и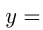 
Ответ: у Васи 25 орехов, у Пети 14 орехов.
Задача №117
Около дома посажены липы и березы, причем их общее количество более 14. Если увеличить вдвое количество лип, а количество берез увеличить на 18, то берез станет больше, чем лип. Если увеличить вдвое количество берез, не изменяя количества лип, то лип все равно будет больше, чем берез. Сколько лип и сколько берез было посажено?
Решение:
Если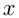 
— количество лип, а 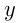— берез, то, исходя из условий, получаем:
Задача №118
Группа студентов, состоящая из 30 человек, получила на экзамене оценки 2, 3, 4 и 5. Сумма полученных оценок равна 93, причем «троек» было больше, чем «пятерок», и меньше, чем «четверок». Кроме того, число «четверок» делится на 10, а число «пятерок» — четное. Определить, сколько каких оценок получила группа.
Решение:
Пусть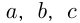 
и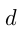 
— числа «двоек», «троек», «четверок» и «пятерок» соответственно.
Из условий имеем:
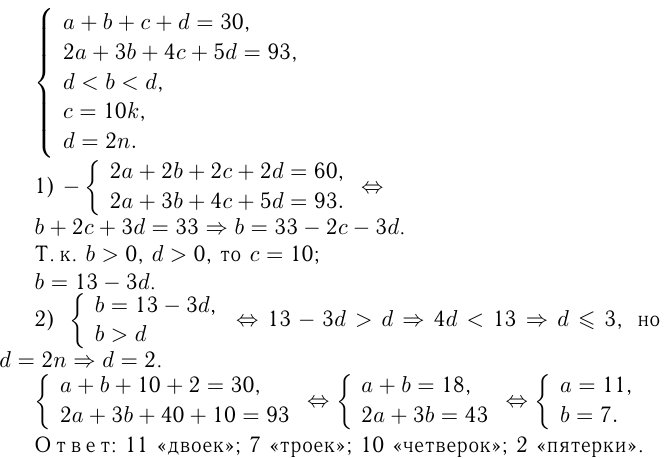
Задача №119
Четыре школьника сделали в магазине канцтоваров следующие покупки: 1-й купил пенал и ластик за 40 руб., 2-й купил ластик и карандаш за 12 руб., 3-й купил пенал, карандаш и 2 тетради за 50 руб., 4-й купил пенал и тетрадь. Сколько заплатил 4-й школьник?
Решение:
Обозначим стоимость товаров:
По условию:
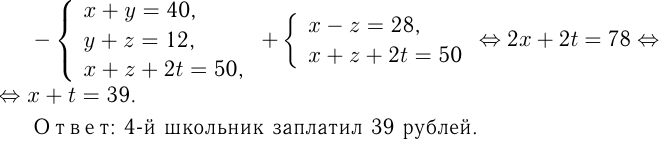
Задача №120
Рота солдат прибыла на парад в полном составе прямоугольным строем по 24 человека в ряд. По прибытии оказалось, что не все солдаты могут участвовать в параде. Оставшийся для парада состав роты перестроили так, что число рядов стало на 2 меньше прежнего, а число солдат в каждом ряду стало на 26 больше числа новых рядов. Известно, что если бы все солдаты участвовали в параде, то роту можно было бы выстроить так, чтобы число солдат в каждом ряду равнялось числу рядов. Сколько солдат было в роте?
Решение:
Допустим, в строю солдат было 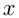рядов, тогда солдат было 
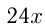человек. На параде число рядов стало 
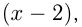а солдат в ряду 
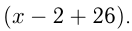Известно, что
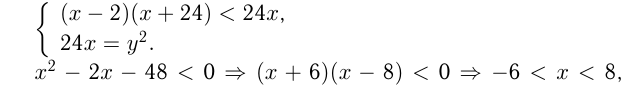
но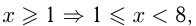 
т. е. 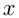может равняться одному из чисел: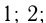
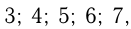но 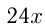должно быть полным квадратом. Проверяя, получим, что только 
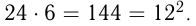Поэтому 
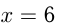.Ответ: в роте было 144 человека.
Задача №121
На заводе было несколько одинаковых прессов, штампующих детали, и завод выпускал 6480 деталей в день. После реконструкции все прессы заменили на более производительные, но также одинаковые, а их количество увеличилось на 3. Завод стал выпускать в день 11200 деталей. Сколько прессов было первоначально?
Решение:
Пусть было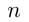 
прессов и стало 
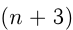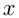; и 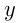дет./дн. — старая и новая производительности прессов; 
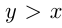. Тогда можно записать:
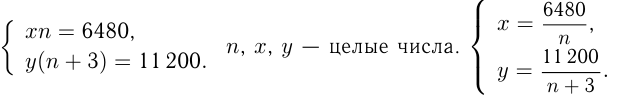
Если 6480 делится на 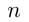, то 11 200 делится на 
.
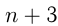Разложим числа 6480 и 11 200 на множители:
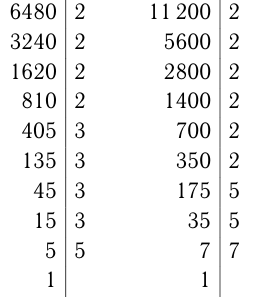
Будем подбирать возможные делители для 6480 и 11 200.
Задача №122
Производительность 1-го автомобильного завода не превышает 950 машин в сутки. Производительность 2-го автомобильного завода первоначально составляла 95% от производительности 1-го. После ввода дополнительной линии 2-й завод увеличил производство машин в сутки на 23% от числа машин, выпускаемых в сутки на 1-м заводе, и стал их выпускать более 1000 штук в сутки. Сколько автомобилей за сутки выпускал каждый завод до реконструкции 2-го завода? Предполагается, что каждый завод в сутки выпускает целое количество машин.
Решение:
Пусть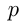 
— производительность 1-го завода и 
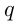маш./сут. — производительность 2-го завода до реконструкции. Тогда
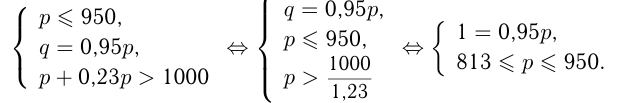
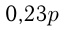и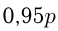 
должны быть целыми числами;
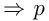должно делиться на 
;
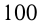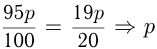должно делиться на 
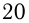. Если 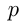делится на 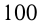, то оно делится и на 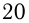. Поэтому 
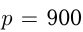и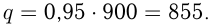 
Ответ: 900 машин в сутки и 855 машин в сутки.
Задача №123
Трое мальчиков хотели вместе купить две одинаковые игрушки. Сложив все имеющиеся у них деньги, дети не могли купить даже одну игрушку. Если бы у 1-го мальчика было вдвое больше денег, то им на покупку 2-х игрушек не хватило бы 34 руб. Когда 3-му мальчику добавили денег в размере в 2 раза большем, чем у него было, то после покупки игрушек у детей оставалось 6 руб. Сколько стоили игрушки, если первоначально у 2-го мальчика было на 9 руб. больше, чем у 1-го?
Решение:
Пусть у мальчиков было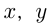
и 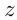руб., а одна игрушка стоила 
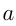руб. Тогда условия дают нам систему:
Задача №124
Строительная бригада состоит из 32 человек, каждый из которых владеет одной или двумя строительными профессиями: каменщик, бетонщик, плотник. Людей, владеющих профессией плотника, в бригаде в 2 раза больше, чем людей, владеющих профессией бетонщика, и в 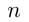раз меньше, чем людей, владеющих профессией каменщика, причем 
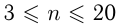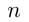( — целое число). Сколько человек в бригаде владеет только одной профессией, если число людей, владеющих двумя профессиями, на 2 больше, чем число людей, владеющих профессией плотника?
Решение:
Обозначим: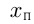
— количество плотников; 
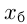— количество бетонщиков; 
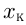— количество каменщиков; 
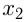— число людей, владеющих 2-мя профессиями; 
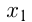— число людей, владеющих одной профессией. Из условий:
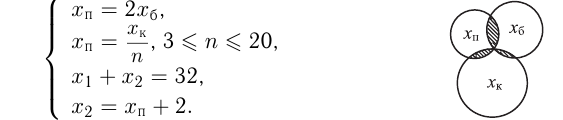
Изобразим множества плотников, бетонщиков и каменщиков в виде пересекающихся кругов, где общие части кругов — это люди, владеющие какими-то 2-мя профессиями.
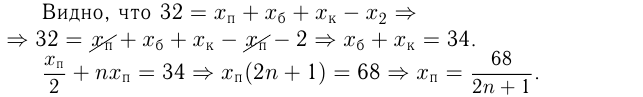
Т. к. 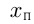— целое число, 68 должно делиться на нечетное число 
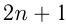, где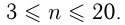 
Нетрудно догадаться, что
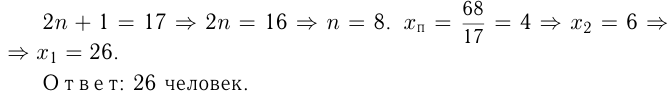
Задача №125
Две бригады землекопов вырыли по одинаковому котловану, причем 2-я бригада работала на полчаса больше 1-й. Если бы в 1-й бригаде было на 5 человек больше, то она могла бы закончить работу на 2 часа раньше. Определить число землекопов в каждой бригаде, если производительность у них одинакова.
Решение:
Пусть в 1-й бригаде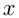, а во 2-й — 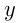человек; 1-я бригада работала 
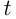, тогда 2-я брагада работала 
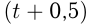часов. Условия задачи приводят к системе:
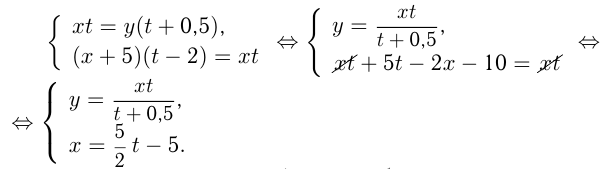
Т. к. 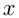— целое число, 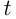должно быть целым, четным и 
.
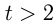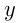— также целое число.
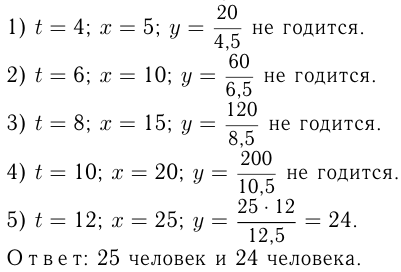
Задача №126
Три комбайна разной производительности убрали урожай с участка за 1 ч 12 мин. За сколько часов убрал бы урожай каждый из них в отдельности, если известно, что это это число часов целое (для каждого комбайна)?
Решение:
Пусть площадь участк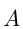а 
га,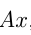 
, 
, 
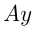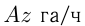— производительности комбайнов, где 
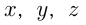— части участка, убираемые за 1 час. 
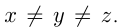Тогда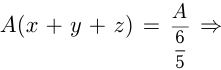 
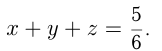
Если бы комбайны работали отдельно, то 1-й комбайн убрал бы урожай за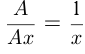 
, 2-й комбайн — за 
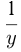, 3-й — за 
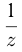ч., где 
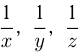— целые числа. Значит, 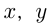и 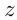— дроби, у которых в числителе 1.
Нужно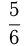 
— представить в виде суммы трех таких дробей.
Допустим,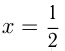 
, тогда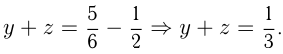 
Допустим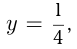 
тогда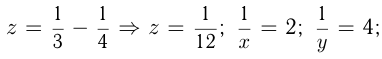 
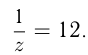
Ответ: 2 часа, 4 часа и 12 часов.
Задача №127
Найти все натуральные трехзначные числа, каждое из которых обладает следующими двумя свойствами:1) первая цифра числа в 3 раза меньше последней его цифры;2) сумма самого числа с числом, получающимся из него перестановкой второй и третьей его цифр, делится на 8 без остатка.
Решение:
Имеем число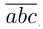 
, т. е. 
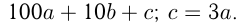По условию
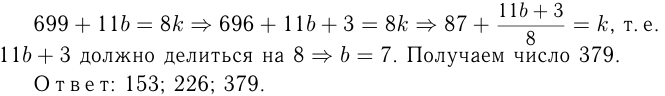
Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Решение задач на части по математике |
| Решение задач на числа по математике |
| Решение задач с помощью неравенств |
| Решение задач на прогрессии по математике |
