Ряды Тейлора и Маклорена
Для приложений важно уметь данную функцию  разлагать в степенной ряд, т. е. функцию
разлагать в степенной ряд, т. е. функцию  представлять в виде суммы степенного ряда.
представлять в виде суммы степенного ряда.
Как известно (см. теорема 26.1), для любой функции  , определенной в окрестности точки
, определенной в окрестности точки 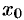 и имеющей в ней производные до
и имеющей в ней производные до 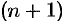 -го порядка включительно, справедлива формула Тейлора:
-го порядка включительно, справедлива формула Тейлора:
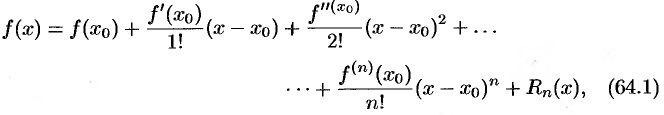
где 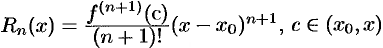 , — остаточный член в форме Лагранжа. Число
, — остаточный член в форме Лагранжа. Число 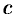 можно записать в виде
можно записать в виде 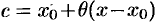 , где
, где 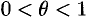 . Формулу (64.1) кратко можно записать в виде
. Формулу (64.1) кратко можно записать в виде
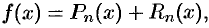
где 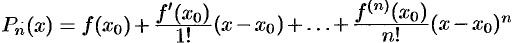 — многочлен Тейлора.
— многочлен Тейлора.
Если функция  имеет производные любых порядков (т. е. бесконечно дифференцируема) в окрестности точки
имеет производные любых порядков (т. е. бесконечно дифференцируема) в окрестности точки 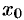 и остаточный член
и остаточный член 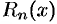 стремится к нулю при
стремится к нулю при 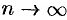 (
( 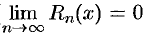 ), то из формулы Тейлора получается разложение функции
), то из формулы Тейлора получается разложение функции  по степеням (
по степеням (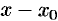 ), называемое рядом Тейлора:
), называемое рядом Тейлора:

Если в ряде Тейлора положить 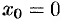 , то получим разложение функции по степеням
, то получим разложение функции по степеням  в так называемый ряд Маклорена:
в так называемый ряд Маклорена:
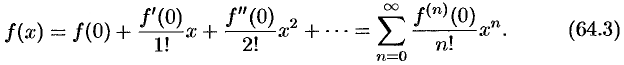
Отметим, что ряд Тейлора можно формально построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки 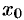 . Но отсюда еще не следует, что он будет сходиться к данной функции
. Но отсюда еще не следует, что он будет сходиться к данной функции  ; он может оказаться расходящимся или сходиться, но не к функции
; он может оказаться расходящимся или сходиться, но не к функции  . Так, например, функция
. Так, например, функция
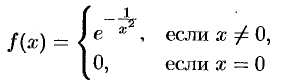
имеет в точке 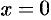 производные всех порядков, причем
производные всех порядков, причем 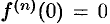 при всяком
при всяком  (см. пример 19.5). Ряд Маклорена имеет вид
(см. пример 19.5). Ряд Маклорена имеет вид
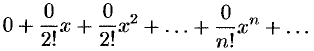
Он сходится, но его сумма 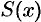 в любой точке
в любой точке  равна нулю, а не
равна нулю, а не  .
.
Пусть для функции  составлен соответствующий ей ряд Тейлора.
составлен соответствующий ей ряд Тейлора.
Теорема 64.1. Для того чтобы ряд Тейлора (64.2) функции  сходился к
сходился к  в точке
в точке  , необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (64.1) стремился к нулю при
, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (64.1) стремился к нулю при 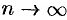 , т. е. чтобы
, т. е. чтобы 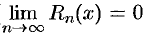 .
.
Пусть ряд Тейлора (64.2) сходится к функции  в некоторой окрестности точки
в некоторой окрестности точки 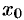 , т. е.
, т. е.  . Так как
. Так как  -я частичная сумма
-я частичная сумма 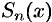 ряда (64.2) совпадает с многочленом Тейлора
ряда (64.2) совпадает с многочленом Тейлора 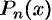 , т. е.
, т. е.  , находим:
, находим:
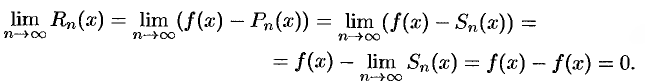
Обратно, пусть 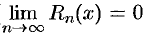 . Тогда
. Тогда
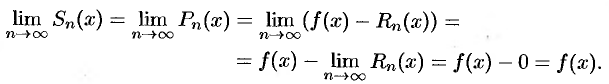
Замечание.. Если ряд Тейлора (64.2) сходится к порождающей функции  , то остаточный член формулы Тейлора равен остатку ряда Тейлора, т. е.
, то остаточный член формулы Тейлора равен остатку ряда Тейлора, т. е. 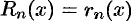 . (Напомним, что
. (Напомним, что 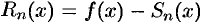 , а
, а 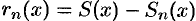 , где
, где 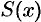 — сумма ряда Тейлора.)
— сумма ряда Тейлора.)
Таким образом, задача разложения функции  в степенной ряд сведена по существу к определению значений
в степенной ряд сведена по существу к определению значений  , при которых
, при которых 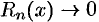 (при
(при 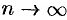 ). Если сделать это не просто, то следует каким-нибудь иным способом убедиться, что написанный ряд Тейлора сходится к данной функции.
). Если сделать это не просто, то следует каким-нибудь иным способом убедиться, что написанный ряд Тейлора сходится к данной функции.
На практике часто пользуются следующей теоремой, которая дает простое достаточное условие разложимости функции и ряд Тейлора.
Теорема 64.2. Если модули всех производных функций  ограничены в окрестности точки
ограничены в окрестности точки 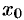 одним и тем же числом
одним и тем же числом 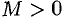 , то для любого
, то для любого  из этой окрестности ряд Тейлора функции
из этой окрестности ряд Тейлора функции  сходится к функции
сходится к функции  , т. е. имеет место разложение (64.2).
, т. е. имеет место разложение (64.2).
Согласно теореме 64.1, достаточно показать, что 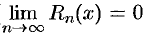 . По условию теоремы 64.2 для любого
. По условию теоремы 64.2 для любого  имеет место неравенство
имеет место неравенство 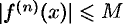 . Тогда имеем:
. Тогда имеем:
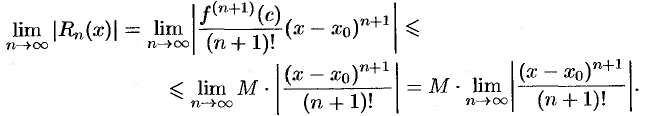
Осталось показать, что 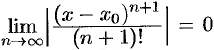 . Для этого рассмотрим ряд
. Для этого рассмотрим ряд
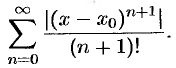
Так как
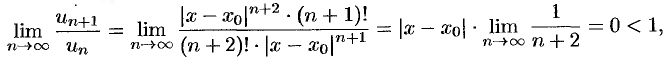
то по признаку Даламбера этот ряд сходится на всей числовой оси. Но тогда, в силу необходимого признака сходимости,
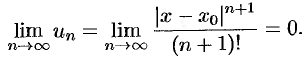
Следовательно, 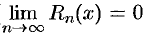 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Сходимость степенных рядов |
| Свойства степенных рядов |
| Периодические функции. Периодические процессы |
| Разложение в ряд фурье периодических функций с периодом 2п |
