Оглавление:
Сходимость степенных рядов
Выясним вопрос о сходимости степенного ряда (62.3).
Область сходимости степенного ряда (62.3) содержит по крайней мере одну точку: 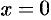 (ряд (62.4) сходится в точке
(ряд (62.4) сходится в точке 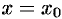 ).
).
Теорема Н. Абеля
Об области сходимости степенного ряда можно судить, исходя из следующей теоремы.
Теорема 63.1 (Абель). Если степенной ряд (62.3) сходится при 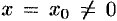 , то он абсолютно сходится при всех значениях
, то он абсолютно сходится при всех значениях  , удовлетворяющих неравенству
, удовлетворяющих неравенству 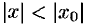 .
.
По условию ряд 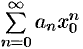 сходится. Следовательно, по необходимому признаку сходимости
сходится. Следовательно, по необходимому признаку сходимости 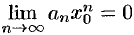 . Отсюда следует, что величина
. Отсюда следует, что величина 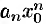 ограничена, т. е. найдется такое число
ограничена, т. е. найдется такое число 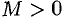 , что для всех
, что для всех  выполняется неравенство
выполняется неравенство 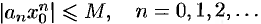
Пусть 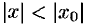 , тогда величина
, тогда величина 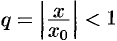 и, следовательно,
и, следовательно,
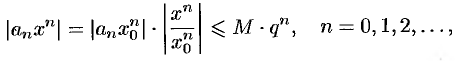
т. е. модуль каждого члена ряда (62.3) не превосходит соответствующего члена сходящегося (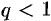 ) ряда геометрической прогрессии. Поэтому по признаку сравнения при
) ряда геометрической прогрессии. Поэтому по признаку сравнения при 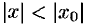 ряд (62.3) абсолютно сходящийся.
ряд (62.3) абсолютно сходящийся.
Следствие 63.1. Если ряд (62.3) расходится при 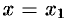 , то он расходится и при всех
, то он расходится и при всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству 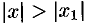 .
.
Действительно, если допустить сходимость ряда в точке 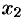 , для которой
, для которой 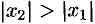 , то по теореме Абеля ряд сходится при всех
, то по теореме Абеля ряд сходится при всех  , для которых
, для которых 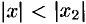 , и, в частности, в точке
, и, в частности, в точке 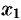 , что противоречит условию.
, что противоречит условию.
Интервал и радиус сходимости степенного ряда
Из теоремы Абеля следует, что если 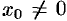 есть точка сходимости степенного ряда, то интервал
есть точка сходимости степенного ряда, то интервал 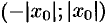 весь состоит из точек сходимости данного ряда; при всех значениях
весь состоит из точек сходимости данного ряда; при всех значениях  вне этого интервала ряд (62.3) расходится.
вне этого интервала ряд (62.3) расходится.

Интервал 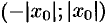 и называют интервалом сходимости степенного ряда. Положив
и называют интервалом сходимости степенного ряда. Положив 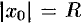 , интервал сходимости можно записать в виде
, интервал сходимости можно записать в виде 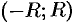 . Число
. Число 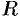 называют радиусом сходимости степенного ряда, т. е.
называют радиусом сходимости степенного ряда, т. е. 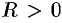 — это такое число, что при всех
— это такое число, что при всех  , для которых
, для которых 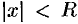 , ряд (62.3) абсолютно сходится, а при
, ряд (62.3) абсолютно сходится, а при 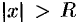 ряд расходится (см. рис. 259).
ряд расходится (см. рис. 259).
В частности, когда ряд (62.3) сходится лишь в одной точке 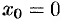 , то считаем, что
, то считаем, что 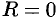 . Если же ряд (62.3) сходится при всех значениях
. Если же ряд (62.3) сходится при всех значениях 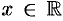 (т. е. во всех точках числовой оси), то считаем, что
(т. е. во всех точках числовой оси), то считаем, что 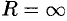 .
.
Отметим, что на концах интервала сходимости (т. е. при 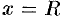 и при
и при 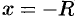 ) сходимость ряда проверяется в каждом случае отдельно.
) сходимость ряда проверяется в каждом случае отдельно.
Для нахождения радиуса сходимости степенного ряда (62.3) можно поступить следующим образом. Составим ряд из модулей членов данного степенного ряда
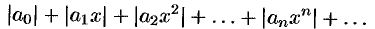
Я и применим к нему признак Даламбера. Допустим, что существует предел
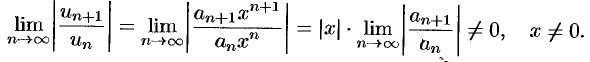
По признаку Даламбера ряд сходится, если 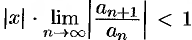 , т.е. ряд сходится при тех значениях
, т.е. ряд сходится при тех значениях  , для которых
, для которых
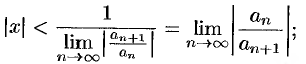
ряд, составленный из модулей членов ряда (62.3), расходится при тех значениях  , для которых
, для которых 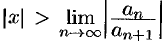 . Таким образом, для ряда (62.3) радиус абсолютной сходимости
. Таким образом, для ряда (62.3) радиус абсолютной сходимости

Аналогично, воспользовавшись радикальным признаком Коши, можно установить, что

Замечания.
- Если
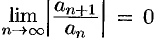 , то можно убедиться, что ряд (62.3) абсолютно сходится на всей числовой оси. В этом случае
, то можно убедиться, что ряд (62.3) абсолютно сходится на всей числовой оси. В этом случае 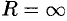 . Если
. Если 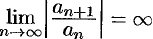 , то
, то 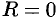 .
. - Интервал сходимости степенного ряда (62.4) находят из первенства
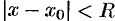 ; имеет вид
; имеет вид 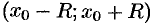 .
. - Если степенной ряд содержит не все степени
 , т. е. задан неполный степенной ряд, то интервал сходимости ряда находят без определения радиуса сходимости (формулы (63.1) и (63.2)), а непосредственно применяя признак Даламбера (или Коши) для ряда, составленного из модулей членов данного ряда.
, т. е. задан неполный степенной ряд, то интервал сходимости ряда находят без определения радиуса сходимости (формулы (63.1) и (63.2)), а непосредственно применяя признак Даламбера (или Коши) для ряда, составленного из модулей членов данного ряда.
Пример №63.1.
Найти область сходимости ряда 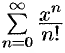 .
.
Решение:
Воспользуемся формулой (63.1):
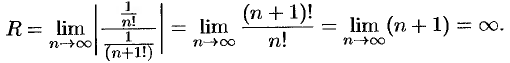
Следовательно, данный ряд абсолютно сходится на всей числовой оси.
Дополнительные примеры:
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Знакочередующиеся ряды. Признак Лейбница |
| Общий достаточный признак сходимости знакопеременных рядов |
| Свойства степенных рядов |
| Ряды Тейлора и Маклорена |
