Оглавление:
Задача 2.102.
Швейное предприятие планирует к массовому выпуску новую модель одежды. Спрос на эту модель не может быть точно определен. Однако можно предположить, что его величина характеризуется тремя возможными состояниями (I, II, III). С учетом этих состояний анализируются три возможных варианта выпуска данной модели (А,Б, В).
Каждый из этих вариантов требует своих затрат и обеспечивает в конечном счете различный эффект. Прибыль (тыс. руб.), которую получает предприятие при данном объеме выпуска модели и соответствующем состоянии спроса, определяется матрицей

Требуется найти объем выпуска модели одежды, обеспечивающий среднюю величину прибыли при любом состоянии спроса.
Решение:
Прежде всего проверим, имеет ли исходная матрица седловую точку. Для этого находим минимальные элементы в ее строках (22; 21; 20) и максимальные— в столбцах (22; 23; 24). Максимальным среди минимальных элементов строк является число 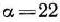 , а минимальным среди максимальных элементов столбцов — число
, а минимальным среди максимальных элементов столбцов — число 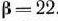 . Таким образом.
. Таким образом. 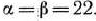 . Число 22 является ценой игры. Игра имеет седловую точку, соответствующую I варианту выпуска модели одежды. Объем выпуска модели, соответствующей данному варианту, обеспечивает прибыль в 22 тыс, руб. при любом состоянии спроса.
. Число 22 является ценой игры. Игра имеет седловую точку, соответствующую I варианту выпуска модели одежды. Объем выпуска модели, соответствующей данному варианту, обеспечивает прибыль в 22 тыс, руб. при любом состоянии спроса.
Используя геометрическую интерпретацию, найдите решение игр, определяемых следующими матрицами.
Сведение задач теории игр к задачам линейного программирования. Рассмотрим игру  , определяемую матрицей
, определяемую матрицей
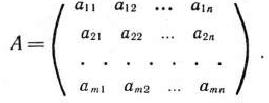
Согласно теореме 2.5, для оптимальной стратегии первого игрока
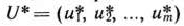
и цены игры 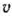 выполняется неравенство
выполняется неравенство
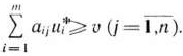
Предположим для определенности, что 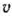 > 0. Это всегда может быть достигнуто благодаря тому, что прибавление ко всем элементам матрицы
> 0. Это всегда может быть достигнуто благодаря тому, что прибавление ко всем элементам матрицы 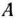 одного и того же. Постоянного числа
одного и того же. Постоянного числа 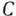 не приводит к изменению оптимальных стратегий, а только лишь увеличивает цену игры на
не приводит к изменению оптимальных стратегий, а только лишь увеличивает цену игры на 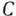 .
.
Разделив теперь обе части последнего неравенства на 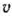 , получим
, получим
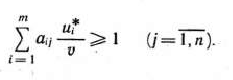
Положим

тогда
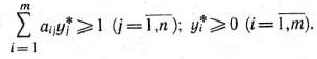
Используя введенное обозначение, перепишем условие
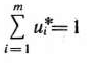
в виде
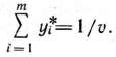
Так как первый игрок стремится получить максимальный выигрыш, то он должен обеспечить минимум величине 1/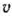 . С учетом этого, определение оптимальной стратегии первого игрока сводится к нахождению минимального значения функции
. С учетом этого, определение оптимальной стратегии первого игрока сводится к нахождению минимального значения функции
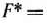
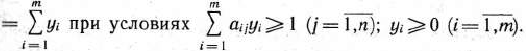
Аналогичные рассуждения показывают, что определение оптимальной стратегии второго игрока сводится к нахождению максимального значения функции
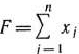
при условиях
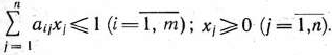
Здесь
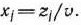
Таким образом, чтобы найти решение данной игры, определяемой матрицей А, нужно составить следующую пару двойственных задач и найти их решение.
Прямая задача: найти максимальное значение функции
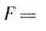
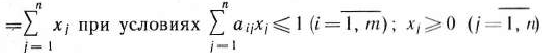
Двойственная задача: найти минимальное значение функции
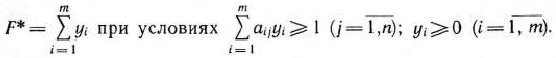
Используя решение пары двойственных задач, получаем формулы для определения стратегий и цены игры:
Итак, процесс нахождения решения игры с использованием методов линейного программирования включает следующие этапы:
- Составляют пару двойственных задач линейного программирования, эквивалентных данной матричной игре.
- Определяют оптимальные планы пары двойственных задач.
- Используя соотношение между планами пары двойственных задач и оптимальными стратегиями и ценой игры, находят решение игры.
Задача 2.106.
Найти решение игры, определяемой матрицей
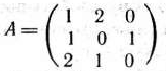
Решение:
Составим двойственную пару задач линейного программирования: прямая задача: найти максимум функции
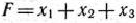
при условиях
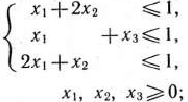
двойственная задача: найти минимум функции
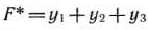
при условиях
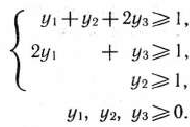
Находим оптимальные планы прямой и двойственной задач (табл. 2.52).
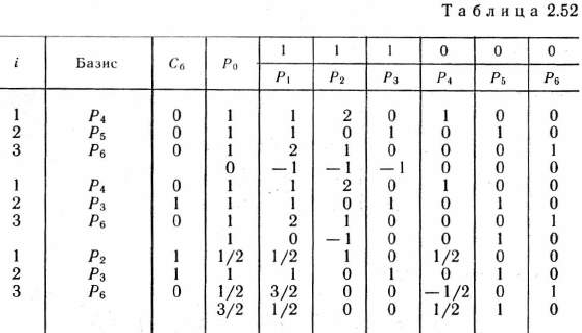
Из табл. 2.52 видно, что исходная задача имеет оптимальный план
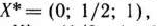
а двойственная задача — оптимальный план
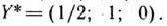
Следовательно, цена игры
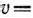
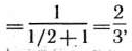
а оптимальные стратегии игроков
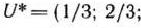
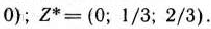
Выше было показано, что для всякой матричной игры можно записать симметричную пару двойственных задач, Справедливо и обратное: для всякой симметричной пары двойственных задач можно записать матричную игру.
Пусть задана симметричная пара двойственных задач: прямая задача:
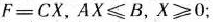
двойственная задача:
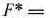
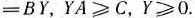
Тогда этой симметричной паре двойственных задач можно поставить в соответствие игру, определяемую матрицей
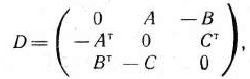
где индекс 1 означает операцию транспонирования.
Следует отметить, что если каждая матричная игра имеет оптимальные стратегии, то не всякая задача линейного программирования имеет решения.
Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:
