Оглавление:
Симметрические и кососимметрические уравнения
Симметрическим уравнением n -й степени называется алгебраическое уравнение вида
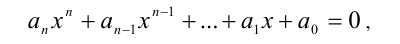
где равноотстоящие от концов многочлена коэффициенты равны, т.е.
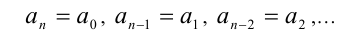
Рассмотрим отдельно решение симметрических уравнений чётной и нечётной степеней [30].
Если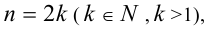 
то поделим уравнение на 
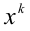и сделаем замену 
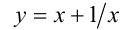. В результате получим алгебраическое уравнение степени в два раза ниже первоначальной, решив которое и сделав обратную подстановку, найдём все решения уравнения.
Если же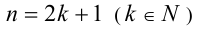 
, то одним из корней уравнения всегда будет x = — 1. Делением многочлена в левой части уравнения на x + 1 задача сводится к решению симметрического уравнения степени n = 2k , метод решения которого рассматривался выше.
Пример №189.
Решить уравнение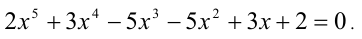 
Решение:
Очевидно, имеем симметрическое уравнение 5-й степени. Решаем его по изложенной выше схеме. Одним из корней уравнения будет число x = — 1. Найдём другие корни:
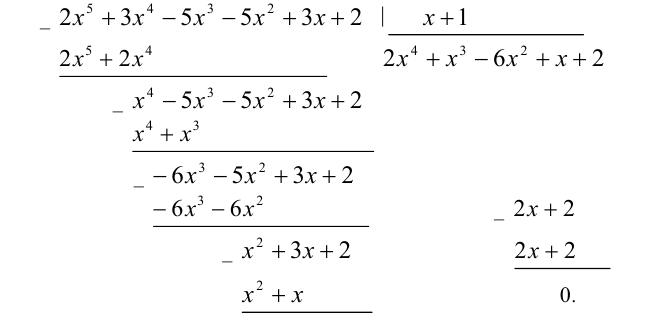
Решим симметрическое уравнение 4-й степени
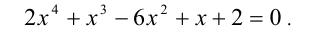
Поделим для этого обе части уравнения на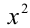 
:
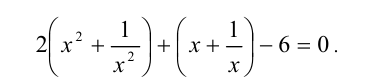
Обозначим у = x + (1/x), тогда
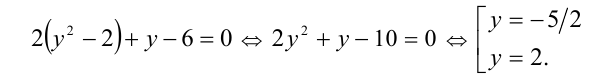
Выполняя обратную подстановку, получаем
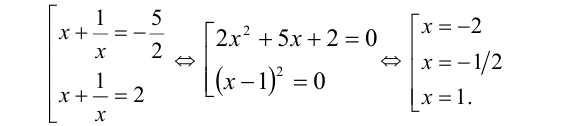
Объединяя полученные решения, приходим к ответу: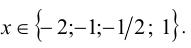 
Кососимметрическим уравнением n -й степени называется уравнение вида
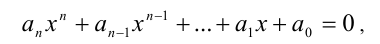
где равноотстоящие от концов многочлена коэффициенты являются противоположными числами, т.е.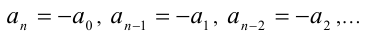 
Решение кососимметрических уравнений чётной и нечётной степени во многом аналогично решению соответствующих симметрических уравнений.
Если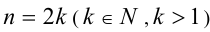 
, то делением обеих частей уравнения на 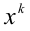и заменой 
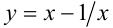получим алгебраическое уравнение степени в два раза ниже первоначальной, решив которое и сделав обратную подстановку, найдём решения уравнения.
Если же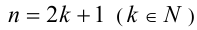 
, то одним из корней уравнения всегда будет x = 1, поэтому делением на x — 1 получаем кососимметрическое уравнение степени n = 2k . Задача свелась к предыдущей.
Пример №190.
Решить уравнение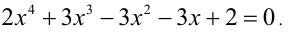 
Решение:
Это кососимметрическое уравнение 4-й степени. Поскольку x = 0 не является корнем уравнения, то поделим обе его части на :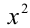
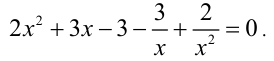
Перепишем последнее уравнение в виде
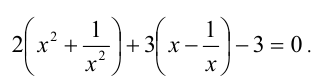
Положим у = х — (1/x), тогда получим
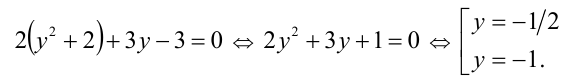
Выполняя обратную подстановку, получаем 4 решения
Пример №191.
Найти все значения параметра а , при которых уравнение
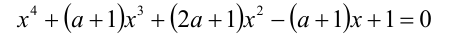
на промежутке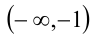 
имеет не менее двух корней.
Решение:
Так как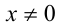 
, то делением уравнения на 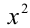, группировкой слагаемых с одинаковыми коэффициентами и заменой у = x — (1/х), получаем равносильное уравнение
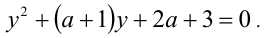
Поскольку функция у =x — (1/x) возрастает на промежутке 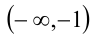от 
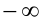до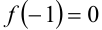 
, то исходное уравнение имеет не менее двух корней на 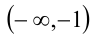тогда и только тогда, когда, когда полученное уравнение имеет два отрицательных корня 
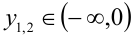т.е. когда
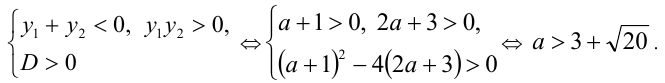
Ответ: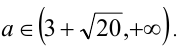 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
