Оглавление:
Системы линейных уравнений n*n
Система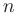 
линейных уравнений, содержащая 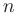неизвестных величин имеет вид
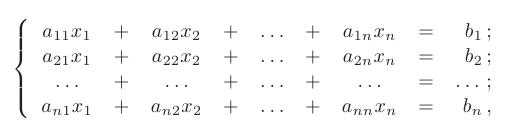
где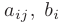 
— действительные числа, называемые коэффициентами при неизвестных 
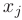и свободными членами уравнений соответсвенно. В более компактной форме эта система записывается:
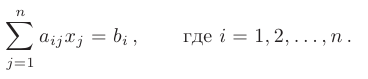
Система линейных уравнений называется однородной, если все ее свободные члены равны нулю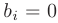 
.
Решением системы линейных уравнений называется такая упорядоченная совокупность значений переменных 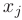, которая при подстановке в каждое из уравнение системы обращает его в верное равенство. Совместной называют систему уравнений, если она имеет хотя бы одно решение. Если система уравнений имеет единственное решение, то она называется определенной.
Используя правила действий над матрицами, вышеуказанную систему уравнений можно представить в виде
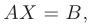
где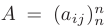 
— матрица коэффициентов системы; 
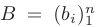-матрица-столбец свободных членов; 
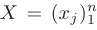— матрица-столбец искомых неизвестных величин.
Можно показать, что если матрица системы уравнений А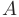
— невырожденная, то искомое решение может быть получено с помощью обратной матрицы коэффициентов системы:
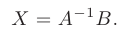
Пример:
Задана система линейных алгебраических уравнений:
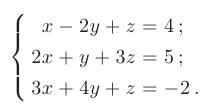
Требуется решить заданную систему уравнений с помощью обратной матрицы (матричным методом) и сделать проверку полученного решения.
► Обозначим матрицу коэффициентов системы, вектор правых частей и вектор неизвестных буквами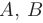 
и 
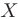соответственно:
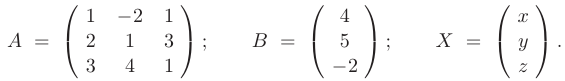
Тогда, учитывая свойства матриц, исходную систему уравнений можно записать в виде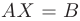 
, а ее решение как 
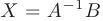, где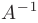 
-матрица, обратная к матрице коэффициентов системы 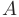, составляться из алгебраических дополнений по формуле, приведеной в п.1.4.:
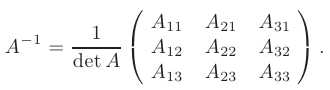
Вычислим алгебраические дополнения для всех элементов матрицы :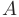
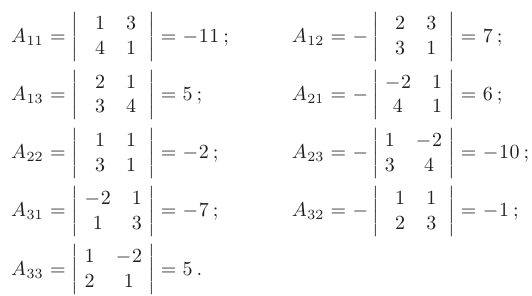
Для проверки правильности вычисления алгебраических дополнений вычислим определитель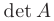 
путем его разложения по каждой строке:
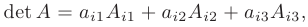
где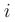 
= 1,2,3. Для 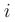= 1 имеем формулу
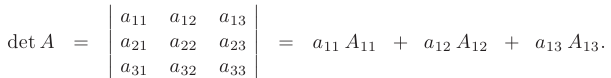
Т.е.
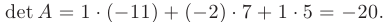
Аналогично с помощью разложения по 2-й и 3-й строкам вычисляем:
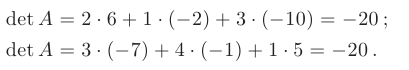
Так как все три определителя равны, то можно сделать вывод о правильности вычисления алгебраических дополнений.
Составим обратную матрицу и найдем искомое решение:
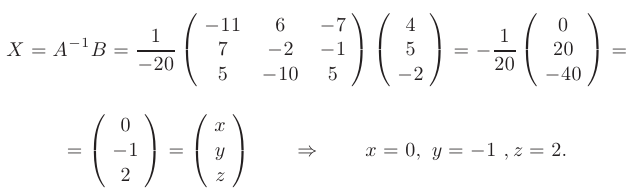
Для проверки подставим найденное решение в исходные уравнения системы:
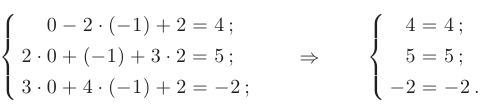
После подстановки получили верные тождества, следовательно, можно сделать вывод о правильности найденного решения.
Использование свойств определителей позволяет прийти к следующему утверждению, известному под названием теоремы Крамера.
Пусть 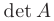— определитель матрицы коэффициентов 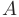системы линейных уравнений с 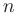неизвестными 
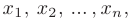a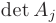 
-определитель матрицы, получаемой из 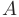при замене ее столбца коэффициентов при переменной 
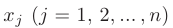на матрицу-столбец свободных членов 
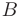. Если 
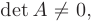, то исходная система уравнений имеет единственное решение, определяемое по формулам Крамера:
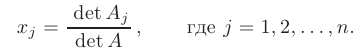
Заметим, что если определитель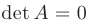 
и все дополнительные определители 
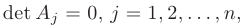то система уравнений имеет бесконечное множество решений. Если же определитель 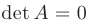и хотя бы один из определителей 
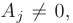то система уравнений несовместна.
Пример:
Решить систему уравнений из примера 1.1. методом Крамера.
► Т. к. согласно решению примера 1.1. определитель системы уравнений не равен нулю, то ее решение можно найти по формулам Крамера:
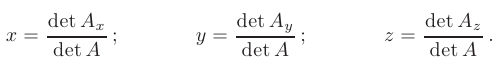
В нашем случае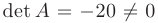 
и можно сделать вывод о том, что система имеет единственное решение. Для отыскания этого решения вычислим определители 
:
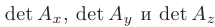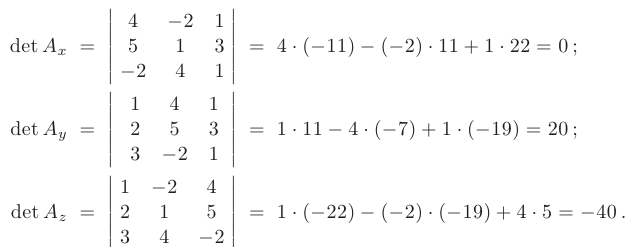
Воспользовавшись формулами Крамера, окончательно получим:
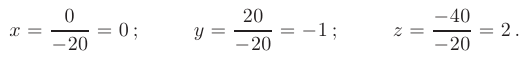
Пример:
Решить линейную систему уравнений из примера 1.1. методом Гаусса.
Составим расширенную матрицу системы:
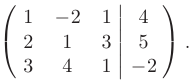
Прямой ход метода Гаусса. Приведем исходную систему уравнений к верхнему треугольному виду с помощью серии элементарных преобразований.
Вначале исключим переменную х из второго и третьего уравнений. Для этого первую строку расширенной матрицы умножим на —2 и почленно сложим со второй строкой, а затем первую строку расширенной матрицы умножим на —3 и почленно сложим с третьей строкой:
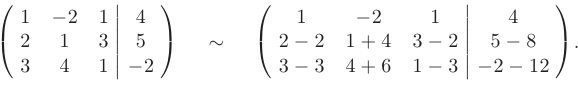
Теперь исключим переменную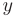 
из третьего уравнения. Для этого умножим вторую строк}’ матрицы на коэффициент —2 и почленно сложим полученную строку с третьей строкой расширенной матрицы:
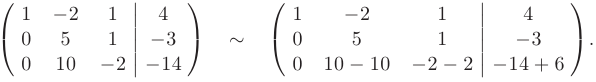
В результате получим эквивалентную исходной систему уравнений треугольного вида
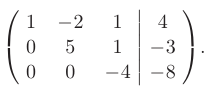
Обратный ход метода Гаусса. Найдем решение исходной системы, используя структуру полученной матрицы.
Из последнего уравнения найдем значение неизвестной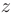 
:
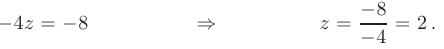
Подставляя найденное значение 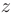во второе уравнение, найдем значение неизвестной :
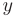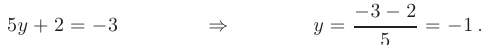
Наконец, подставляя найденные значения 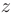и 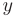в первое уравнение, найдем значение неизвестной 
:
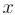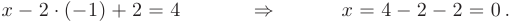
Так как найденное решение совпадает с предыдущими решениями, полученными в примерах 1.1 и 1.2 матричным методом и методом Крамера, то дополнительная проверка не требуется.
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:
| Определитель матрицы в математике |
| Обратная матрица в математике |
| Ранг матрицы в математике |
| Системы линейных уравнений m*n в математике |
