Если какие-либо уравнения или неравенства объединены фигурной скобкой в систему, то предполагается, что они должны быть выполнены одновременно, т.е. решениями системы могут быть только такие значения неизвестных, которые удовлетворяют всем уравнениям и неравенствам, входящим в систему.
Если система уравнений или неравенств имеет решения, то говорят, что она совместна, если она решений не имеет, то — несовместна.
Системы называются равносильными, если множества их решений совпадают. Основу решения системы составляют равносильные преобразования входящих в нее уравнений и неравенств. Поскольку система включает, как правило, не одну неизвестную величину, а две, три и, возможно, больше, то для исключения неизвестных и приведения системы к уравнениям и неравенствам с одной неизвестной используют такой прием как подстановка. Если из одного уравнения можно выразить одну неизвестную через другую, а затем подставить ее в другое уравнение, то это хороший способ решения, нужно только помнить об ограничениях. Однако это нелегко сделать сразу, требуются дополнительные преобразования.
Можно складывать и вычитать уравнения системы с целью исключения одной из неизвестных. Решение системы записывается следующим образом: если в системе две неизвестных х и у, то (х; у), если три неизвестных х, у, z, то (х; у; z) и т. п. В системах, так же как и в уравнениях, используются разложение на множители, замена переменных.
Умение решать системы важно при решении текстовых задач и часто является наиболее трудоемкой частью решения.
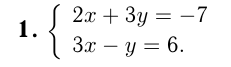
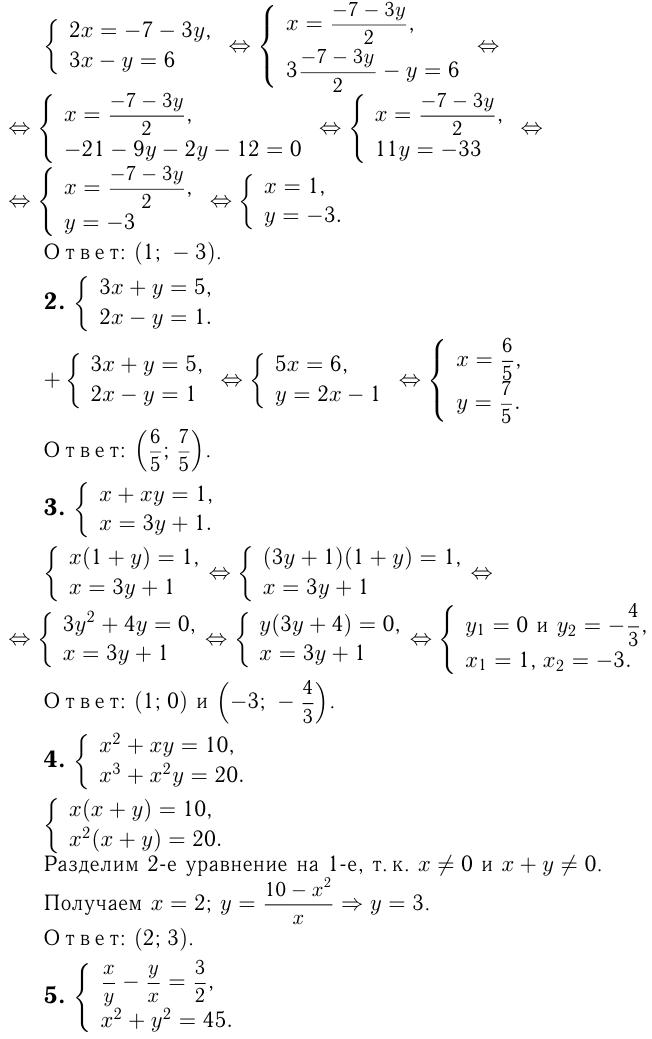
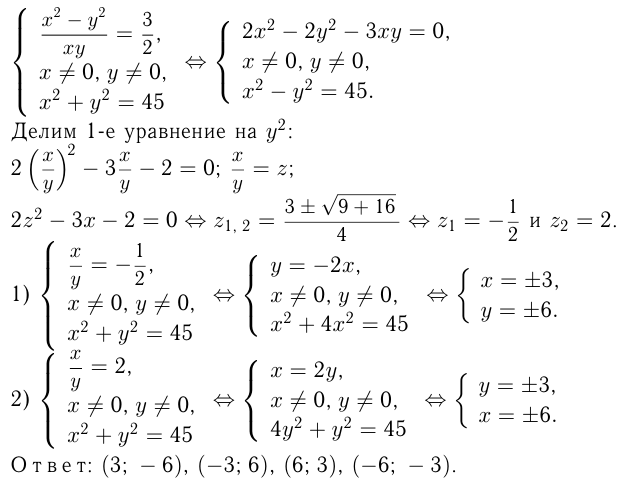
Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Решение тригонометрических неравенств |
| Решение задач на «Числовые оценки» |
| Решение систем уравнений и неравенств |
| Решение задач на проценты по математике |
