Оглавление:



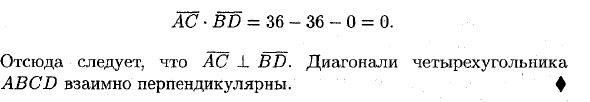
Скалярное произведение векторов и его свойства
- Вектор и его скалярная работа характеристическая Скалярное произведение двух ненулевых векторов a и b представляет собой число, равное произведению длины и косинуса этих векторов. Угол между ними. Обозначается ab, a-b (или (a, &)). Поэтому по определению a- b = | a | • \ b \ -cozy), (1) pr ^ a ° где (p = (a, 5). Выражение (1) может быть в другом формате. | a | cos = pr ^ o и | b | cos ip = npff B Потому что есть ab = | a | • pr5 b = \ b \ • npjja, (2)
Скалярные свойства продукта 1. Скалярное произведение имеет свойство перемещения ab = ba. ■ 4 ab = | a | • \ b \ • cos (a, S) и ba = | 6 | • | a | • cos (6, a). А поскольку | a | • = = \ b \ • | a |, произведение числа на (a, b) = (6, a), то ab = ba. ► 2. Скалярные произведения имеют комбинированные свойства для скалярных коэффициентов: (Aa) • b = A (ab). <(Aa) 6 = \ b \ • pr £ Aa = A • | 6 | • pr ^ a = A (a6). ►
То есть скалярное произведение двух векторов равно одному модулю, умноженному на проекцию другой оси, и соответствует первому вектору. Людмила Фирмаль
Скалярное произведение обладает свойством распределения a (b + c) = ab + ac. <4 a (b + c) = | a | -pr5 (6 + c) = | a | — (np55 + np5c) = | a | pr5b + | a |; Я 4. Скалярный квадрат вектора равен квадрату его длины: a2 = | ar. <a2 = a • a = | a | • | a | cosO = | a | • \ a \ = | a | 2. ►Около -2 т2 г2. В частности, r = j-k = 1. Если вектор a является скалярным квадратом и корень извлечен, его модуль | a |, то есть Vd? Получается. = | a | (n / i <φa). Пример: Найти длину вектора c = 3a-4b, если | a | = 2, \ b \ = 3 (A, b) = §. + = V? = (Za-46) 2 = yj9a2 ~ 24ab + 1bE2 = = ^ 9-4-24- 2-3 • i + 16-9 = v / 108 = 6l / 3. ♦ 5
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Если векторы ai, b (отличные от нуля) перпендикулярны друг другу, их скалярное произведение равно нулю. То есть a 1 6, ab = 0. Обратное также верно: ab = 0 и Φ0 ^ 5, a 1 6. Как насчет тебя? = (A, 5) = тогда cos (p = cos ~ = 0. ab- \ a \ -16 | • 0 = 0. Если a-5 = 0 и | a | φ0, \ b \ φ0, то cos (a, 5) = 0. Следовательно, tp = (a, b) = 90 °, т.е. a _L b. В частности: я •] -] — к = к-г = 0. ►
Пример: вершина A (-4; -4; 4), B (-3; 2; 2), C (2; 5; 1), £> (3; -2; Докажи диагонали) перпендикулярно друг другу. ♦ Построить векторы AC и BD по диагонали заданного четырехугольника. AS- (6; 9; -3) и BD = (6; -4; 0). Найти скалярное произведение этих векторов. AC • BD = 36-36 до 0 = 0. Результат AC -L BD.
Диагонали четырехугольника ABCD перпендикулярны друг другу. Людмила Фирмаль
