Слабые разрывы. Характеристики уравнений газовой динамики

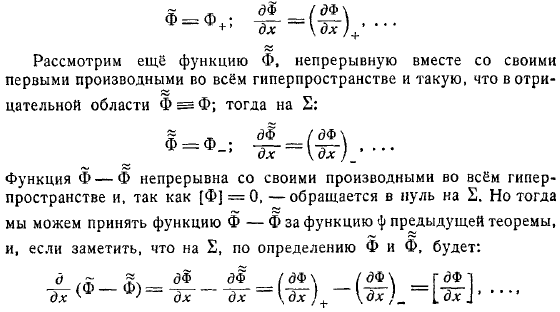
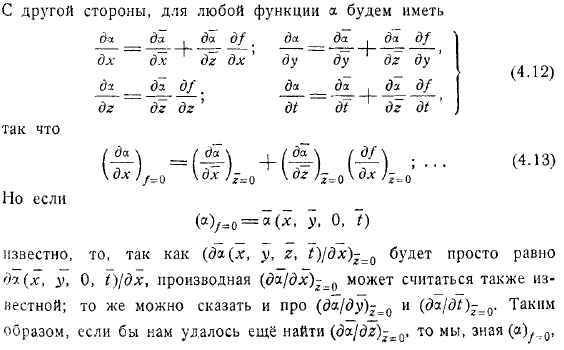
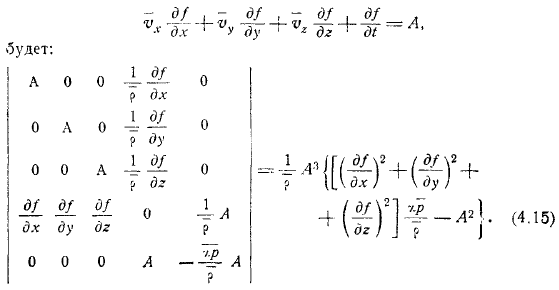
Слабые разрывы. Характеристики уравнений газовой динамики

Само существование сильных разрывов в решение задач по гидромеханике не накладывало ограничений на скачки гидродинамических элементов, и только необходимость удовлетворять уравнениям приводила к установлению соотношений. Напротив, в случае слабых разрывов необходимо связывать скачки этих дифференцирований с определенными условиями, обусловленными самим фактом существования разрыва производной, который возникает вдоль деформации и перемешивания многообразия, но всегда остается на одной поверхности. Последняя является результатом геометрической или кинематической картины движения, которая выводится совершенно независимо от уравнений гидродинамики.

Эти условия называются «условиями тождества» и «кинезиологической совместности». Для уравнений газовой динамики в дифференциальной форме и их получения предполагается, что функция непрерывна на всем пространстве, занимаемом жидкостью, но все первые производные будут разрывными на поверхности с уравнением). Можно говорить о мерном пространстве, внутри которого уже изображена неподвижная гиперповерхность.

• Теперь предположим, что у нас есть непрерывная функция с производными от независимых переменных, и что-то вроде этого на гиперповерхности.
• Затем, вдоль гиперповерхности. И разница берется по этой поверхности.

Но здесь, для уравнения. Людмила Фирмаль

Это единственное условие, накладываемое на разность координат вдоль поверхности. Если сравнивать, то во всех точках поверхности разрыва, в любой точке. Где определены функции координат и времени.

Далее рассмотрим непрерывную функцию над целым. Он имеет гиперпространство и непрерывную первую производную по координатам и времени. Эта функция идентична функции только в положительной области.

• Тогда на поверхности. Также рассмотрим такую функцию, которая непрерывна с первой производной во всем гиперпространстве и является отрицательной областью.
• После этого. Эта функция непрерывна со своей производной во всем гиперпространстве, и поэтому.

Можно взять функцию от функции предыдущей теоремы. И если вы заметите, что по определению это так. Мы можем написать. Что еще можно написать вот так. Термины и суть обсуждаемых условий совместимости-они указывают на то, что достаточно указать только функцию, чтобы определить разрыв всех производных.

Также достаточно знать деление на. Людмила Фирмаль

Также достаточно знать деление на. Например, если производная порядка имеет разрыв, равный нулю, то все производные порядка непрерывны. Формулы для деления и умножение на где — единичный нормальный вектор, вдоль которого проходит скорость поверхности слабого зазора.

Кроме кинематических условий, необходимо подчинить разрыв производной различных гидродинамических элементов динамическим условиям. Это связано с тем, что эти элементы должны удовлетворять гидродинамическим уравнениям отдельно в положительной и отрицательной областях. Предполагая, что они являются смежными, вы могли бы написать.

Наше уравнение не содержит производных более высокого порядка, чем первое. Если вы присваиваете знак плюс всем производным раз, присваиваете знак минус друг другу в другое время и вычитаете полученные уравнения друг из друга, вы получаете отношение. При использовании он выглядит так.

Есть вектор с компонентами. Сбор членов, у нас есть. Величин удовлетворяют однородным уравнениям. Для существования ненулевого значения определитель системы должен быть равен. Проще всего получить это условие, умножив первое уравнение на скаляр и вставив выражение из левой части уравнения вместо этого.

Затем получать. Согласно последнему первое из этих уравнений соответствует стационарному случаю разрыва теоремы Цемплена . Уравнение указывает, что скорость распространения нестационарного разрыва производной всегда равна.

Это значение называется скоростью звука. Мы говорили о скорости распространения слабой поверхности разрушения первой производной. Скорость распространения слабого разрыва (то есть разрыва производной любой степени) обозначается как.

Напротив, как вы сразу видите, скорость звука и скорость его мощного прерывания никак не связаны. Здесь мы покажем, как слабый зазор связан со свойствами системы уравнений газовой динамики. Последняя представляет собой систему из уравнений в частных производных порядка относительно независимых переменных, содержащих неизвестных функций.

Коши, в чем проблема? Наш случай сформулирован следующим образом. О гиперповерхностях с уравнениями все значения функции являются. Необходимо найти непрерывную и единственную функцию, которая будет удовлетворять уравнению и ориентировать его.

И заданная система ценностей. Напомним, что доказательство теоремы существования единственного решения задачи Коши обусловлено возможностью определения значений всех производных всех целевых функций в. To чтобы лучше понять процесс определения этих производных применительно к системе, мы будем выглядеть так, заменив независимые переменные.

Для этих новых переменных уравнения гиперповерхности принимают простую форму. С другой стороны, для функции. Как это. Но если известно, что производные также можно считать известными, так как они просто равны. То же самое можно сказать.

Поэтому, если вы все еще можете найти, знайте. Вы сможете рассчитать. Есть функций. Поэтому необходимо найти производных. Найти их. Используйте уравнений для записи в новую переменную. Есть следующие (мы описываем только термины, которые содержат дифференциацию относительно).

Производные могут быть найдены из этого алгебраического уравнения только в том случае, если определитель не равен нулю. Этот определитель, если мы указываем гиперповерхность ориентируется, функции, определенные на ней, как бы гасятся, система допускает только бесконечное. Для того, чтобы эти решения оставались конечными, в то же время необходимо требовать исчезновения всех детерминант, составленных путем последовательного введения соответствующей части в столбец детерминант.

В этом случае многообразие называется характеристическим многообразием (характеристической гиперповерхностью) или просто характеристикой. Обратите внимание, что при вычислении старшей производной необходимо снова обработать только определитель. Поэтому, если задача Коши имеет характерную поверхность, если существует решение задачи Коши, то оно не может быть уникальным.

Это означает, что может быть разных решения, которые принимают одни и те же значения, но их производные уже различны. Таким образом, может показаться, что с разных сторон движения действует разный закон, но в гидродинамических элементах обоих движений (но не их производных) он оказывается совпадающим. Однако в этом случае движущаяся поверхность называется слабой.

Факт, нетрудно проверить, что условие, равное нулю, соответствует из. To для этого достаточно ввести характеристику «скорость распространения». И заметьте это. Что определитель равен нулю. Вы можете вернуться к предыдущему шагу.

Таким образом, можно видеть, что движущиеся поверхности слабых разрывов и характерные многообразия системы идентичны. Всегда ли можно говорить о характерных разновидностях? Они всегда действительны? Если вы хотите отказаться от дела, о характеристиках (опустите линию над гидродинамическими элементами), где то же, что и раньше.

Скорость движения. В случае неустойчивости уравнение, очевидно, может найти реальную функцию в любом случае. А наличие последних, в общем плане, не накладывает никаких ограничений на гидродинамические элементы.

Однако предположим, что вы имеете дело со стабильным движением. Здесь естественно предположить, что разрывы являются стационарными в. Другими словами, предполагается, что скорость перемещения (а не скорость распространения) равна нулю.

Тогда он находится на прерывистой поверхности над. Здесь установившееся движение жидкости таково, что скорость во всех местах меньше локальной скорости звука. В этом случае проекция скорости жидкости на нормаль поверхности всегда будет малой, независимо от того, какая поверхность проходит через определенную точку, и везде не будет равенства.

Наоборот, жидкость движется. Тогда у вас есть поверхность, которая проходит через такое, что проекции скорости на нормали этих поверхностей точно равны. Из этого вытекает очень важный результат. Если жидкость движется в стационарном (установившемся движении), а то и везде-в дозвуковом, то здесь не может быть реального характеристического многообразия.

Наоборот, если жидкость движется со сверхзвуковой скоростью, то всегда можно построить реальные характеристики. Мы видим, что переходы скорости звука играют очень важную роль в стационарном движении, изменяя вид дифференциального уравнения движения (от дозвукового эллипсоида к гиперболе сверхзвуковой скорости). Наличие реальных характеристик на сверхзвуковых скоростях значительно облегчает решение задачи движения.

Здесь вы можете разработать эффективное графическое решение. Это можно узнать в нужном месте. Назад, если есть сильный разрыв. Вот некоторые общие теоремы, связанные с доказательством.