













- Теперь перейдем к рассмотрению газов по статистике Ферми в общем случае. Это связано с тем, что они не ограничиваются низкими температурами, и происходит их»денатурация».Мы будем использовать модель газа как before. In в частности, он не учитывает взаимодействие между частицами и выводит подходящее соотношение для любой температуры. Состояние нашей системы-Энергия 11,₂, e], … состояние частиц в количестве ₍, гг, гг,>, … полностью определяется установкой следующих параметров вероятность выполнения этого условия согласно (49.1) равна ИФЛ » л «п«…- «1′ -»/, О(п » l «l» …)、 Где все n » 1 Для 0 = 1 и не менее 1 l *> 0 = 0 для 1. E = 2 — энергия системы.
Свободная энергия ’ K, как всегда, определяется из условия нормализации вероятности и может быть выражена в сумме состояний 2. Два (51.1) Среднее число частиц в одном состоянии, например, в первом состоянии, (51.2) Как и в Формуле (51.1), для обобщения здесь нужны возможные состояния системы, то есть все состояния, в которых значения всех эта равны 0 и 1.So, O H,=£1. Потому что, общее число частиц постоянно、 Правильно. (51.3) При суммировании необходимо получить только сумму чисел A |и выполнить это условие. Очевидно, что вычисление среднего числа частиц n сводится к вычислению полного состояния 2.In факт, настройка=■ Мы получаем Поэтому достаточно рассчитать сумму состояний.
Зная это, можно, как всегда, определить свободную энергию t — 1N r, а, следовательно, определить термодинамические величины всего. При расчете и возникают математические трудности, которые связаны с необходимостью учитывать при суммировании инвариантные условия числа частиц (51.3). чтобы избежать этой трудности, выполните this. As обычно, если бот показывает m = ri mh⁴0 (m-целое число), то значение равно единице、 Тогда вы, очевидно, можете написать 2 р= В настоящее время сумма уже распространилась на все возможные n = 0,1, без учета условия(51.3).Поскольку эти условия δnot> 2″, условие, что это условие не выполняется, исчезает. _and = 0.
Размер bapping можно описать как специфический анализ. Expression. In другими словами, это легко проверить с помощью простой интеграции Разгребая его Ю. Г.] «» ‘» ’ ¿Ф-t₀; = Uvhrr 5г(2Р * — ЛГ)ч.) л Вместо Выражение выражения 7 -¿•2£ ’£■■■ш-«»¿Ф.» Путем изменения порядка интеграции Итого Во всех отношениях Сложение, n, −0.1(а теперь По тому, что было сказано, сумма n о разных n Независимо 1>от другого), получаем Но… Л(1 + 3 * эф)-1Н(1 + 7.6 **)].
Таким образом, 2-это 2⁼YG Uehr (- lg ₽+21п0 +¿ ф — (₽1-5) Если общее число частиц в системе очень велико, но концентрация S / V удерживает конечное значение, то вас интересует величина 2.So, достаточно найти приближенную асимптоту большого N, а не точное значение интеграла (51.5).Заметим, что при фиксированной концентрации YY сумма 2 1n (1 +е* e’f) возрастает пропорционально N. Это связано с тем, что энергетический уровень eв, содержащийся в Формуле g\=, зависит от размера сосуда V = D. [ср.
Формула (47.7) 1, следовательно, для данной концентрации MU сумма 21p (1 + 9le’f) зависит от N. Чтобы установить форму этой зависимости, мы поместим эту сумму с Интегралом. 2 w(1 + — I ’и(1 + * c. Где¿s (e) — число квантовых состояний частицы (47.9> интервал (e, e + (e).Если нет внешнего поля, то = VUe, так как это r 1b, эта сумма равна И если концентрация фиксирована, то сумма проблем фактически пропорциональна N.
Нетрудно заметить, что эта пропорциональность возникает при наличии внешнего поля. Таким образом, форма 2 является (51.6> Для данной концентрации эта функция не зависит от Λ.Для интегралов(51.6) можно применить теорему к асимптотическим значениям*интеграла, доказанную в конце этого раздела.
Написано stra — p » — маршрут равен Вплоть до того, что отношение к точкам маркера увеличивается с N Уравнение u?(φ0)= 0 Или уравнение (51.6 собой) (51.7) tde-это уравнение имеет 1 допустимое решение 5.Действительно, для e> 0 вперед,£ — ► — co 2 е («*- п /э ₁ 〜lg_₊’» +°°; Дериват Всегда положительный. Следовательно、 1B r _ x «S-m» (X) — — — B — +£и 0 +(S-8) Кроме того, ξ должно быть найдено из условия(51.7). Используя формулу (51.4), находим среднее число частиц в k-ом состоянии. n * = d » ■•в этом случае необходимо различать и так, учитывая, что это зависит от Н. Мощность(51.6 собой) Но я принимаю это.
Это выражение для»распределения Ферми«.Замените классическое распределение Максвелла-Больцмана, рассматривая принцип Паули. Далее(51.7), по-видимому, просто выражают ^nₖ= Н Свободная энергия нашего газа г = -einz = ^ −42 |ⁿi1+е⁽C_e*⁾ / э- ⁵11⁰> Номер частицы N. In в данном случае это получается без добавления к термину-b1nr, в зависимости от N. Это связано с необходимостью сделать в классической теории (§ 13) Для получения указанной пропорциональности N [30]. Используя (51.10) является корнем уравнения (51.7) и может легко выявить термодинамические последствия температуры и концентрации электронов зависимых величин£. (51.7) сокращает последние 2 срока.
(51.11) Другими словами,£ — это химический потенциал электрона. Из распределения Ферми, созданного в выводе следующим образом、 То есть, если по формуле (51.9) энергия системы равна энергии отдельных частиц, то есть если она учтена, то предположение всегда справедливо. Там может быть внешнее силовое поле. Поэтому это выражение справедливо при тех же предположениях, что и выражение Максвелла-Больцмана.
В соответствии со средним показателем Частица с определенным состоянием равной энергии И классическое (то есть не учитывающее принцип Паули) представление N на дискретных энергетических уровнях можно описать следующим образом: Н = const и■Е _,/ е-е т, _, > / е (51.12) Если константа равна «1 / в». Если значение энергии е велико (для знаменателя (51.9) единица может быть проигнорирована по сравнению с экспоненциальной функцией), то отверстия для распределения (51.9) и (51.12) 20 на рисунке 5 примерно одинаковы (для правой Кривой 2).Если значения малы, то эти законы совершенно другие(левая кривая 2). кривая 1).
В случае вырождения, то есть если она достаточно мала, то, как известно, статистика Ферми дает прямоугольный график; n-1 — это b 6, а n = 0 — e>£. —(ЛЗ)- — — (ЛК) При более высокой температуре (0₂) переход от части кривой, почти параллельной горизонтальной оси, к экспоненциальному уменьшению происходит при значении e = E. Это связано с тем, что при 5 экспоненциальное выражение знаменателя меньше 1, а при его уменьшении e приближается к нулю. если e больше 5 и даже больше, то экспоненциальная функция вскоре будет больше 1, а знаменатель можно заменить на e|, _c,/ c.
- Низкая температура (63 очень резкая для перехода, поэтому в 6-* 0 кривая будет представлять собой прямоугольный график(область денатурации).Из этого видно, что высший уровень эперги, который заполнен 5 ″ вырождением, введенным в§ 49, равен 6 = 0 и 5:£、> =£(0)。 При очень высоких температурах 5 будет отрицательным, что указывает на то, что он растет бесконечно в абсолютном values. In кроме того, функция распределения Ферми, то есть формула (51.9) для среднего числа n частиц, превращается в классическую формулу Максвелла (51.12).при этом все свойства Ферми-газа при высоких температурах совпадают с свойствами газа, полученными из классической статистики.
Мы проанализируем частный случай при отсутствии внешних сил (за исключением взаимодействия со стенкой). в этом случае, согласно (47.9)17Ae)= Vur’Pie, B-2,,, m, g / l2 L\, я свободен — «п-tr11n ⁽* + ’, м *)51.13> И определить 5 к форме в условии (51.7) (51.14)) среднее число частиц с энергией между Е и Е + Е н(е)м(е)=(51.15> Найти уравнение состояния gas. To для этого мы выделяем P для каждого объема. ⁵ *-, ⁶ > С другой стороны, Γ является однородной функцией 1-го порядка от числа частиц N и объема V 1 см.
Используя (51.10) 1, и теорему Эйлера для однородных функций, и формулу (51.11), (51.16、 Ф-л-х-УР плутоний^ +¥>—、 Подставляя V из Формулы (51.10)、 пу = БВУ 11н (1 + е Э_э⁾/ С) Е ’ ^ Е С помощью интеграции компонентов、 Е = = 2 Так… плутоний= Принять здесь При заданном пределе интеграции он изменяется в результате、 Средняя энергия газа Средняя энергия зависит от температуры Концентрации (51.18).5-функции концентрации S / V и B, которые определяются по формуле (51.7). Найти приближенную формулу термодинамических величин при низких температурах в вырожденном состоянии regions.
To для этого преобразуем выражения (51.15) и (51.18). / В =(А (Е) РД(Е)= [С(Е)Р(Е)]₌ ₀-12 (е) н ’ (р)1Р = =—у ву е’/!Ж (е) ¿8,(51.19) £= WuSp (e)e’1ye = = VU _ 2. дю Е В ’(Е)¿Е = — вю у ПЗВ’(е)л. (51.20) Величина r ’(e) при низких температурах существенно отличается от пули только в окрестности величины e-e(0).Где R) падает от единицы до нуля при малом 0.So, поставьте e — + + » 0 и расширьте E11 из (51.19) и e⁵⁵1 (51.20) силой И.
Вот такая пандемия ^ е |> н ’ (е)1е = [(£+и0)₽Ди = Где Р — 3/2 или 5/2. Мы будем рассматривать его ■ ^ 〜(7 + 1?) Это четная функция. И затем… Интеграция Мы получаем 5лг. если β= 0, то первое уравнение:£= {;, =(2ВУ / за0_г/>.Решите уравнение о £(51.22) и найдите до степени член(в/£)!) 4. * ■ + ’) ■ Нижний предел — / / можно может быть заменен ошибкой порядка E на ’/ £ / в ’ (’/£/в’). Будем рассматривать дальше. Здесь.£,=(Зл72ву)!
Деление (51.23) на 1£(51.24)、 с = б (51.24) Получить в экспресс шаг точности = * ■ + 4 (51.25) С=, Найти теплоемкость отсюда тг№кт _2″. (51.26) Если температура очень низка сравненная к вырожденной температуре, то теплоемкость будет очень small. It это около KT / b раз Это меньше, чем обычное значение теплоемкости. Это объясняет, почему электрон при комнатной температуре увеличивает теплоемкость металла. Также обратите внимание, что он использует (51.13) и свободную энергию. Она равная. Если нет внешней силы, то энергия P равна e = p ’/ 2m.
Поэтому в этом случае можно выразить абсолютное количество движения и распределение частиц в статистике Ферми, а также¿I, что часто делается в»классической статистике P». Используя (51.15), получим уравнение для среднего числа частиц, имеющих импульс в интервале p, p + pp Это соответствует формуле Максвелла в классической статистике ¿Н (П)= п’ДП.- (51.29) график функции ip / yr показан на рисунке. 21 (сплошная кривая по формуле (51.28), кривая по пунктирной линии по формуле (51.29).Энергия E — £здесь соответствует импульсу P = 12m ^и переход от параболы пропорционален (он убывает экспоненциально пропорционально кривой P’>).Здесь случай вырождается рис.
21. Здесь, при p = Po = V2m££, кривая разбивается на ноль. В заключение найдем асимптотическое представление интеграла (N — * ■°*) * ) Ссылка: Курант Р., Гильберт Д. методы математической физики: Пер. — 3-е издание-М.: Гостехиздат, 1951, т. I, ч. VII, 5-6, стр. Применение к интеграции, встречающейся в статистической теории, дано Фаулером и Даргиным. См. книгу: Фаулер, статистическая механика, Кембридж, 1936.
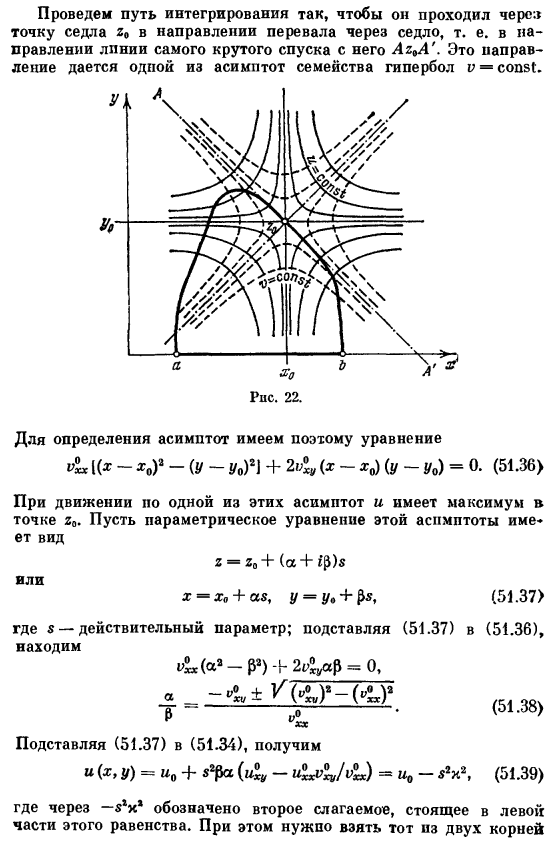
Чтобы найти асимптотическую формулу этого интеграла, который должен быть взят по определенному пути на плоскости комплексной переменной r-x + 1y (в данном случае по действительному значению r), используйте»метод прохождения».Предположим, что функции Γ ® и w (x) — u (x, y)+ u>(x, y)аналитичны в области 2 плоскости interest. To для решения этой задачи необходимо правильно деформировать путь интегрирования (как известно из теоремы Коши, значение пути интегрирования не изменяется). Если мы возьмем 2n как корень производной g ’(s)、 1-е производные NVS относительно xn y связаны между собой уравнением коппюша-Римана relationship.
It удовлетворяет действительной и мнимой части любой аналитической функции и представляет независимость производной от направления производной. (51.30)) (51.31).) В точке R, все эти первые производные равны нулю. (51.32) из-за особенностей аналитической функции в точке r, ни максимальное, ни минимальное значение функции и u V, эти функции имеют седло(если u и V перпендикулярны плоскости xy). 2-й производных, таких как ум и N、 (51.33) Получено дифференциалом из (51.31).Разверните, в ряд, близкий к r-r, рассматривая (51.32) и (51.32) u (x, y)= = «. + 4-* О) ’〜(у—хо) (У-и>) 1.
(51.34) Вторая форма здесь неопределенная (вы можете изменить знак).Это означает, что точка z является точкой на поверхности u (x, y), v(x, y).Кроме того, поверхность, на которой изображена хна в качестве функции, можно представить как гористую местность. Сечение поверхности плоскостью u = const дает на ней горизонтальную линию, а сечение i> = const дает линию самого крутого склона, поскольку по (51.31) оно перпендикулярно этим горизонтальным линиям (см. рис.22). Для определения асимптоты, следовательно, существует уравнение &К — * О)-(Г-по)* 1 + 2> ^(х-хп)(г-г «)= 0.(51.36) При движении вдоль одной из этих асимптот максимум наблюдается в точке R Chai.
So параметрическое уравнение этой асимптоты г-г+(а + 1П) с Х-Х ’+ аз, г = г. +&、 (51.37) Где » — допустимый параметр. Присвоение (51.37)- (51.36)、 «£х (a⁴ -₽’) + =о、 ₍₅₁₃₈₎ Присвоение (51.37)- (51.34)、 «(Х, г)=У±* ’*2. (51.39).) Где — * * x * обозначает 2-й член слева от этого equation. In в этом случае вам нужно взять 2 маршрута pz 0、 (51.39) за это РА (4»- Поэтому максимальное значение равно 5 = 0. (51.39) и (51.34) близки к сегменту AA, благодаря m Коэффициент e «линейный АА вблизи e⁰z» зависит от 5 как Гауссова кривая, но чем острее она становится, тем больше она становится. Поэтому, если N достаточно большой, вы можете ограничить его любым небольшим сегментом вокруг x. v.
Во время интеграции. Показано, что остальная часть Интеграла дает добавки, которые экспоненциально уменьшаются с увеличением N. поэтому、 Под знаком интеграла. Предполагаемый= Мы получаем Так… При увеличении Λ предел стремится к асимптотическому выражению.
Смотрите также:
| Статистика Ферми для случая «вырождения» газа | Идеальный газ, подчиняющийся статистике Бозе— Эйнштейна |
| Парамагнетизм электронного газа и парамагнитные свойства щелочных металлов | Броуновское движение |
