Оглавление:
Вспомните, как постепенно расширялось понятие степени. Сначала вводилось понятие степени числа с натуральным показателем n:
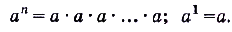
Затем рассматривались степени с целым показателем:
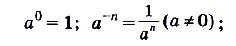
наконец — с произвольным рациональным показателем степени:
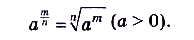
Математики часто используют также степени с произвольными действительными показателями. Множество действительных чисел состоит из чисел рациональных и иррациональных. Что такое степень с рациональным показателям, вы уже знаете. Введём понятие степени с иррациональным показателем.
Пусть
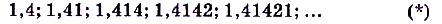
бесконечная последовательность рациональных приближений числа 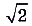 с точностью до десятых, сотых, тысячных и т. д. То есть это последовательность рациональных чисел, достаточно близко приближающихся к
с точностью до десятых, сотых, тысячных и т. д. То есть это последовательность рациональных чисел, достаточно близко приближающихся к 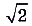 . Тогда
. Тогда
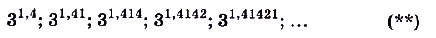
последовательность чисел (степеней с рациональными показателями), которые как угодно близко приближаются к некоторому действительному числу. Это действительное число и принято считать значением степени 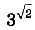 .
.
Приближённые значения (с точностью до десятых, сотых, тысячных и т. д.) для степеней 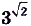 и
и 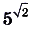 представлены в таблице, выполненной с помощью программы Excel (рис. 14)
представлены в таблице, выполненной с помощью программы Excel (рис. 14)
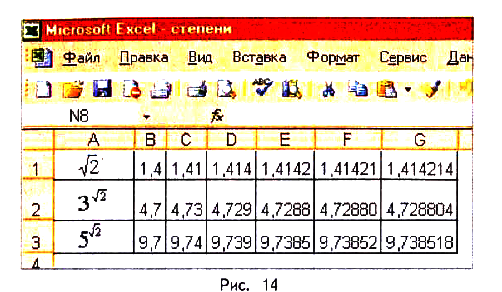
Замечание. Приведённое выше объяснение понятия степени с иррациональным показателем с точки зрения математики не совсем корректное, поскольку в нём используется нематематическое понятие «близко подходит». В математике ему соответствует понятие предел последовательности. Число а называют пределом бесконечной последовательности 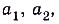
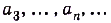 , если для любого положительного числа
, если для любого положительного числа 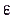 найдётся такое натуральное число
найдётся такое натуральное число 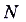 , что для всех n > N выполняется неравенство
, что для всех n > N выполняется неравенство 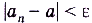 . Поэтому правильнее было бы сказать, что если пределом последовательности (*) есть число
. Поэтому правильнее было бы сказать, что если пределом последовательности (*) есть число 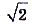 , то пределом последовательности (**) является число
, то пределом последовательности (**) является число 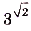 . Вообще, если а > 0 — число действительное,
. Вообще, если а > 0 — число действительное, 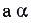 — иррациональное, то под степенью
— иррациональное, то под степенью 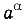 понимают предел бесконечной последовательности
понимают предел бесконечной последовательности 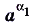
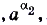
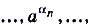 где
где 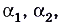
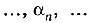 — бесконечная последовательность, пределом которой является число
— бесконечная последовательность, пределом которой является число 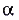 . Корректность такого определения обоснована в строгих курсах математического анализа. В § 9 будут представлены подробные сведения о границе числовой последовательности.
. Корректность такого определения обоснована в строгих курсах математического анализа. В § 9 будут представлены подробные сведения о границе числовой последовательности.
Какими бы ни были действительные числа а > 0 и 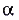 , степень
, степень 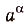 всегда имеет смысл, т. е. равна некоторому действительному числу. Для таких степеней выполняются свойства:
всегда имеет смысл, т. е. равна некоторому действительному числу. Для таких степеней выполняются свойства:
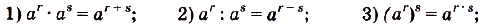
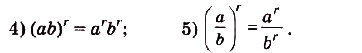
Выражения, содержащие степени с действительными показателями, можно преобразовывать так же, как выражения со степенями с рациональными показателями.
Пример:
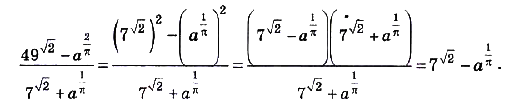
Как вы уже знаете, степени с дробными показателями рассматривают только при условии, что их основания — числа положительные. И степени с иррациональными показателями рассматривают только при условии, что основания степеней — числа положительные. А, например, выражения 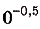 ,
, 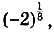
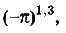
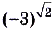 — не имеют смысла. Это записи, которые не обозначают никаких чисел. Но, если
— не имеют смысла. Это записи, которые не обозначают никаких чисел. Но, если 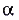 > 0 , то
> 0 , то 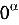 существует и
существует и 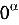
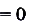
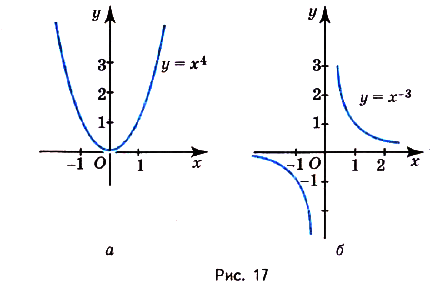
Зная только степени с рациональными показателями, вы раньше и степенные функции рассматривали не все, а только такие, показатели степеней которых были рациональными числами. Теперь понятие степенной функции можно расширить. Степенной далее будем называть функцию 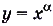 , где
, где 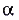 — произвольное дей-ствительное число. В частности, функции
— произвольное дей-ствительное число. В частности, функции 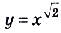 ,
, 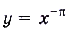 — степенные. Свойства этих функций такие же, как и свойства степенных функций с рациональными показателями степеней.
— степенные. Свойства этих функций такие же, как и свойства степенных функций с рациональными показателями степеней.
При каждом действительном 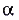 степенная функция
степенная функция 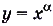 определена на промежутке
определена на промежутке 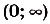 . Свойства таких функций указаны в таблице.
. Свойства таких функций указаны в таблице.

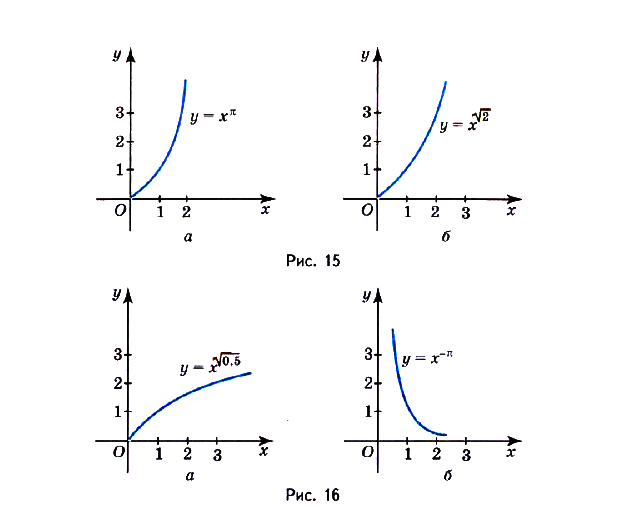
Если 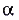 — положительное иррациональное число, функция
— положительное иррациональное число, функция 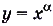 определена на промежутке
определена на промежутке 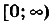 ; такое же и множество её значений. Если иррациональное число
; такое же и множество её значений. Если иррациональное число 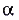 отрицательное, то областью определения и областью значений функции
отрицательное, то областью определения и областью значений функции 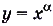 является промежуток
является промежуток 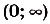 . Несколько графиков таких функций изображены на рисунках 15,16
. Несколько графиков таких функций изображены на рисунках 15,16
Для отдельных значений 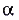 степенная функция может рассматриваться и на более широкой области определения. В частности при натуральных
степенная функция может рассматриваться и на более широкой области определения. В частности при натуральных 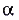 она определена на R (рис. 17, а), а при целых отрицательных — на множестве
она определена на R (рис. 17, а), а при целых отрицательных — на множестве 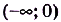
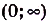 (рис. 17,6). В этих случаях при чётных значениях
(рис. 17,6). В этих случаях при чётных значениях 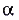 функция
функция 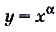 чётная, а при нечётных
чётная, а при нечётных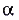 — нечётная.
— нечётная.
Примеры с решением
Пример №1
Проходит ли график функции 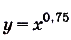 через точку М (16; 8)?
через точку М (16; 8)?
Решение:
Если 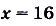 , то
, то 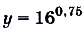
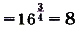 .
.
Ответ. Проходит.
Пример №2
Известно, что график функции 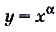 проходит через точку
проходит через точку 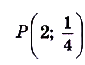 . Чему равно
. Чему равно 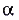 ?
?
Решение:
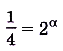 ,
, 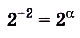 , отсюда
, отсюда 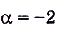 . Ответ. -2.
. Ответ. -2.
Пример №3
Упростите выражение 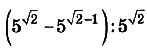 .
.
Решение:
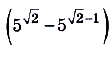
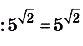
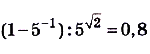 .
.
Ответ. 0,8.
Пример №4
Сравните числа: а) 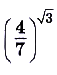 и
и 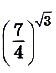 б)
б) 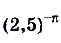 и
и 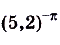
Решение:
а) Функция 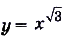
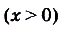 — возрастающая, так как
— возрастающая, так как 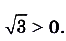 Поскольку
Поскольку 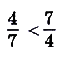 , то
, то 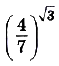
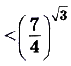 .
.
б) Функция 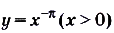 — убывающая, так как
— убывающая, так как 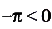 , поэтому
, поэтому 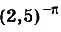
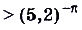 .
.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Функции и их основные свойства |
| Предел последовательности |
| Показательные функции |
| Первообразная и интеграл |
